LeetCode42:Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example, 
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

这道题很久之前做过，现在又碰到了，很快就解了出来。

解法一

两次遍历的解法。

先进行一次遍历，找到最高的那个元素的下标，然后进行第二次遍历，第二次遍历又分成从左到最大值的遍历和从右到最大值的遍历。

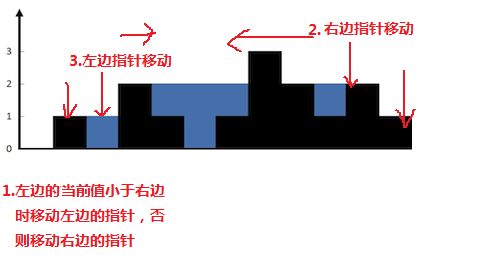
从左边开始遍历时使用一个变量来记录从左边开始的极大值，如果当前遍历的元素小于这个极大值，它们之前的差值是当前点可以容纳的水量，如果当前元素大于这个极大值，那么更新极大值。右边的遍历方式类似。如下图：

runtime:8ms

class Solution {
public:
    int trap(vector<int>& height) {
        int maxPos=0;
        int maxHeight=0;
        int length=height.size();
        for(int i=0;i<length;i++)
        {
            if(height[i]>maxHeight)
            {
                maxHeight=height[i];
                maxPos=i;
            }
        }
        int result=0;
        int leftHeight=0;
        for(int i=0;i<maxPos;i++)
        {
            if(height[i]>leftHeight)
            {
                leftHeight=height[i];
            }
            else
            {
                result+=leftHeight-height[i];
            }
        }
        int rightHeight=0;
        for(int i=length-1;i>maxPos;i--)
        {
            if(height[i]>rightHeight)
            {
                rightHeight=height[i];
            }
            else
            {
                result+=rightHeight-height[i];
            }
        }
        return result;
    }
};

解法二

第二种解法是使用一次遍历的解法。

上面的解法之所以要遍历两次，是为了寻找最大值，这样能够保证极大值与当前值的差值是能容纳的水量，但是其实可以不用求出最大值而是使用左边和右边当前值的最大值。如果左边的当前值较大，那么遍历右边，如果右边的当前值较大，遍历左边，这样就能保证极大值与当前值的差值是能容纳的水量。

runtime:8ms

     int trap(vector<int>& height) {
        int length=height.size();
        int result=0;
        int leftPos=0;
        int rightPos=length-1;
        int leftMax=0;
        int rightMax=0;
        while(leftPos<rightPos)
        {
            if(height[leftPos]<height[rightPos])
            {
                if(height[leftPos]<leftMax)
                    result+=leftMax-height[leftPos];
                else
                    leftMax=height[leftPos];
                leftPos++;
            }
            else
            {
                if(height[rightPos]<rightMax)
                    result+=rightMax-height[rightPos];
                else
                    rightMax=height[rightPos];
                rightPos--;
            }
        }
        return result;
         
     }