Burst Balloons

题目描述：

Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.

Find the maximum coins you can collect by bursting the balloons wisely.

Note:
(1) You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
(2) 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

Example:

Given [3, 1, 5, 8]

Return 167

    nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
   coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

我先自己写了一个回溯算法，超时：

public int maxCoins(int[] nums) {
    int[] leftIndexs=new int[nums.length];
    int[] rightIndexs=new int[nums.length];
    for(int i=0;i<leftIndexs.length;i++){
    	leftIndexs[i]=i-1;
    	rightIndexs[i]=i+1;
    }
    return getMaxCoins(nums, leftIndexs, rightIndexs);
}

public int getMaxCoins(int[] nums,int[] leftIndexs,int[] rightIndexs){
	int max=0;
	boolean visited=false;
	for(int i=0;i<nums.length;i++){
		if(nums[i]!=Integer.MAX_VALUE){
			visited=true;
			int leftvalue=leftIndexs[i]==-1?1:nums[leftIndexs[i]];
			int rightvalue=rightIndexs[i]==nums.length?1:nums[rightIndexs[i]];
			int num=nums[i]*leftvalue*rightvalue;
			int rightLeftIndex=0,leftRightIndex=0;
			if(rightIndexs[i]<nums.length){
				rightLeftIndex=leftIndexs[rightIndexs[i]];
				leftIndexs[rightIndexs[i]]=leftIndexs[i];
			}
			if(leftIndexs[i]>=0){
				leftRightIndex=rightIndexs[leftIndexs[i]];
				rightIndexs[leftIndexs[i]]=rightIndexs[i];
			}
			int value=nums[i];
			nums[i]=Integer.MAX_VALUE;
			num+=getMaxCoins(nums, leftIndexs, rightIndexs);
			max=num>max?num:max;
			if(rightIndexs[i]<nums.length){
				leftIndexs[rightIndexs[i]]=rightLeftIndex;
			}
			if(leftIndexs[i]>=0){
				rightIndexs[leftIndexs[i]]=leftRightIndex;
			}
			nums[i]=value;
		}
	}
	if(!visited)
		return 0;
	return max;
}

后来将这个算法优化了一点，将之前没有计算过的计算一遍，然后记录下来，当再次碰到的时候直接读取。

虽然性能上有所提高，但是还是超时了：

public class Solution {
   public int maxCoins(int[] nums) {
	    int[] leftIndexs=new int[nums.length];
	    int[] rightIndexs=new int[nums.length];
	    for(int i=0;i<leftIndexs.length;i++){
	    	leftIndexs[i]=i-1;
	    	rightIndexs[i]=i+1;
	    }
	    int[] dp=new int[(int)Math.pow(2, nums.length)];
	    Arrays.fill(dp, -1);
	    return getMaxCoins(nums, leftIndexs, rightIndexs, 0, dp);
	}
	
	public int getMaxCoins(int[] nums,int[] leftIndexs,int[] rightIndexs,int key,int[] dp){
		if(dp[key]!=-1)
			return dp[key];
		int max=0;
		for(int i=0;i<nums.length;i++){
			if(nums[i]!=Integer.MAX_VALUE){
				int leftvalue=leftIndexs[i]==-1?1:nums[leftIndexs[i]];
				int rightvalue=rightIndexs[i]==nums.length?1:nums[rightIndexs[i]];
				int num=nums[i]*leftvalue*rightvalue;
				int rightLeftIndex=0,leftRightIndex=0;
				if(rightIndexs[i]<nums.length){
					rightLeftIndex=leftIndexs[rightIndexs[i]];
					leftIndexs[rightIndexs[i]]=leftIndexs[i];
				}
				if(leftIndexs[i]>=0){
					leftRightIndex=rightIndexs[leftIndexs[i]];
					rightIndexs[leftIndexs[i]]=rightIndexs[i];
				}
				int value=nums[i];
				nums[i]=Integer.MAX_VALUE;
				num+=getMaxCoins(nums, leftIndexs, rightIndexs, (int)(key+Math.pow(2, i)), dp);
				max=num>max?num:max;
				if(rightIndexs[i]<nums.length){
					leftIndexs[rightIndexs[i]]=rightLeftIndex;
				}
				if(leftIndexs[i]>=0){
					rightIndexs[leftIndexs[i]]=leftRightIndex;
				}
				nums[i]=value;
			}
		}
		dp[key]=max;
		return max;
	}
}

正确解法是：

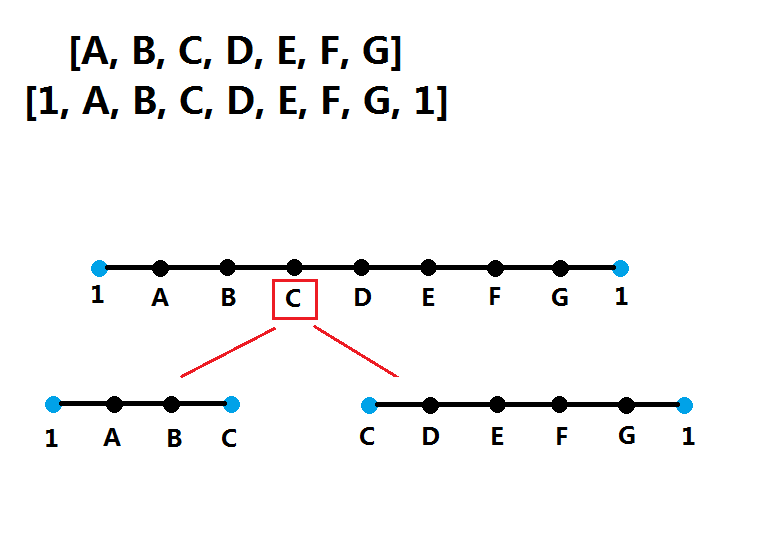
举例来说，数组[A,B,C,D,E,F,G]，代表任意数字。

首先去掉所有的零，在头和尾加上两个1表示边界。

最外层循环就是从A到G，代表了最后一个踩的气球。

假设遍历到C这个点，最后要踩C，那么C的值是固定的，为1 * C * 1。

然后考虑两边，左边的是以1和C为边界，求出最大值，右边是以C和1为边界求最大值，如图所示。

递归求出结果。

还要开一个二维数组记录中间结果提高效率。

 

最后的剩下一个气球为m的时候，可以获得的分数为 nums[-1]*nums[m]*nums[n].

那么介于l, r之间的m, 有 dp[l][r] = max(dp[l][r], dp[l][m] + nums[l] * nums[m] * nums[r]  + dp[m][r]).

l与r的跨度k从2开始逐渐增大；

三重循环依次枚举范围跨度k, 左边界l, 中点m, 右边界r = l + k

Java D&C with Memoization

public int maxCoins(int[] iNums) {
    int[] nums = new int[iNums.length + 2];
    int n = 1;
    for (int x : iNums) if (x > 0) nums[n++] = x;
    nums[0] = nums[n++] = 1;


    int[][] memo = new int[n][n];
    return burst(memo, nums, 0, n - 1);
}

public int burst(int[][] memo, int[] nums, int left, int right) {
    if (left + 1 == right) return 0;
    if (memo[left][right] > 0) return memo[left][right];
    int ans = 0;
    for (int i = left + 1; i < right; ++i)
        ans = Math.max(ans, nums[left] * nums[i] * nums[right] 
        + burst(memo, nums, left, i) + burst(memo, nums, i, right));
    memo[left][right] = ans;
    return ans;
}

Java DP

public int maxCoins(int[] iNums) {
    int[] nums = new int[iNums.length + 2];
    int n = 1;
    for (int x : iNums) if (x > 0) nums[n++] = x;
    nums[0] = nums[n++] = 1;


    int[][] dp = new int[n][n];
    for (int k = 2; k < n; ++k)
        for (int left = 0; left < n - k; ++left) {
            int right = left + k;
            for (int i = left + 1; i < right; ++i)
                dp[left][right] = Math.max(dp[left][right], 
                nums[left] * nums[i] * nums[right] + dp[left][i] + dp[i][right]);
        }

    return dp[0][n - 1];
}