最小生成树之prim算法
边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
最小生成树(MST):权值最小的生成树。
生成树和最小生成树的应用:要连通n个城市需要n-1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。
构造网的最小生成树必须解决下面两个问题:
1、尽可能选取权值小的边,但不能构成回路;
2、选取n-1条恰当的边以连通n个顶点;
MST性质:假设G=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
1.prim算法
基本思想:假设G=(V,E)是连通的,TE是G上最小生成树中边的集合。算法从U={u0}(u0∈V)、TE={}开始。重复执行下列操作:
在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE中,同时v0并入U,直到V=U为止。
此时,TE中必有n-1条边,T=(V,TE)为G的最小生成树。
Prim算法的核心:始终保持TE中的边集构成一棵生成树。
注意:prim算法适合稠密图,其时间复杂度为O(n^2),其时间复杂度与边得数目无关,而kruskal算法的时间复杂度为O(eloge)跟边的数目有关,适合稀疏图。
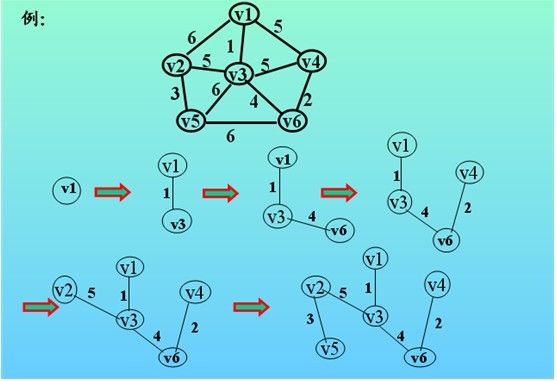
看了上面一大段文字是不是感觉有点晕啊,为了更好理解我在这里举一个例子,示例如下:
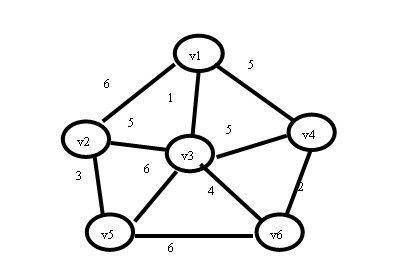
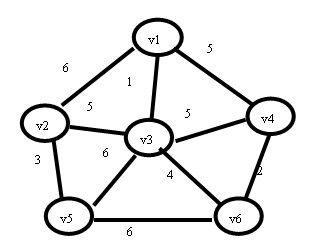
(1)图中有6个顶点v1-v6,每条边的边权值都在图上;在进行prim算法时,我先随意选择一个顶点作为起始点,当然我们一般选择v1作为起始点,好,现在我们设U集合为当前所找到最小生成树里面的顶点,TE集合为所找到的边,现在状态如下:
U={v1}; TE={};
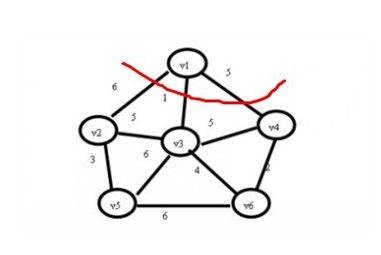
(2)现在查找一个顶点在U集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v1-v3的权值最小为1,那么将v3加入到U集合,(v1,v3)加入到TE,状态如下:
U={v1,v3}; TE={(v1,v3)};
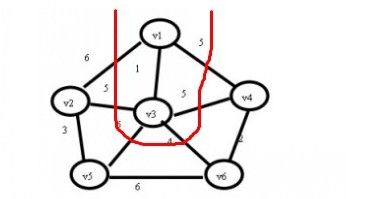
(3)继续寻找,现在状态为U={v1,v3}; TE={(v1,v3)};在与红线相交的边上查找最小值。
我们可以找到最小的权值为(v3,v6)=4,那么我们将v6加入到U集合,并将最小边加入到TE集合,那么加入后状态如下:
U={v1,v3,v6}; TE={(v1,v3),(v3,v6)}; 如此循环一下直到找到所有顶点为止。
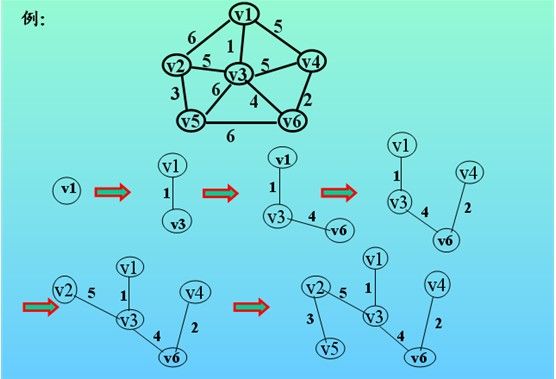
(4)下图像我们展示了全部的查找过程:
2.prim算法程序设计
(1)由于最小生成树包含每个顶点,那么顶点的选中与否就可以直接用一个数组来标记used[max_vertexes];(我们这里直接使用程序代码中的变量定义,这样也易于理解);当选中一个数组的时候那么就标记,现在就有一个问题,怎么来选择最小权值边,注意这里最小权值边是有限制的,边的一个顶点一定在已选顶点中,另一个顶点当然就是在未选顶点集合中了。我最初的一个想法就是穷搜了,就是在一个集合中选择一个顶点,来查找到另一个集合中的最小值,这样虽然很易于理解,但是很明显效率不是很高,在严蔚敏的《数据结构》上提供了一种比较好的方法来解决:设置两个辅助数组lowcost[max_vertexes]和closeset[max_vertexes],lowcost[max_vertexes]数组记录从U到V-U具有最小代价的边。对于每个顶点v∈V-U,closedge[v], closeset[max_vertexes]记录了该边依附的在U中的顶点。
注意:我们在考虑两个顶点无关联的时候设为一个infinity 1000000最大值。
说了这么多,感觉有点罗嗦,还是发扬原来的风格举一个例子来说明,示例如下:
过程如下表:顶点标号都比图中的小1,比如v1为0,v2为1,这里首先选择v1点。
|
|
Lowcost[0] |
Lowcost[1] |
Lowcost[2] |
Lowcost[3] |
Lowcost[4] |
Lowcost[5] |
U |
V-U |
| closeset |
v1,infinity |
v1,6 |
v1,1 |
v1,5 |
v1,infinity |
v1,infinity |
v1 |
v1,v2,v3,v4,v5,v6 |
从这个表格可以看到依附到v1顶点的v3的Lowcost最小为1,那么选择v3,选择了之后我们必须要更新Lowcost数组的值,因为记录从U到V-U具有最小代价的边,加入之后就会改变。这里更新Lowcost和更新closeset数组可能有点难理解,
for (k=1;k<vcount;k++)
if (!used[k]&&(G[j][k]<lowcost[k]))
{ lowcost[k]=G[j][k];
closeset[k]=j; }
}
j为我们已经选出来的顶点,如果G[j][k]<lowcost[k],则意味着最小权值边发生变化,更新该顶点的最小lowcost权值,依附的顶点肯定就是刚刚选出的顶点j,closeset[k]=j。
|
|
Lowcost[0] |
Lowcost[1] |
Lowcost[2] |
Lowcost[3] |
Lowcost[4] |
Lowcost[5] |
U |
V-U |
| closeset |
v1,infinity |
v1,6 |
v1,1 |
v1,5 |
v3,6 |
v3,4 |
v1,v3 |
v1,v2,v4,v5,v6 |
这样一直选择下去直到选出所有的顶点。
(2)上面把查找最小权值的边结束了,但是这里有一个问题,就是我们没有存储找到的边,如果要求你输出找到的边那么这个程序就需要改进了,我们刚开始的时候选取的是v1作为第一个选择的顶点,那我们设置一个father[]数组来记录每个节点的父节点,当然v1的父节点肯定没有,那么我们设置一个结束标志为-1,每次找到一个新的节点就将它的父节点设置为他依附的节点,这样就可以准确的记录边得存储了。
| 语法:prim(Graph G,int vcount,int father[]); |
|
| 参数: |
|
| G: |
图,用邻接矩阵表示 |
| vcount: |
表示图的顶点个数 |
| father[]: |
用来记录每个节点的父节点 |
| 返回值: |
null |
| 注意: |
|
|
|
常数max_vertexes为图最大节点数 |
|
|
常数infinity为无穷大 |
|
|
数组存储从0开始 |
|
|
如果下面的源程序有错请参照测试程序。 |
| 源程序: |
|
|
|
#define infinity 1000000 int closeset[max_vertexes],used[max_vertexes]; int min; /* 最短距离初始化为其他节点到1号节点的距离 */ /* 标记所有节点的依附点皆为默认的1号节点 */ /* vcount个节点至少需要vcount-1条边构成最小生成树 */ min = infinity; /* 找满足条件的最小权值边的节点k */ /* 边权值较小且不在生成树中 */ { min = lowcost[k]; j=k; } /* 发现更小的权值 */ lowcost[k]=G[j][k];/*更新最小权值*/ } |
测试程序:
测试用例:
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
5 6 6
4 6 2
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define infinity 1000000
#define max_vertexes 6
typedef int Graph[max_vertexes][max_vertexes];
void prim(Graph G,int vcount,int father[])
{
int i,j,k;
int lowcost[max_vertexes];
int closeset[max_vertexes],used[max_vertexes];
int min;
for (i=0;i<vcount;i++)
{
/* 最短距离初始化为其他节点到1号节点的距离 */
lowcost[i]=G[0][i];
/* 标记所有节点的依附点皆为默认的1号节点 */
closeset[i]=0;
used[i]=0;
father[i]=-1;
}
used[0]=1; /*第一个节点是在s集合里的*/
/* vcount个节点至少需要vcount-1条边构成最小生成树 */
for (i=1;i<=vcount-1;i++)
{
j=0;
min = infinity;
/* 找满足条件的最小权值边的节点k */
for (k=1;k<vcount;k++)
/* 边权值较小且不在生成树中 */
if ((!used[k])&&(lowcost[k]<min))
{
min = lowcost[k];
j=k;
}
father[j]=closeset[j];
printf("%d %d\n",j+1,closeset[j]+1);//打印边
used[j]=1;;//把第j个顶点并入了U中
for (k=1;k<vcount;k++)
/* 发现更小的权值 */
if (!used[k]&&(G[j][k]<lowcost[k]))
{
lowcost[k]=G[j][k];/*更新最小权值*/
closeset[k]=j;;/*记录新的依附点*/
}
}
}
int main()
{
FILE *fr;
int i,j,weight;
Graph G;
int fatheer[max_vertexes];
for(i=0; i<max_vertexes; i++)
for(j=0; j<max_vertexes; j++)
G[i][j] = infinity;
fr = fopen("prim.txt","r");
if(!fr)
{
printf("fopen failed\n");
exit(1);
}
while(fscanf(fr,"%d%d%d", &i, &j, &weight) != EOF)
{
G[i-1][j-1] = weight;
G[j-1][i-1] = weight;
}
prim(G,max_vertexes,fatheer);
return 0;
}
程序结果:
3 1
6 3
4 6
2 3
5 2
请按任意键继续. . .
http://blog.chinaunix.net/uid-25324849-id-2182922.html