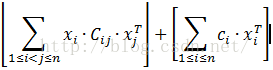指令选择器调查（6）

5.      基于图的做法

依赖图覆盖的指令选择器是目前能得到的最强大的代码生成器。通过允许输入及模式具有任意的图形状，指令选择器能够接受整个函数为输入——这被称为全局指令选择——有可能处理各种机器指令，包括硬件循环及SIMD指令。最重要的，与局限在单个基本块的基于DAG覆盖的技术相比，全局指令选择器可以在多个块间自由地移动及覆盖节点。这增加了应用复杂模式的机会，这可能导致性能提升及减少功耗。

因为大多数图覆盖方法通过应用某些通用的子图同构算法来处理模式匹配问题，我们将从简单地看几个这样的算法开始。

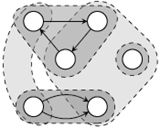
图5.1：图覆盖问题的一个例子。模式实例由虚线及包含了该模式匹配节点的阴影面积表示。

5.1.         子图同构算法

子图同构问题是检测是否可以转动、扭转或镜像任意一个图G_a，使得它成为另一个图G_b的一个子图。在这样的情形里，称G_a是G_b的一个子图同构，它已知是待定的一个NP完全问题【55】。因为在许多其他领域都能发现子图同构，大量的研究一直致力于这个问题。在本节，我们将简单看一下两个这样的图匹配算法。

一个早期著名的子图同构算法由Ullmann开发【226】。在1976年的论文里，Ullmann将确定一个图G_a = (V_a, E_a)是否子图同构于另一个图G_b = (V_b,E_b) 的问题描述为找出一个布尔|V_a| × |V_b|矩阵Mꞌ，使得

C = Mꞌ (MꞌB)^T

∀i, j, 1 ≤ i ≤ |V_a|, 1 ≤ j ≤ |V_b|: (a_ij= 1) ⇒ (c_ij = 1)

成立，其中A与B分别是G_a与G_b的相邻矩阵。在Mꞌ这样的实例里，每行只包含一个1，而每列最多包含一个1。通过初始化每个单元mꞌ_ij为1，然后裁剪掉1直到找到一个解答来蛮力查找Mꞌ。为了减少查找空间，Ullmann开发了一个过程在开始查找前消除某些1。不过，该算法的最坏情况时间复杂度是O(n!n²)（根据【57】），并且使用相邻矩阵排斥了对可能出现在程序表示中多边界图的处理。

最近，Cordella等【57】提出了一个称为VF2的算法，它已经被用在几个基于DAG及图覆盖的指令选择器。特别的，它已经用于辅助指令集提取（instruction set extraction，ISE；参考【10，50，75】为例）。大致上，通过一个迭代的方式把一个新对加入集合，VF2算法递归地构造“(n,m)对”的一个映射集，其中n ∈ G_a而m ∈ G_b。该算法的核心是一个规则，它禁止添加阻止形成从G_a到G_b一个有效子图同构映射的对。在最坏情形下，该算法具有O(n!n)时间复杂度，但报告表示它已经被成功地应用于包含超过一千个节点的图，因为在最好的情形下，它具有多项式时间复杂度。另外，VF2算法可以处理多边界图（multi-edge graphs）。

在本调查进行中找到的、别的关于子图同构的论文包括：Guo等【119】，Krissinel与Henrick【152】，Sorlin与Solnon【213】（为查找子图同构展示了一个全局限制），Gallagher【102】，Fan等【82】，Fan等【83】，及Hino等【129】。

5.2.         第一批方法

在1994年，Liem等【165】在一篇被大量引用的论文里展示了一个在CDFG（控制及数据流图）上执行模式匹配与选择的做法。实现在一个称为CodeSyn的代码生成系统里——它又是一个称为FlexWare的嵌入式开发环境的一部分——这是第一个已知的技术，执行全局指令选择，同时处理数据流、控制流模式以及控制-数据流混合模式。虽然论文的做法局限于树模式，Liem等宣称它可以容易地扩展到DAG模式。他们的匹配算法在最坏情形下使用O(n²)时间，类似于Weingart的树模式匹配程序（参考3.1节），模式构成了单个类似树的结构。从该结构的根节点出发，匹配程序比较CDFG中的当前节点，在分支处深入。模式以这样一种方式排列，如果在该结构中更高处的匹配失败，可以删除整棵子树，因此减少了匹配时间。选择通过动态规划来完成。不过，Liem等没有提供一个方法来自动地排序模式以构建树，模式是否可以扩展到多个无关的图还存在疑问。

同一年，Van Praet等【227，228】开发了另一个方法，它实现在CHESS中，一个作为欧洲项目部分的面向DSP的编译器。在这个做法里，模式被自动从一个以nML编写的处理器描述导出——nML是一个由Fauth等构想的一个领域特定语言【85】——它指定了一幅由两部分构成，代表了目标处理器数据路径的图。在一个输入CDFG的代码生成过程里，处理器描述中的单元被分为包。然后这些包被转换为对应的模式（它可以是任意图形），接着匹配与选择模式。如果能产生一个更好的结果，模式允许重叠。论文没有讨论匹配过程，但声明使用了一个分支界定算法（branch-and-bound algorithm）完成选择。这个算法也假定所有的模式具有非负、不变的开销，这允许受处理的图被分解为更小、更简单，可以被单独覆盖的实例。不过，这阻止了对可以并行执行机器指令的利用，因为这样指令的选择不需要承担额外的开销。另外，不清楚在他们的方法中复杂处理器是否可以被正确地构建。

5.3.         单边及双边覆盖技术

解决模式选择问题的另一个方式是把它转换为一个等价的单边或双边覆盖问题。虽然基于双边覆盖的技术先出现，我们将先讨论单边覆盖，因为双边覆盖是单边覆盖的一个扩展。

5.3.1.   单边覆盖

Clark等【51】发表了一篇论文描述了用于非循环计算加速器（acycliccomputation accelerators）的代码生成方法。一个程序的部分可以由定制的加速器实现并执行，因此得到性能提升，在这个层面上，这样的加速器是可编程的。算法首先在输入的DAG上使用一个修改的Ullmann算法修剪不是子图同构的子图，枚举所有可能的子图（即模式）。一旦枚举了所有的模式，模式选择任务就被阐述为一个单边覆盖问题。这个问题包含了一个布尔矩阵M，其中列代表模式实例，行代表被覆盖的图形节点。因此，如果m_ij = 1，那节点i为模式实例j覆盖。这也显示在了图5.2里。因此，目标是选择列，使得每个节点以最小的代价被至少一个模式覆盖（该算法阻止重叠，Clark等辩论这减少了生成代码的功耗）。换而言之，如果N是输入图中的节点集合，P是模式实例的集合，那么

必须成立，同时最小化选中模式的总开销。作者在论文中（即【58,113】）提到他们考虑后认为，单边覆盖是解决这些问题已有、高效的启发式，他们的实验显示该算法显示出了线性的运行时间复杂度。这个方法后来被Hormati等【132】扩展，以减少加速器设计的互联与数据中枢的延迟。

图5.2：单边覆盖的例子。矩阵中以星号标记的1代表潜在、但没选中的覆盖，没有标记的1表示最优、选中的覆盖。假定所有的模式都有相同的单位开销。

单边覆盖也被Martin等【168】使用，但不像Clark等，他们把这个问题阐述为一个约束编程模型（CP）。然后，合并了指令调度，寻找这个CP模型的最优解决。这个做法也被Floch等【91】扩展来适应VLIW架构。

5.3.2.   双边覆盖

单边覆盖问题的矩阵可以重写为一个包含非互补析取的合取（conjunctions of uncomplemented disjunctions）的布尔公式。我们将每个析取记为一个子句（clause）。作为一个例子，图5.2（b）中的布尔矩阵可以重写为

f = (p₁ + p₂)(p₂+ p₃)(p₃ + p₄)(p₄ + p₅)p₆

因此目标是以最小开销满足f。不过，单边覆盖的问题是，它不能捕捉所有指令选择所必须的约束。大多数模式假定输入具有某个类型或位于一个特定的数据位置。在语法里，这通过非终结符来表示。使用相同的例子，让我们假设节点n₁可以被多个单节点模式p₁，pꞌ₁，及pꞌꞌ₁覆盖。让我们进一步假设模式p₃，如果选中，要求节点n₁必须被模式p₁覆盖，且仅为该模式覆盖。这样的约束，对指令选择来说是常见的，不能被表示为一个单边覆盖问题的部分。这个缺点通过双边覆盖来解决。不像单边覆盖，双边覆盖允许析取包含非互补及互补的字面（即 )。现在我们刚讨论的约束可以被表达为  + p₁，即如果我们选择p₃，那么我们必须也选择p₁，以使该子句为真。因此这样的子句被称为暗示子句（implication clauses），因为它等同于p₃ ⇒ p₁。

通过使用双边覆盖解决集成电路合成（VLSI synthesis）的DAG覆盖，Rudell【197】[1]引领了双边覆盖的应用。它也被Servít与Yi【206】应用来解决或多或少类似的技术变换（technology mapping）问题。

这个做法后来被Liao等【163，164】修改来处理指令选择。在他们分别发表在1995与1998年的论文里，Liao等描述了目标是一个寄存器的机器并优化代码大小的方法。为了控制复杂度，首先通过忽略数据传输及寄存器溅出开销来解决模式选择问题。在选择了复杂模式后，被覆盖节点缩合为单个节点，构建第二个双边覆盖问题以最小化数据传输的开销。虽然这两个问题可以被同时解决，Liao等选择不这样做，因为需要的子句数目会变得极大。

最近，Cong等【53】也把双边覆盖应用于指令选择，作为可配置处理器架构应用程序特定指令生成的一部分。不过，作者仅利用了之前的研究，而没有贡献将进一步推进指令选择的新知识。

虽然上面讨论的做法将自身局限于DAG，模式选择的双边覆盖思想可以扩展到任意图形模式。这，连同存在许多精确及近似解决双边覆盖问题的研究这个事实，使得它成为未来指令选择研究中一个有前途的候选。

1.2.         基于PBQP的做法

在2003年，Eckstein等【73】开发了第一个直接在SSA图上工作的技术。SSA代表静态、单赋值（static, single assignment），是一个程序表示形式，其中每个变量或临时变量仅定义一次。效果就是每个变量的生命周期是连续的，这简化了许多优化过程。因此，基于SSA的IR为许多现代编译器所使用，包括LLVM与gcc。关于SSA的更多信息，建议读者参考编译器教材【8】或【56】。

Eckstein等认识到在专用的DSP上执行定点算术运算的情形下，将指令选择限定在基本块会导致次优的代码。例如，在图5.3（a）中，我们看到一小段定点值乘法的代码。对于定点乘法，一个公共的乘法特性是，结果向左移一位。因此，为了有效地利用这样的乘法单元，在行4上的变量s中的结果在循环里必须维持左偏差，仅在函数返回前移回正常的模式。这意味着s的值在函数的不同点必须是不同的形式。不过，在限制在基本块的指令选择器中，这样的信息很难传播，因为s的定义与使用发生在不同的树中（参考图5.3的（b））。

[1]基于来自【53,163,164】的第二手资料。

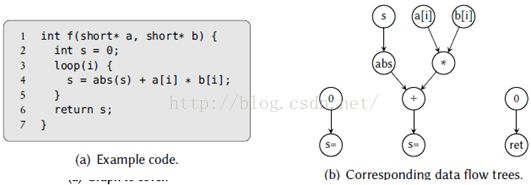
图5.3：一个将使全局指令选择受益的例子（来自【73】）

相比之下，全局指令选择器能够与模式选择合作做出这些决定。首先，输入程序被重写为SSA形式，从中导出对应的SSA图。图5.4显示当前这个例子的这些数据结构。因为SSA变量仅可以在一个点上定义，使用ɸ函数来定义循环变量以绕开这个限制。另外，因为SSA图不能包含控制流信息，代码流出必须把输入程序作为额外输入，以推断如何安排机器指令。

假定模式被表示为一个线性语法（参考20页的描述）。所有正常的语法可以容易地重写为线性形式的语法。对于SSA图中的每个节点n_i，我们定义一个布尔向量x_i，长度等于匹配该节点的基本规则数。在这里，匹配仅意味着一个基本规则的操作符匹配这个节点。它不一定意味着对子节点存在一个有效的规则推理，使得父规则可以被实际选中。相反，这将被我们很快会讨论的链开销来接管。因此我们可以认为这稍微把匹配问题放松了一点，然后将有效的匹配推论为部分模式选择问题。进一步假定适用的基本规则的权重开销由等长的另一个向量c_i给出。权重通常是估计的，节点操作的相对执行频率。给予循环中的低开销指令更高优先级是需要的，因为它们对性能有更大的影响。使用这些定义，SSA图被变换为一个分区布尔二次问题（partitioned Boolean quadratic problem，PBQP；也是由Scholz与Eckstein描述【203】），这被定义为查找对x_i的赋值，使得

是最小的，其中n是SSA图中的节点数。解也被限制在那些在每个向量x_i（即x_i⋅1^T = 1）只有一个1的解。PBQP是二次分派问题（the quadratic assignmentproblem，QAP）的一个扩展，它是一个基本的组合优化问题。QAP与PBQP都显然是NP完全问题，Eckstein等开发了自己的启发式解答，这也在论文中描述了。

图5.4：图5.3的SSA形式（来自【73】）

显然，这个目标函数包含两部分：积累的链开销（这是第一个项），及积累的基本开销（这是第二个项）。基本开销是显而易见的，将不再进一步讨论。链开销是通过链规则从一个基本规则迁移到另一个基本规则的开销。这个开销由开销矩阵C_ij给出，它代表在SSA图中从节点j迁移到节点i的链开销。假定SSA图的边必须排序，节点j是节点i的第m个子节点。那么，这个矩阵的元素c_kl给出了使用规则l的非终结符作为规则k的第m个参数所必须的链规则的最小开销。如果非终结符是相同的，这个开销是0。如果不存在这样的链规则，开销值则设为∞，禁止这样规则组合的选择。通过为所有的链规则计算传递闭包来计算链开销，可以使用Floyd-Warshall算法【92】（虽然也存在其他算法）。后来Schäfer与Scholz【201】发现一个如何最优地应用这些链规则的方法。

精明的读者可能注意到这个规划假定SSA图不包含重边（multi-edges）。这阻止了比如：y = x + x的表达式直接建模。幸运的是，重边可以通过引入新的临时变量，并通过值拷贝连接它们来删除。即

Eckstein等在选定的问题上测试了他们的实现。结果显示，对比传统的树模式匹配程序，这个做法提升了代码质量40–60%（对于一个问题最多到90%）。PBQP求解器对几乎所有测试用例产生了最优结果。不过，这个方法局限于树模式，这阻碍了对许多复杂机器指令的利用。

这个局限后来被Ebner等【72】去除。首先语法被扩展为对给定的模式允许规则元组（tuples of rules），即一条开销为2的除法-求模指令可以被表示为下面的复杂模式：

⟨lo → div(x : reg₁,y : reg₂), hi → mod(x, y)⟩

       [2]{emit divmod r(reg₁),r(reg₂)}

x和y是允许div及mod操作的规则表示共享相同输入的索引。自此之后，从属于复杂模式的基本规则被称为代理规则（proxy rules）。那么PBQP问题被修改为包容复杂模式的选择。本质上，这必须引入新的表示一个复杂模式是否被使用的变量，连同强制一个选中作为复杂模式部分的所有代理规则也被选中的限制。我们还需要防止选中导致循环依赖的复杂模式的限制。让我们进入细节。

首先，从匹配节点i的复杂模式推导的代理规则扩展节点i的向量x_i。如果来自不同复杂模式的两个或更多代理规则是相同的， 向量的长度仍然仅增长1个元素。

其次，为独立节点的每个组合创建一个复杂模式实例，其中匹配的代理规可以合并为该复杂规则。每个实例产生了一个决策向量x_l，表示该实例l是否被选中。让我们把所有的x_i向量集合进一个变量类别X₁，并把所有的决策向量x_l集合进另一个变量类别X₂。X₁与X₂之间的联系是这样的，如果x_l是选中的集合，其中i是作为l部分的一个代理规则匹配的节点，那么x_i中所有对应的代理规则必须也是选中的集合。这需要额外的开销矩阵 ，其中对应下者之一元素的值设置为0：

·        x_l将被设为没有选中，或者

·        x_i将被设置为不与复杂模式实例l关联的一个基本规则或代理规则。

其他所有值设为∞。不过，如果所有代理规则的开销都是0，那么允许这样的解答，其中一个复杂模式l的所有代理规则被选中，但该复杂模式本身没有。Ebner等通过对所有代理模式设置一个高的开销M，并把所有复杂模式的开销修改为cost(l) – |l|M，其中|l|是l中代理规则数，来解决这个问题。这抵消了选中的代理模式的人为开销，将选中代理规则与复杂模式的总体开销降低到cost(l)。

最后，如果两个复杂模式实例u与v重叠或选中会导致循环数据依赖，我们需要一个防止它们被同时选中的开销矩阵 。这可以通过将对应违反这两个条件情形的 元素的值设置为∞，其他设置为0来保证。

因此，如果我们将原来PBQP问题中的C_ij开销矩阵重命名为 ，新的目标函数变成

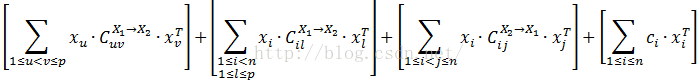
其中p是复杂模式实例的数目。以ARMv5作为目标处理器与LLVM 2.1比较，对于一组选定的问题，以执行时间衡量，PBQP解决方案平均改善了13%。在编译时间上总体的影响可以忽略不计。

另一个将第一个PBQP实现扩展为一般图形模式的技术由Buchwald与Zwinkau【35】展示。Buchwald与Zwinkau将指令选择作为一个形式化的图形转换问题来着手，其中许多之前的工作业已存在，机器指令被表示为重写规则，而不是语法规则。除了扩展模式的支持，形式化的基础可以验证得到的指令选择器可以处理所有可接受的输入。如果验证失败，可以自动推导必须的，缺失的重写规则。在为SSA图找到所有适用的重写规则（这相当于匹配模式）后[1]，形成一个对应的PBQP实例，并如前求解。Buchwald与Zwinkau还发现并处理了这些情景，因为信息的传播不足够，Eckstein等的启发式求解程序的实现可能不能找到一个解答。不过在论文里，Buchwald与Zwinkau提到在重叠模式数量增加时，他们当前实现的伸缩性不好。

对比其他技术，依赖于PBQP的做法看起来在机器指令支持、代码质量及运行时方面非常有希望。不过，因为基于PBQP的指令选择器是相当新的发明，引用数及在工业级编译器中的应用仍十分少。另外，尚不清楚它们是否能处理所有类型的机器指令，特别是那些有特别限制的DSP指令。

5.5.         其他基于图的做法

Yu与Hu【245】展示了一个技术，对模式选择，它依赖一个基于手段目的分析（means-end analysis）的递归、启发式的搜索方法[2]。据称，这个做法强大到足以将整个函数作为输入，但作者没有进入细节。这里提这篇论文只是为了完整。

一个非传统的技术由Visser提出【229】，他对代码生成应用了模拟退火的理论【147】。虽然有趣，指令选择问题不幸被简化为IR节点与选中机器指令间的一一映射，因而在实践中没有什么用。

5.6.         总结

在本章，我们考虑了若干依赖图覆盖的指令选择技术。对比工作在树或DAG上的代码生成器，基于图形覆盖的指令选择器是最强大的，因为程序输入及机器指令可以是任意图形。这使包含整个函数，包括控制流，匹配并选择不能被树或DAG建模的更复杂机器指令的全局指令选择器成为可能。

不过，因为子图同构是一个NP完全问题，最优图覆盖要求两个NP完全问题，而不“只是” DAG覆盖的一个。因为这恶化了本已巨大的挑战，最有可能，我们将只在可以承受用非常长的编译时间换取最优或近似最优代码质量的编译器中看到这样的做法（即在有极端高的性能、代码大小或功耗要求的嵌入式系统里）。

[1] 实际上，通过将ɸ节点分裂为两个节点打破回环，SSA图首先被转换到一个DAG。

[2] 类似的思想之前由Newell与Ernst【178】应用于基于树覆盖的指令选择（参考第7页）。