JZOJ.3431【GDOI2014模拟】网格 解题报告

网格

题目描述

某城市的街道呈网格状，左下角坐标为A(0, 0)，右上角坐标为B(n, m)，其中n >= m。现在从A(0, 0)点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点(x, y)都要满足x >= y，请问在这些前提下，到达B(n, m)有多少种走法。

样例输入

6 3

5 3

样例输出

132

28

数据范围

50%的数据中，n = m，在另外的50%数据中，有30%的数据：1 <= m < n <= 100
100%的数据中，1 <= m <= n <= 5 000

题解

关于这种不能穿过某条直线的网格行走问题，先讲一下怎么做。
我们知道，答案就等于走到点（n,m）的所有路径数量减去穿过这条直线的路径数量。
我们还知道由点（0,0）走到点（n,m）的路径数为 Cn(m)n+m 。

所以我们现在只需求得穿过这条直线的路径数量就可以知道答案了。
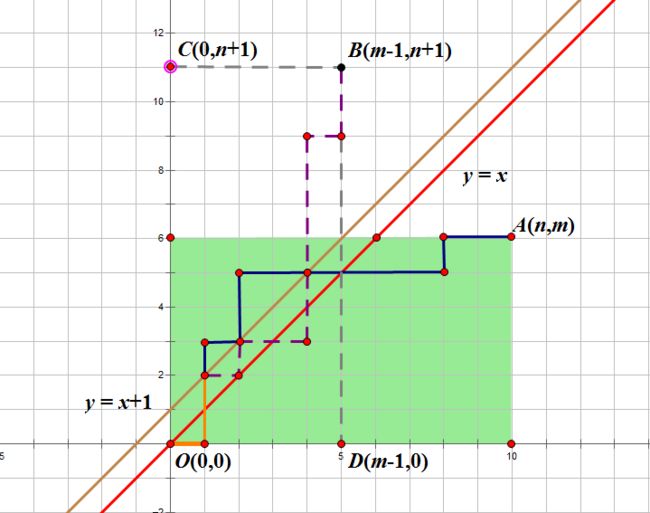
对于一个如下的网格，有这样的一条违法路径穿过了y=x这条直线。

易知，不能穿过y=x这条直线就等于不能碰到y=x+1，所以我们找到y=x+1这条直线（图中为棕色直线），并将原路径沿这条直线对称过去（除了最下面的一段，图中为橙色），可以得到下图

像这样，路径中点A(n,m)会对称到点B(m-1,n+1)，并且从原点走到对称点B(m-1,n+1)的一条路径都可以对称回来，并对应着一条从原点走到终点A(n,m)且穿过y=x直线的路径。

所以穿过直线y=x的路径数就对于从原点走到对称点的路径数。
走到对称点B(m-1,n+1)的路径数 SB = Cm−1n+1+m−1 = Cm−1n+m
走到原终点A(n,m)的路径数 SA = Cmn+m
则

Ans = SA - SB

= Cmn+m - Cm−1n+m

= (n+m)!m!∗n! − (n+m)!(m−1)!∗(n+1)!

= (n+m)!∗(n+1)m!∗(n+1)! − (n+m)!∗mm!∗(n+1)!

= (n+m)!∗(n+1−m)m!∗(n+1)!
再约一下分，得

Ans = (n+2)∗(n+3)∗(n+4)∗......∗(n+m)∗(n+1−m)m!

分数线上面的部分我们可以用高精度乘法将积算出来。
那份木怎么办呢？
我们看到数据范围，惊奇的发现m<=5 000，于是可以打一个单精度除法除m次。
因为直接打会超时，所以打高精度时要压位，否则会超时。

Code(Pascal)

const
    mo=100000000000000;
var
    lj,dt:array[0..30000] of int64;
    n,m,j,i,l:longint;
    k,o:int64;
procedure cs(o:int64);
    var
        i,j,l:longint;
        hhh:int64;
    begin
        hhh:=0;
        for i:=1 to lj[0] do
        begin
            dt[i]:=lj[i]*o+hhh;
            hhh:=dt[i] div mo;
            dt[i]:=dt[i] mod mo;
        end;
        dt[0]:=lj[0];
        while hhh>0 do
        begin
            inc(dt[0]);
            dt[dt[0]]:=hhh mod mo;
            hhh:=hhh div mo;
        end;
        for i:=0 to dt[0] do
        lj[i]:=dt[i];
    end;
procedure cd(o:int64);
    var
        i,j,l:longint;
        hhh:int64;
    begin
        for i:=lj[0] downto 1 do
        begin
            dt[i]:=(lj[i]+hhh) div o;
            hhh:=(lj[i]-dt[i]*o+hhh)*mo;
        end;
        dt[0]:=lj[0];
        while (dt[dt[0]]=0) and (dt[0]>0) do
        dec(dt[0]);
        for i:=lj[0] downto dt[0] do
        lj[i]:=0;
        for i:=0 to dt[0] do
        lj[i]:=dt[i];
    end;
begin
    readln(n,m);
    lj[0]:=1;
    lj[1]:=1;
    for i:=n+2 to n+m do
    cs(i);
    cs(n+1-m);
    for i:=1 to m do
    cd(i);
    write(lj[lj[0]]);
    for i:=lj[0]-1 downto 1 do
    begin
        k:=lj[i];
        o:=0;
        while k>0 do
        begin
            inc(o);
            k:=k div 10;
        end;
        for l:=1 to 14-o do
        write(0);
        write(lj[i]);
    end;
end.