顺时针打印矩阵
牛客网AC地址:http://www.nowcoder.com/books/coding-interviews/9b4c81a02cd34f76be2659fa0d54342a?rp=1
《剑指offer》面试题20:顺时针打印矩阵
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。例如:如果输入如下矩阵:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
则依次打印出数字1、2、3、4、8、12、16、15、14、13、9、5、6、7、11、10。
思路:
分析这个问题,我们可以借助图形来帮助我们思考。
由于是从外圈到内圈的顺序依次打印,我们可以把矩阵想象成若干个圈,如下图所示。
我们可以用一个循环来打印矩阵。每一次打印矩阵中的一个圈。
但是循环什么时候结束呢?
假设这个矩阵的行数是rows,列数是cols。打印第一圈的左上角的坐标是(0,0),第二圈的左上角的坐标是(1,1),依此类推。——这里,左上角的坐标中,行标和列标总是相同 的,于是可以在矩阵中选取左上角为(start,start)的一圈作为我们分析的目标。
再接着分析循环到什么时候?
画几个矩阵试试看,我们会发现让循环继续的条件是cols>startX×2并且rows>startY×2。所以用如下循环来打印矩阵:
void PrintMatrixClockwisely(int** numbers, int cols, int rows) {
if (numbers == NULL || cols <= 0 || rows <= 0)
return;
int start = 0;
while(cols > start*2 && rows > start*2) {
PrintMatrixInCircle(numbers, cols, rows, start);
++start;
}
}
下面具体分析如何打印一圈的功能——如何实现PrintMatrixInCircle。
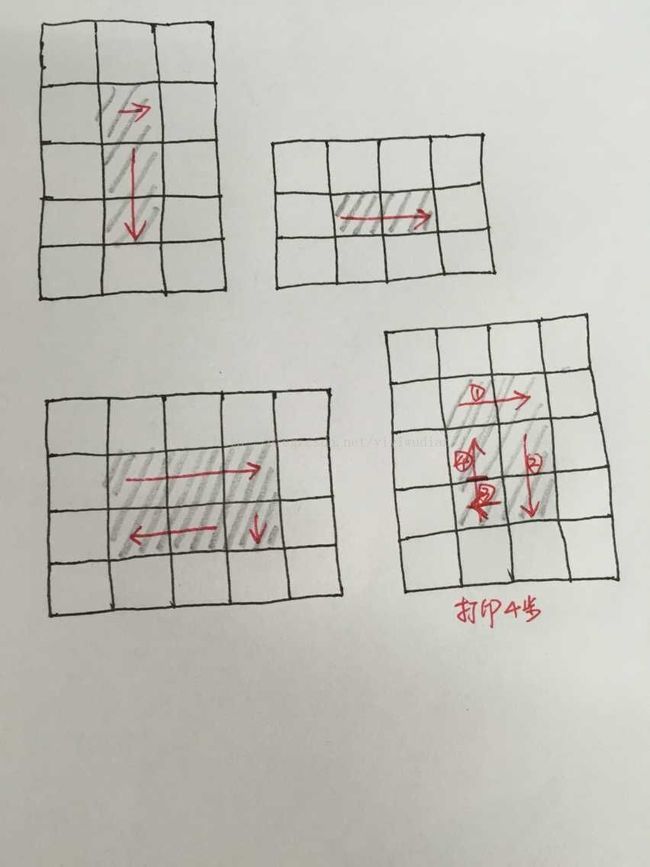
如第一个图所示,我们可以把打印一圈分为四步:
第一步从左到右打印一行,
第二步从上到下打印一列,
第三步从右到左打印一行,
第四步从下到上打印一列。
每一步我们根据根据起始坐标和终止坐标用一个循环就能打印出一行或者一列。
这里值得注意的是,最后一圈有可能退化成只有一行、只有一列,甚至只有一个数字,因此打印这一圈就不需要四步。下图是几个退化的例子。
因此,我们需要分析打印每一步时的前提条件。
第一步总是需要的,因为打印一圈至少有一步。
如果只有一行,那就不用打印第二步了,由此第二步的前提条件是终止行号大于起始行号。
需要第三步打印的前提条件是,圈内至少有两行两列,即除了要求终止行号大于起始行号外,还要求终止列号大于起始列号。
需要打印第四步的前提条件是至少有三行两列,因此要求终止行号比起始行号至少大2,同时终止列号大于起始列号。
通过上述分析,可写出代码:
void PrintMatrixInCircle(int** numbers, int cols, int rows, int start) {
int endX = cols - 1 - start;
int endY = rows - 1 - start;
// 从左到右打印一行
for (int i = start; i <= endX; ++i) {
int number = numbers[start][i];
printNumber(number);
}
// 从上到下打印一列
if (start < endY) {
for (int i = start + 1; i <= endY; ++i) {
int number = numbers[i][endX];
printNumber(number);
}
}
// 从右到左打印一行
if (start < endX && start < endY) {
for (int i = endX - 1; i >= start; --i) {
int number = numbers[endY][i];
printNumber(number);
}
}
// 从下到上打印一列
if (start < endX && start < endY - 1) {
for (int i = endY - 1; i >= start + 1; --i) {
int number = numbers[i][start];
printNumber(number);
}
}
}
这道题目没有涉及复杂的数据结构,只是需要仔细分析执行过程。上述过程基本来自《剑指offer》,下面是自己的AC代码:
需要注意的一点是,最后打印的前提条件,需要避免重复打印角落的number。
public class Solution {
public ArrayList<Integer> printMatrix(int[][] matrix) {
ArrayList<Integer> matrixList = new ArrayList<Integer>();
if (matrix == null || matrix.length == 0) {
return null;
}
int row = matrix.length; // 行
int col = matrix[0].length; // 列
int start = 0;
while (col > start * 2 && row > start * 2) { // 从外圈到内圈
int endX = col - start - 1;
int endY = row - start - 1;
for (int i = start; i <= endX; i++) { // 从左到右
matrixList.add(matrix[start][i]);
}
if (start < endY) {
for (int i = start + 1; i <= endY; i++) { // 从下到上
matrixList.add(matrix[i][endX]);
}
}
if (start < endX && start < endY) {
for (int i = endX - 1; i >= start; i--) { // 从右到左
matrixList.add(matrix[endY][i]);
}
}
if (start < endX && start < endY - 1) {
for (int i = endY - 1; i >= start + 1; i--) { // 从下到上
matrixList.add(matrix[i][start]);
}
}
start++;
}
for (int i = 0; i < matrixList.size(); i++) {
System.out.print(matrixList.get(i) + " ");
}
return matrixList;
}
// 用一维数组建立行尾row,列为col的矩阵(二维数组)
public int[][] createMatrix(int[] arr, int col, int row) {
int[][] matrix = new int[row][col];
int i = 0;
for (int j = 0; j < row; j++) { // 逐行写入
for (int k = 0; k < col; k++) {
if (matrix[j][k] == 0) {
matrix[j][k] = arr[i++];
}
}
}
return matrix;
}
// 逐行打印矩阵
public void printMatrixOriginal(int[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
上述代码除所需要的printMatrix方法外,还提供了矩阵的逐行打印,用一维数组建立二维数组,另需要注意获取行号和列号。提交代码的时候,需要把打印matrixList的地方去掉,否则运行不通过。
int row = matrix.length; // 行 int col = matrix[0].length; // 列
最后是测试代码:
public class Main {
public static void main(String[] args) {
Solution test = new Solution();
int[] arr = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
int[][] matrix = test.createMatrix(arr, 4, 4);
System.out.println("原来创建的矩阵:");
test.printMatrixOriginal(matrix);
System.out.println("顺时针打印矩阵:");
test.printMatrix(matrix);
}
}
运行结果是: