LeetCode总结,回溯法小结
一,回溯法思想
回溯法概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
基本思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
解题一般步骤
(1)针对所给问题,确定问题的解空间:首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
二,回溯法典型
1,八皇后问题
转化规则:其实八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。令一个一维数组a[n]保存所得解,其中a[i] 表示把第i个皇后放在第i行的列数(注意i的值都是从0开始计算的),下面就八皇后问题的约束条件。
(1)因为所有的皇后都不能放在同一列,因此任意两个a[0].....a[7]的值不能存在相同的两个值。
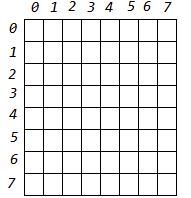
(2)所有的皇后都不能在对角线上,那么该如何检测两个皇后是否在同一个对角线上?我们将棋盘的方格成一个二维数组,如下:
穷举法:
#include <iostream>
#include <algorithm>
#include <iterator>
#include <vector>
using namespace std;
//位置冲突算法
bool isMeet(int a[], int n)//a[]位置数组,n皇后个数
{
for (int i = 2; i <= n; ++i)//i:位置
for (int j = 1; j < i; ++j)//j:位置
if ((a[i] == a[j]) || (abs(a[i] - a[j]) == i - j))//1:在一行;2:在对角线上
return false; //冲突
return true;//不冲突
}
//八皇后:枚举算法
//主函数
int main()
{
int a[9] = { 0 }; //用于记录皇后位置:(第0行0列我们不用)。如:a[3] = 4;表示第3列第4行位置有皇后
int count = 0; //用于计数
for (a[1] = 1; a[1] <= 8; ++a[1])
for (a[2] = 1; a[2] <= 8; ++a[2])
for (a[3] = 1; a[3] <= 8; ++a[3])
for (a[4] = 1; a[4] <= 8; ++a[4])
for (a[5] = 1; a[5] <= 8; ++a[5])
for (a[6] = 1; a[6] <= 8; ++a[6])
for (a[7] = 1; a[7] <= 8; ++a[7])
for (a[8] = 1; a[8] <= 8; ++a[8])
{
if (!isMeet(a, 8))//如果冲突,则继续枚举
continue;
else
++count;
}
cout << count << endl;
system("pause");
return 0;
}
回溯法递归版:
见leecode,<LeetCode OJ> 52. N-Queens II
#include <iostream>
#include <algorithm>
#include <iterator>
#include <vector>
using namespace std;
int a[9] = { 0 };
int n = 8, cnt = 0;
//位置冲突算法
bool isConflict(int a[], int n)//a[]位置数组,n皇后个数
{
int i = 0, j = 0;
for (i = 2; i <= n; ++i)//i:位置
for (j = 1; j <= i - 1; ++j)//j:位置
if ((a[i] == a[j]) || (abs(a[i] - a[j]) == i - j))//1:在一行;2:在对角线上
return false; //冲突
return true;//不冲突
}
//八皇后问题:回溯算法(递归版)
void Queens8(int k) //参数k:递归摆放第k个皇后
{
int i = 0;
if (k > n) //k>n:即k>8表示最后一个皇后摆放完毕
{
printf("第%d种情况:", ++cnt);
for (i = 1; i <= n; ++i)
printf("%d ", a[i]);//打印情况
printf("\n");
}
else //8个皇后未全部摆放完毕
{
for (i = 1; i <= n; ++i)//摆放第k个皇后时(转下一行)
{ //依次从列顶端开始搜索,一直到列底端,直到找到合适位置,如果未找到,自动返回上层递归(回溯)
a[k] = i;
if (isConflict(a, k))
Queens8(k + 1);//不冲突,递归摆放下一个皇后
}
}
return;
}
//主函数
int main()
{
Queens8(1);//参数1:表示摆放第1个皇后
system("pause");
return 0;
}
三,典型例题
在leetcode中,那些要求列举所有情况,或者说所有情况都要探讨一下的的例题,一般都可以考虑回溯法。
当遇到一个可以用到回溯法的时候需要按照如下步骤进行:
1. 确定问题的一个解空间树, 这个解空间树至少包含一个你需要的那个解, 否则这个树就完全没有意义了
2. 组织好这棵树, 弄明白这棵树的每一个节点代表什么, 每一个分支代表什么
3. 从这棵树的根节点不断的向下深搜, 当遇到不合适的节点的时候直接跳过以这个节点为根的子树
4. 当搜索到了叶子节点的时候就回溯
5. 不断的重复这个3, 4步骤
附加: 根据具体的问题可以定义限界条件, 最优值条件, 根据这两个条件可以剪枝了
以下是在leetcode中收集的典型例子。
<LeetCode OJ> 39 / 40 / 216 Combination Sum(I / II / III)
<LeetCode OJ> 78 / 90 Subsets (I / II)
<LeetCode OJ> 46. / 47. Permutations (I / II)
<LeetCode OJ> 22. Generate Parentheses
<LeetCode OJ> 17. Letter Combinations of a Phone Number
注:本博文为EbowTang原创,后续可能继续更新本文。如果转载,请务必复制本条信息!
原文地址:http://blog.csdn.net/ebowtang/article/details/38145433
原作者博客:http://blog.csdn.net/ebowtang
参考资源:
【1】写的很不错,很清楚,http://www.2cto.com/kf/201405/302318.html