KMP算法<坑已挖>

按理说KMP算法我早就会了应该早点写这个blog的QAQ

古人告诉我，凡是你5分钟讲不明白的算法，那就代表你自己也不明白这个算法。
KMP算法，其实自己也是YY过的，然而因为自己并没有发现字符串匹配的规律，所以吧，
还是不要立这个flag比较好。
我看着各种早就会后缀自动机的神犇留下了悔恨的泪水QAQ

字符串匹配：
哈希？
嗯……维护一个前缀哈希值的确是可取的。
KMP算法是基于暴力匹配太差而研究出来的。
简单想一想实际上就是：
1.S串到i，C串到j。
2.i + 1与j + 1处失配。
暴力：S串到i + 1 - j，C串到0。
KMP:找出它们可利用的部分，并直接向后移动C串，看看是否存在 k< j && S[(i - k + 1) ->(i + 1)] == C[1…k]
这就是KMP的思想，问题在于，可利用的部分是什么？怎么找出它们可利用的部分？
嗯……实际上，这次匹配跟S串无关，而是跟C串匹配到哪里有关，实际上从头到尾都是C串的匹配位数在动。
这样我们考虑：
可利用的部分显然就是：
C串后缀与C串的前缀的最大匹配长度。
比如说abc，那么C串就算是匹配到第3位c失配掉，它也只能从头开始。
但是abababc就不一样，它如果匹配到第6位失配掉了，我们可以考虑这样做：
以下为模拟过程：

S串：…abababx
C串：abababc
失败。
S串：…XXababx(大写X代表已经不可能是匹配的字符)
C串：abababc
嗯……我们此时已经至少知道，C串必须向前移动两位，没错吧。
也就是说，之前C串匹配的长度为6，现在为4，它每次失配之后，再次能匹配的长度只有可利用的部分，也就是：
C串后缀与C串的前缀的最大匹配长度。

我们定义next[i]为C[1…i]的前缀与后缀的最大匹配长度，那么则有：
if(C[j + 1] != S[i])j = next[j];
因为假设下一位不和它匹配，那么它最大的匹配长度一定只有next[j]这么长的匹配长度。
所以我们仔细想一下，应该是可以暴力处理出每一个next[i]的，这样复杂度应该是 O(lenc2)
这样是不能接受的，所以我们考虑这样：
假设我现在计算出next[i - 1]，它的值为j。
那么如果c[i] == c[j + 1],next[i] = next[i - 1] + 1。
显然，C[1…i]的所有后缀都是因为加了一个新元素而进行了改变，我们考虑实际上……？
我们可以暴力扫一遍C[1…next[i - 1]]，但是显然是没有必要的，因为C[i]和C[j + 1]就算不相等，next[i]的答案一定也只出在next[j] ,next[next[j]],…的这里面。
证明：
显然，next[i - 1] + 1 >= next[i]
如果不处在next[j]里面，则：
因为next[i]表示最长的公共前后缀，我们把C[i]这个元素从next[i]中剔除，再最后加上1，则：
next[i]退掉一位等于什么？
也就是C[1…i - 1]中的使得C[next[k] + 1] == C[i]中最大的next[k]。
我们只需要证明它都在next[j]里面就好了。
考虑这样一个事实：
如果不在next[j]里面，比如是next[k]，且k不在next[j]所组成的集合中。
那么我们考虑，显然k前面的转移都是因为新加入的字符等于前缀的后一个字符转移的，所以我们会知道它肯定是处于next[j]的集合中的，并且比较大的next值肯定要先被检验到。

胡言乱语了一通
我们现在考虑KMP算法的流程：
1.求出每个的next数组，复杂度是O(n)的。
2.考虑匹配S串到i，C串到j + 1,此时失配掉了。
3.C串的匹配长度变为next[j]，看看能不能使得S[i] = C[j + 1]<即while(j && S[i] != c[j + 1])j = next[j];>
4.考虑匹配可不可以重叠，如果不可重叠记得在匹配后把j清零，不然直接等于next[j]就成了。

//模板poj3461
#include <cstdio>
#include <cstring>
#include <algorithm>
#define Rep(i,n) for(int i = 1;i <= n;i ++)
using namespace std;
#define M 1000010 
int nxt[M];
void Get(char *c)
{
    nxt[1] = 0;
    int j = 0,len = strlen(c + 1);
    for(int i = 2;i <= len;i ++)
    {
        while(j && c[i] != c[j + 1])j = nxt[j];
        if(c[i] == c[j + 1])j ++;
        nxt[i] = j;//最长公共前后缀长度 
    }
}
int KMP(char *c,char *s)
{
    int lenc = strlen(c + 1),len = strlen(s + 1),j = 0,cmt = 0;
    Rep(i,len)
    {
        while(j && s[i] != c[j + 1])j = nxt[j];
        if(s[i] == c[j + 1])j ++;
        if(j == lenc)cmt ++;
    }
    return cmt;
}
char c[M],s[M];
int main ()
{
    int T;
    scanf("%d",&T);
    while(T --)
    {
        scanf("%s%s",c + 1,s + 1);
        Get(c);
        printf("%d\n",KMP(c,s));
    }
    return 0;
}

一定会很快补充AC自动机和后缀数组什么的。
后缀数组看过一遍之后很快忘了，显然是自己信心不足，如果当时能够自己冲一下可能就会了呢。
Update On 2016-5-30-0:22

//未完待续？
//今天考得很差，第一题LCT+线段树被我生生看成树链剖分……
//错排问题一点不会
考虑AC自动机是个什么东西之前，我们还是先来看一下Trie树：

Trie树，你可以认为是一个树，它每个节点上都有字母。
我们用链表的方法来存储Trie树，根节点为0.

#define v ch[x][c]
void Ins(char *s){
    int len = strlen(s + 1),x = 0;
    Rep(i,len)
    {
        int c = s[i] - 'a';
        if(!v)v = ++ sz;
        x = v;
    }
    End[x] ++;
}

这个意思大概就是：
首先来到Trie的根，然后：
1.Trie之前有没有插入过与s[i]相同的节点//这里我们因为从根节点开始，所以就是看s[1]这个节点是否为根的子节点，假设没有，那么新建。
2.如果没有的话就一路新建下去了，我们还是让它有子节点吧。
3.有子节点，那么我们跑到对应的那个子节点，然后看一看这个节点有没有s[2]这个节点，如果有的话就跑到s[2]…
4.然后如果跑到一个地方没有了，而s串还没有到达结尾，那么剩余节点都新建。

然后我们可以在Trie树上dfs，这样什么都做不了

讲完Trie树之后，领会精神，发现我们可以把KMP的思想应用到Trie上。
多串匹配的方法：
考虑现在某个最长的串c已经匹配到了j，但是s[i] != c[j + 1]。
怎么办呢？如果是KMP算法的话，就自己回到c[next[j]]去看了，但是这不一定是最优的，因为有可能别的串的前缀和c串的后缀的最长匹配长度 > c串后缀与c串本身的前缀的最长匹配长度。
话有点绕，表达一下就是：
b[1…p] == c[j - p + 1…j]，c[1…next[j]] == c[j - next[j]…j]
然而p > next[j]
那就意味着，如果我们跳到串b的第p个位置上，一定比自己跳来跳去要优。
我们建立一个Fail指针，Fail指针的含义是：
指向所有串的最长前缀与后缀的匹配长度……的那个节点的那个指针。
我们考虑abcabc这一个串。
仅仅是一个串的话：

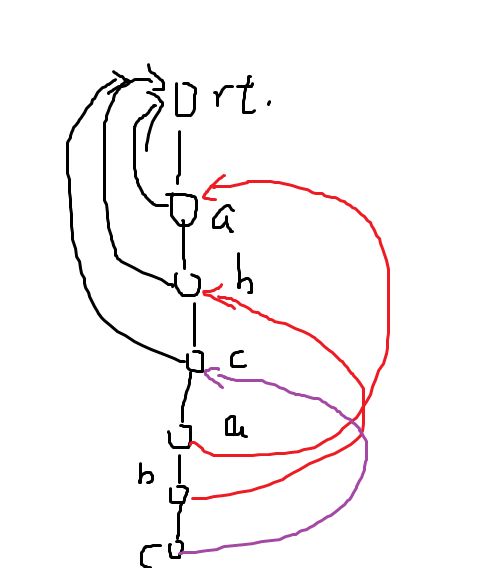
我们就只需要找到它自己一个串的即可。
这个其实就是KMP的next数组。
考虑next数组是怎么建立的：
看c[j + 1]与c[i]是否相等，如果不相等，那么j = next[j]，然后继续判断。最后next[i] = j.
我们多个串其实也无非如此。

我们考虑点x的Fail指针如何建立，就是看点x的父亲fa[x]的Fail指针指向哪里，如果Fail[fa[x]]指向了点y，那么看一下点y存不存在一个节点和x所对应的字符相同，如果不相同，那么继续走y的Fail指针……
如果走到最后一个都没有，那么直接指向root，表示这个后缀与所有串的最大匹配长度都是0.
我们只需要bfs一遍整个Trie树，就可以构建出Fail指针了。

#define v ch[x][c]
#define f ch[Fail[x]][c]
void Build()
{
    int h = 0,t = -1;
    Rep_0(c,26)if(v)q[++ t] = v;
    while(h <= t)
    {
        int x = q[h ++];
        Rep_0(c,26)
        {
            if(v)Fail[q[++ t] = v] = f;  
            else v = f;
        }
    }
}

注意这段代码并没有判断Fail[x]的儿子是否有c，那是因为我建立这些之前，首先把空节点的Fail指针都指向了Fail[x]的那些对应节点(即使那些对应节点是空的也无所谓)，所以也就意味着，如果它找不到这个对应节点，它的Fail指针也就为空了。
总之领会下精神也确实是对的。

然后发现我并没有直接学习AC自动机而是直接学的Trie图。
实际上上面讲的是Trie图。
上面的Build方法，在每个节点的所有后继中，都连了边。
比如之前的这个图，我们只需要在所有节点的后继节点都向接受这个字符之后能到达的那个最优状态连上边即可，无论这些节点是否存在。
上面这个图加了一笔之后意思就是这样：

a的后继c是不存在的，但是如果a接受到了c字符，那么实际上就直接跳到右侧那个c处即可。