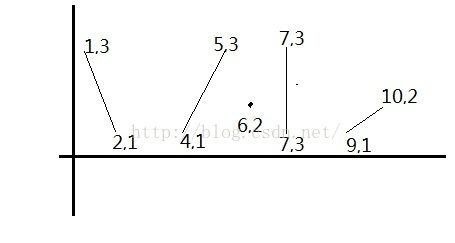
利用叉积判断点和线的关系

用叉积判断点在线的左侧还是右侧：

记住那句话，逆正顺负（因为参数的设置不同而不同）

9

3

-2

4

--------------------------------

Process exited with return value 0

Press any key to continue . . .

运行代码：

#include <iostream>  
#include <cstdio>  
#include <cstring>  
using namespace std;  
const int maxn=5e3+10;  
struct point {  
    int x,y;  
}; 
point p={6,2};
struct node{
    point p1,p2;
}edge[4];
int multi(point p0,point p1,point p2){  
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);  
}  
int m[4][4]={
1,3,2,1,
5,3,4,1,
7,3,7,1,
9,1,10,2  //特殊设置
};

int main(){
    for(int i=0;i<4;i++){
        edge[i].p1.x=m[i][0];
        edge[i].p1.y=m[i][1];
        edge[i].p2.x=m[i][2];
        edge[i].p2.y=m[i][3];
    }
    for(int i=0;i<4;i++)
    cout<<multi(edge[i].p1,edge[i].p2,p)<<endl;

    return 0;
}

当点在线段的上时，叉积是0而且点到两端点的而距离和等于线段的长度，如果大于就是在延长线上。当叉积是正数，逆时针方向，负数，顺时针方向。

这一切都和函数参数密切相关：

int multi(point p0,point p1,point p2){  
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);  
}
// ……
 cout<<multi(edge[i].p1,edge[i].p2,p)<<endl;

相关例题：

http://poj.org/problem?id=2318

代码参考：

http://blog.csdn.net/thearcticocean/article/details/48632391

有时需要我们求出线段相交的交点，曾经研究过： http://blog.csdn.net/thearcticocean/article/details/48765019