三维曲面总结:平面拟合、RANSAC、ICP算法
ACM算法分类:http://www.kuqin.com/algorithm/20080229/4071.html
(1):拟合一个平面:
空间平面方程的一般表达式为:
![]()
则有:
![]()
对于空间中n个点(n![]() 3):
3):
![]()
根据最小二乘法则用这n个点拟合上述平面方程,则要使下式的值最小:
(下面公式应为乘方,不是线性组合:)
空间方程的拟合为:
由上式解出:
![]()
即得到平面方程:
![]()
注意:这个方法是直接的计算方法,没办法解决数值计算遇到的病态矩阵问题.在公式转化代码之前必须对空间点坐标进行近似归一化!
(2):空间向量的旋转:
2-D绕原点旋转变换矩阵是:
[cosA sinA] [cosA -sinA][-sinA cosA] 或者 [sinA cosA]
2-D绕任意一点旋转变换矩阵是:
[x y 1] [1 0 0] [cosA sinA 0] [1 0 0] [x' y' -]
[0 1 0] x [0 1 0] x [-sinA cosA 0] x [0 1 0] = [- - -]
[0 0 1] [rtx rty 1] [0 0 1] [-rtx -rty 1] [- - -]
(2):利用Ransac算法进行拟合
http://www.cnblogs.com/xrwang/archive/2011/03/09/ransac-1.html
作者:王先荣
本文翻译自维基百科,英文原文地址是:http://en.wikipedia.org/wiki/ransac,如果您英语不错,建议您直接查看原文。
RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。该算法最早由Fischler和Bolles于1981年提出。
RANSAC的基本假设是:
(1)数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
(2)“局外点”是不能适应该模型的数据;
(3)除此之外的数据属于噪声。
局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设。
RANSAC也做了以下假设:给定一组(通常很小的)局内点,存在一个可以估计模型参数的过程;而该模型能够解释或者适用于局内点。
本文内容
1 示例
2 概述
3 算法
4 参数
5 优点与缺点
6 应用
7 参考文献
8 外部链接
一、示例
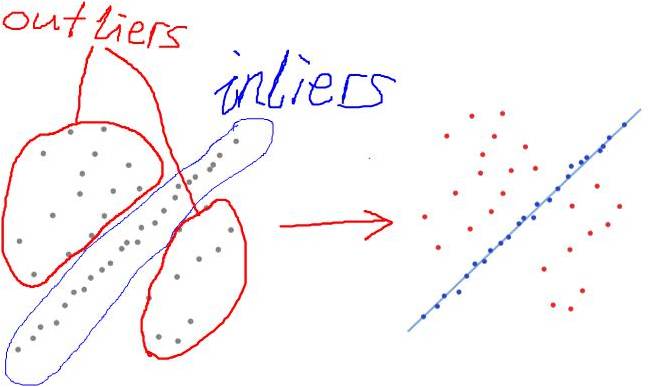
一个简单的例子是从一组观测数据中找出合适的2维直线。假设观测数据中包含局内点和局外点,其中局内点近似的被直线所通过,而局外点远离于直线。简单的最小二乘法不能找到适应于局内点的直线,原因是最小二乘法尽量去适应包括局外点在内的所有点。相反,RANSAC能得出一个仅仅用局内点计算出模型,并且概率还足够高。但是,RANSAC并不能保证结果一定正确,为了保证算法有足够高的合理概率,我们必须小心的选择算法的参数。


左图:包含很多局外点的数据集 右图:RANSAC找到的直线(局外点并不影响结果)
二、概述
RANSAC算法的输入是一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可信的参数。
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证:
1.有一个模型适应于假设的局内点,即所有的未知参数都能从假设的局内点计算得出。
2.用1中得到的模型去测试所有的其它数据,如果某个点适用于估计的模型,认为它也是局内点。
3.如果有足够多的点被归类为假设的局内点,那么估计的模型就足够合理。
4.然后,用所有假设的局内点去重新估计模型,因为它仅仅被初始的假设局内点估计过。
5.最后,通过估计局内点与模型的错误率来评估模型。
这个过程被重复执行固定的次数,每次产生的模型要么因为局内点太少而被舍弃,要么因为比现有的模型更好而被选用。
三、算法
伪码形式的算法如下所示:
输入:
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出:
best_model —— 跟数据最匹配的模型参数(如果没有找到好的模型,返回null)
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误
iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers
for ( 每个数据集中不属于maybe_inliers的点 )
if ( 如果点适合于maybe_model,且错误小于t )
将点添加到consensus_set
if ( consensus_set中的元素数目大于d )
已经找到了好的模型,现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型,保存该模型直到更好的模型出现
best_model = better_model
best_consensus_set = consensus_set
best_error = this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error
RANSAC算法的可能变化包括以下几种:
(1)如果发现了一种足够好的模型(该模型有足够小的错误率),则跳出主循环。这样可能会节约计算额外参数的时间。
(2)直接从maybe_model计算this_error,而不从consensus_set重新估计模型。这样可能会节约比较两种模型错误的时间,但可能会对噪声更敏感。
四、参数
我们不得不根据特定的问题和数据集通过实验来确定参数t和d。然而参数k(迭代次数)可以从理论结果推断。当我们从估计模型参数时,用p表示一些迭代过程中从数据集内随机选取出的点均为局内点的概率;此时,结果模型很可能有用,因此p也表征了算法产生有用结果的概率。用w表示每次从数据集中选取一个局内点的概率,如下式所示:
w = 局内点的数目 / 数据集的数目
通常情况下,我们事先并不知道w的值,但是可以给出一些鲁棒的值。假设估计模型需要选定n个点,wn是所有n个点均为局内点的概率;1 −wn是n个点中至少有一个点为局外点的概率,此时表明我们从数据集中估计出了一个不好的模型。 (1 −wn)k表示算法永远都不会选择到n个点均为局内点的概率,它和1-p相同。因此,
1 − p = (1 − wn)k
我们对上式的两边取对数,得出
![]()
值得注意的是,这个结果假设n个点都是独立选择的;也就是说,某个点被选定之后,它可能会被后续的迭代过程重复选定到。这种方法通常都不合理,由此推导出的k值被看作是选取不重复点的上限。例如,要从上图中的数据集寻找适合的直线,RANSAC算法通常在每次迭代时选取2个点,计算通过这两点的直线maybe_model,要求这两点必须唯一。
为了得到更可信的参数,标准偏差或它的乘积可以被加到k上。k的标准偏差定义为:
![]()
五、优点与缺点
RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
六、应用
RANSAC算法经常用于计算机视觉,例如同时求解相关问题与估计立体摄像机的基础矩阵。
七、参考文献
- Martin A. Fischler and Robert C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography".Comm. of the ACM 24: 381–395. doi:10.1145/358669.358692.
- David A. Forsyth and Jean Ponce (2003). Computer Vision, a modern approach. Prentice Hall.ISBN 0-13-085198-1.
- Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge University Press.
- P.H.S. Torr and D.W. Murray (1997). "The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix".International Journal of Computer Vision 24: 271–300. doi:10.1023/A:1007927408552.
- Ondrej Chum (2005). "Two-View Geometry Estimation by Random Sample and Consensus". PhD Thesis.http://cmp.felk.cvut.cz/~chum/Teze/Chum-PhD.pdf
- Sunglok Choi, Taemin Kim, and Wonpil Yu (2009)."Performance Evaluation of RANSAC Family". In Proceedings of the British Machine Vision Conference (BMVC).http://www.bmva.org/bmvc/2009/Papers/Paper355/Paper355.pdf.
八、外部链接
- RANSAC Toolbox for MATLAB. A research (and didactic) oriented toolbox to explore the RANSAC algorithm inMATLAB. It is highly configurable and contains the routines to solve a few relevant estimation problems.
- Implementation in C++ as a generic template.
- RANSAC for Dummies A simple tutorial with many examples that uses the RANSAC Toolbox for MATLAB.
- 25 Years of RANSAC Workshop
九、后话
本文在翻译的过程中参考了沈乐君的文章《随机抽样一致性算法RANSAC源程序和教程》。Ziv Yaniv已经用C++实现了RANSAC,您可以点击这里下载源程序。
不过,如果时间允许的话,我打算自己动手用C#去实现RANSAC算法,原因有两个:
(1)熟悉算法的最佳途径是自己去实现它;
(2)方便使用.net的同志们利用RANSAC。
(4):机器视觉之 ICP算法和RANSAC算法:http://www.cnblogs.com/yin52133/archive/2012/07/21/2602562.html
(一) ICP算法(Iterative Closest Point迭代最近点)
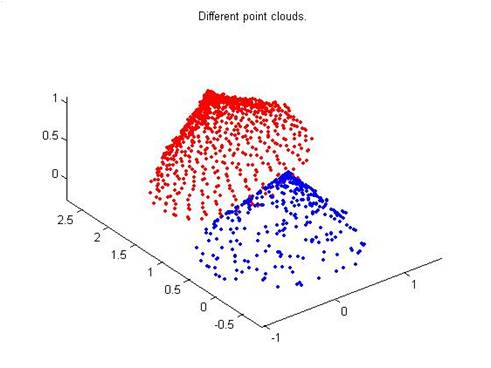
ICP(Iterative Closest Point迭代最近点)算法是一种点集对点集配准方法,如下图1
如下图,假设PR(红色块)和RB(蓝色块)是两个点集,该算法就是计算怎么把PB平移旋转,使PB和PR尽量重叠,建立模型的
ICP是改进自对应点集配准算法的
对应点集配准算法是假设一个理想状况,将一个模型点云数据X(如上图的PB)利用四元数![]() 旋转,并平移
旋转,并平移![]() 得到点云P(类似于上图的PR)。而对应点集配准算法主要就是怎么计算出qR和qT的,知道这两个就可以匹配点云了。
得到点云P(类似于上图的PR)。而对应点集配准算法主要就是怎么计算出qR和qT的,知道这两个就可以匹配点云了。
但是对应点集配准算法的前提条件是计算中的点云数据PB和PR的元素一一对应,这个条件在现实里因误差等问题,不太可能实线,所以就有了ICP算法
ICP算法是从源点云上的(PB)每个点 先计算出目标点云(PR)的每个点的距离,使每个点和目标云的最近点匹配,(记得这种映射方式叫满射吧)
这样满足了对应点集配准算法的前提条件、每个点都有了对应的映射点,则可以按照对应点集配准算法计算,但因为这个是假设,所以需要重复迭代运行上述过程,直到均方差误差小于某个阀值。
也就是说 每次迭代,整个模型是靠近一点,每次都重新找最近点,然后再根据对应点集批准算法算一次,比较均方差误差,如果不满足就继续迭代
(二)RANSAC算法(RANdom SAmple Consensus随机抽样一致)
它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。该算法最早由Fischler和Bolles于1981年提出。
光看文字还是太抽象了,我们再用图描述
RANSAC的基本假设是:
(1)数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
(2)“局外点”是不能适应该模型的数据;
(3)除此之外的数据属于噪声。
而下图二里面、蓝色部分为局内点,而红色部分就是局外点,而这个算法要算出的就是蓝色部分那个模型的参数
RANSAC算法的输入是一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可信的参数。
在上图二中 左半部分灰色的点为观测数据,一个可以解释或者适应于观测数据的参数化模型 我们可以在这个图定义为一条直线,如y=kx + b;
一些可信的参数指的就是指定的局内点范围。而k,和b就是我们需要用RANSAC算法求出来的
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证:
1.有一个模型适应于假设的局内点,即所有的未知参数都能从假设的局内点计算得出。
2.用1中得到的模型去测试所有的其它数据,如果某个点适用于估计的模型,认为它也是局内点。
3.如果有足够多的点被归类为假设的局内点,那么估计的模型就足够合理。
4.然后,用所有假设的局内点去重新估计模型,因为它仅仅被初始的假设局内点估计过。
5.最后,通过估计局内点与模型的错误率来评估模型。
这个过程被重复执行固定的次数,每次产生的模型要么因为局内点太少而被舍弃,要么因为比现有的模型更好而被选用。
这个算法用图二的例子说明就是先随机找到内点,计算k1和b1,再用这个模型算其他内点是不是也满足y=k1x+b2,评估模型
再跟后面的两个随机的内点算出来的k2和b2比较模型评估值,不停迭代最后找到最优点
我再用图一的模型说明一下RANSAC算法
RANSAC算法的输入是一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可信的参数。