NYOJ 12 喷水装置（二）

题目链接：http://acm.nyist.net/JudgeOnline/problem.php?pid=12

解题难点与思路：

1.不知道跟贪心有什么关系，于是联系到了radar（nyoj287）那道题目，发现两题有相似点，于是很快就会想到区间覆盖的题目，但是这个覆盖有点儿不同

2.知道了是区间覆盖后，但是不知道怎么满足把所有的地方都覆盖（就是选最好的区间段使得区间与区间之间没有间隙，一直到线段的最末端）。

3.贪心策略是将左端点从小到大排序，选择右端点，使得右端点尽量覆盖的最远

代码如下：

 #include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
const int MAX=10001;
struct interval{
    double left,right;
};
bool order_by_right(struct interval a,struct interval b){
        return a.left<b.left;

}
int main()
{

    int i,j,pump_num,len,wight,times,count,biaoji;
    double wight_2;
    struct interval a[MAX];
    scanf("%d",&times);
    while(times--)
    {
		biaoji=1;
        count=0;
        scanf("%d%d%d",&pump_num,&len,&wight);
        wight_2=wight/2.000000;
        for(i=0;i<pump_num;i++)
        {
            int temp_x,temp_radous;
            double temp_w;
            scanf("%d%d",&temp_x,&temp_radous);
			temp_w=sqrt(temp_radous*temp_radous-wight_2*wight_2);
			if(temp_w>0)
			{
				a[i].left=temp_x-temp_w;                 //转换成区间问题
				a[i].right=temp_x+temp_w;
			}

        }
        sort(a,a+pump_num,order_by_right);
		double Max=0; //比上一个装置及之前的装置（不是光上一个装置覆盖的长度）多覆盖的长度,一定要记住，Max是这次会阔展（只是比上一次多的长度，而不一定会是某一个区间的长度（一般不会是区间长度））的长度
		double sum=0;          //在使用本装置之前已经被覆盖的长度
		while(sum<len)
		{
			Max=0;
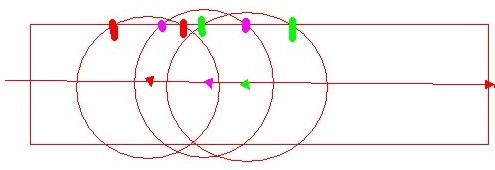
			for(i=0;i<pump_num&&a[i].left<=sum;i++) //a[i].left<=sum是为了避免最后一幅图中紫色部分中假设没有第二条线的情况
			{
				if(a[i].right-sum>Max)  //选出最后一幅图中的线段三，因为线段三可以在相接前面（不能断开）的线段的基础上覆盖的更远
				{
					Max=a[i].right-sum;
				}
			}
			if(Max==0)  //while下面初始化Max为0，就是说没有找到一个装置可以接着向后面覆盖，也就是说后面的没办法覆盖了
			{
				biaoji=0;
				break;
			}
			else
			{
				count++;
				sum+=Max;  //现在已经覆盖到了上一次覆盖到的地方加上本次又向后扩展的长度			
			}

		}
		if(biaoji)
			printf("%d\n",count);
		else
			printf("0\n");
    }
    return 0;
}