编程之美 - 光影切割问题

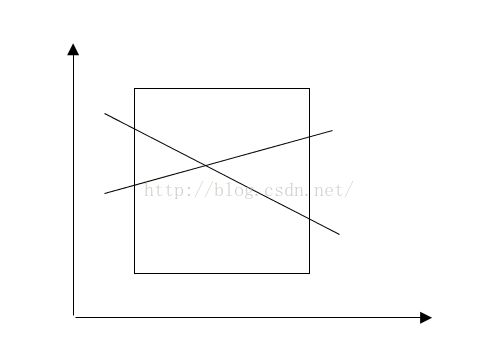
在一个平面内有一个矩形区域，直线穿过矩形可以将其分割为不同的区域，且在 这个平面中不存在三条直线相交一点的情况。求当有N条直线穿过矩形时，它被分割为多少个区域？

例如： 图中有两条直线将矩形分割为 4 个区域。

直线条数	交点个数	分割部分
1	0	2
2	1	4
2	0	3
3	0	4
3	2	6
3	3	7

由此可以看出： 分割面数 = 直线条数 + 在该区域内的交点个数

示例程序：

#include <iostream>

using namespace std;

#define TOP 9
#define RIGHT 9

typedef struct _line
{
    double _x0;
    double _y0;
    double _x1;
    double _y1;
} line_def;

// 这里采用两点式来表示直线
//line_def  test_lines[] = {{2,1,5,7},{1,2,8,4},{8,1,2,7},{8,0,4,9}};
//int test_len = 4;

//line_def  test_lines[] = {{2,1,5,7},{1,2,8,4},{8,1,2,7}};
//int test_len = 3;

line_def  test_lines[] = {{2,1,5,1},{5,5,8,5},{8,1,2,7}};
int test_len = 3;

bool find_cross(line_def line1, line_def line2, double &x, double &y)
{
    double k1 = 0, k2 = 0, b1 = 0, b2 = 0;

    if ((line1._x0 - line1._x1 != 0) && (line2._x0 - line2._x1 != 0))
    {
        k1 = (line1._y0 - line1._y1) / (line1._x0 - line1._x1);
        k2 = (line2._y0 - line2._y1) / (line2._x0 - line2._x1);

        if (k1 == k2)
            return false;

        b1 = line1._y0 - ((line1._y0 - line1._y1)/(line1._x0 - line1._x1))*line1._x0;
        b2 = line2._y0 - ((line2._y0 - line2._y1)/(line2._x0 - line2._x1))*line2._x0;

        x = (b2 - b1)/(k1 - k2);
        y = k1 * x + b1;
        return true;
    }
    else if ((line1._x0 - line1._x1 == 0) && (line2._x0 - line2._x1 == 0))
        return false;
    else if ((line1._x0 - line1._x1 == 0) && (line2._x0 - line2._x1 != 0))
    {
        x = line1._x0;
        y = (line2._y0 - line2._y1) * ((x-line2._x0)/(line2._x0-line2._x1)) + line2._y0;
    }
    else if ((line1._x0 - line1._x1 != 0) && (line2._x0 - line2._x1 == 0))
    {
        x = line2._x0;
        y = (line1._y0 - line1._y1) * ((x-line1._x0)/(line1._x0-line1._x1)) + line1._y0;
    }

    return true;
}

int calc(line_def lines[], int num)
{
    int i = 0, j = 0;
    double dx, dy;
    int cross_count = 0;
    bool bfind = false;

    for (i = 0; i < num; i++)
        for (j = i+1; j < num; j++)
        {
            bfind = find_cross(lines[i], lines[j], dx, dy);
            if (bfind && ((dx > 0) && (dx < RIGHT) && (dy > 0) && (dy < TOP)))
            {
                cout << dx << ",  " << dy << endl;
                cross_count++;
            }
        }

    cross_count += num + 1;
    return cross_count;
}

void main()
{
    int num = 0;
    num = calc(test_lines, test_len);

    cout << "\n\n==================================" << endl;
    cout << "parts: "<< num << endl;

    cin >> num;
}

总结：这个问题的关键主要是整理出点，线，面之间的数学关系，算法可以根据数学关系进行优化。