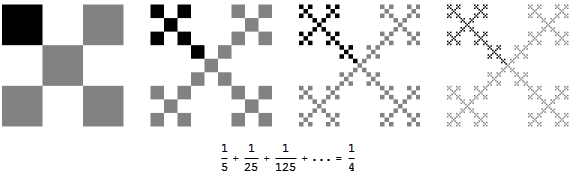有趣的分形图形-递归和数学方法解决-POJ 2083
Description
A box fractal is defined as below :
- A box fractal of degree 1 is simply
X
- A box fractal of degree 2 is
X X
X
X X
- If using B(n - 1) to represent the box fractal of degree n - 1, then a box fractal of degree n is defined recursively as following
B(n - 1) B(n - 1) B(n - 1) B(n - 1) B(n - 1)
Your task is to draw a box fractal of degree n.
Input
Output
Sample Input
1 2 3 4 -1
Sample Output
X
-
X X
X
X X
-
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
-
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
先看下较为常规的递归解决:
由于图形是重复的,小的图形只是把大图形的左上角一部分输出,,只计算最大的图形,打表可加快速度。
#include <stdio.h>
#include <string.h>
int p[8] = {1,3,9,27,81,243,729};
char map[730][730];
//n当前的图形大小,x,y图形所在的坐标
void print(int n,int x,int y){
if(n == 0){
map[x][y] = 'X'; //
return;
}
print(n-1, x, y); //左上
print(n-1, x+2*p[n-1], y); //右上
print(n-1, x+p[n-1], y+p[n-1]); //中间
print(n-1, x, y+2*p[n-1]);
print(n-1, x+2*p[n-1], y+2*p[n-1]);
}
int n;
int main(){
for(int i=0; i<p[6]; i++) memset(map[i], 32, p[6]);
print(6, 0, 0); //打表
while(scanf("%d", &n) && n-- >= 0){
for(int i=0; i<p[n]; i++){
map[i][p[n]]=0;
puts(map[i]);
map[i][p[n]]=' ';
}
puts("-");
}
return 0;
}
二 数学方法
在discuss里面看到这个短小精悍的程序。
#include"stdio.h"
#include"math.h"
main()
{
int i,j,n,ii,jj,k;
while(scanf("%d",&n)&&n--!=-1)
{
for(i=0;i<pow(3,n);i++,printf("\n"))
for(j=0;j<pow(3,n);j++)
{
for(ii=i,jj=j,k=0;k<n&&(ii%3+jj%3)%2==0;ii/=3,jj/=3,k++);
printf("%c",32+56*(k==n));
}
printf("-\n");
}
}
以下摘自 http://www.matrix67.com 博客:
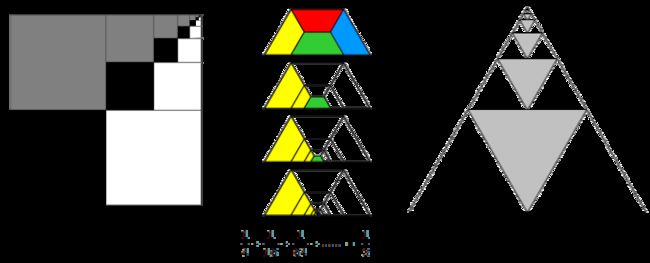
关于这个图形,还可以用来证明寻找1/5 + 1/25 + 1/125 + .. = 1/4的图形证明
前段时间,网上涌现出一大批关于1/4 + 1/16 + 1/64 + ... = 1/3的图形证明(1) (2)。不过,有多少人想过,为什么这些图形都是证明底数为1/4的情况呢?同样是几何级数求和,能否构造一个图形来证明1/5 + 1/25 + 1/125 + .. = 1/4呢?
无妨让我们来尝试一下。绝大多数人的第一想法便是画一个正五边形,然后把它分成五等分。接下来,把其中一份涂上颜色,表示整个面积的1/5。然后呢?然后怎么办?我们需要有一种办法把剩下的四块中的其中一块再次分成五份,选取一份表示1/25,并且递归地做下去。我们似乎发现了问题:这个“递归”是做不下去的。为了能够递归地表示出1/5、1/25、1/125,你必须把一个正五边形分成五个小的正五边形,再把小正五边形分成更小的五个正五边形,而这似乎是做不到的。这也就是上面的那些图形都可以用来证明Σ(1/4)^n=1/3的根本原因:它们可以把自己分成更小的四个自己,从而能够递归地表示(1/4)^n。
现在,我们的问题就出来了:为了弄出一个Σ(1/5)^n=1/4的图形证明,我们必须寻找这样一种图形,它能把自身分割为五块相同的部分,每一部分都和自身相似。
我们能否找到这样的图形呢?不能!根本原因在于:一个平面图形是二维的。平面图形的维度决定了这样一个性质:两个相似图形的相似比和面积比成平方关系。如果一个正方形的边长是另一个正方形边长的两倍,那前者的面积就是后者的四倍;圆的面积必然与半径r成平方关系,最多再乘上一个常系数。类似地,把一条曲线放大一倍,其长度也会跟着变大一倍;把一个三维图形放大一倍,其体积将变大到原来的八倍。因此,把一个平面图形分成四个和自身相似的图形是相当和谐的——面积变为原来的1/4,边长就应该变为原来的1/2,而两个1/2边长正好就拼成一个原边长。但是,如果要想把一个平面图形分成五等份,每一份的面积就应该是1/5,则对应边应该变为原来的1/sqrt(5),这样显然无法既无重复又无遗漏地填满原图形的边。看来,图形证明Σ(1/5)^n=1/4似乎就不可能了。
思考问题时要善于用想象来替代放弃。二维空间中可以证明Σ(1/4)^n=1/3。类似地,一维空间中还可以轻易证明Σ(1/2)^n=1。要是有一个什么东西是log(5)/log(2)维的就好了——这样的话,对应边扩大到原来的2倍,“面积”就会变成原来的2^(log(5)/log(2))倍,也就是5倍。这就是说,在log(5)/log(2)维的“空间”里,一个“图形”恰好可以包含5个与自身相似的“图形”,并且新的“边长”正好能整除原来的“边长”。看到这里有人会哈哈大笑起来——这种维度会有吗?
有。很多分形图形都有一些极其怪异的性质,相似比的变化和其所占空间的变化不成整次幂的关系。例如,大名鼎鼎的分形图形Sierpinski三角形就是这样——相似比为1/2,所占空间之比为1/3。一个图形有二维图形的样子,却没有二维图形的性质。Hausdorff维度就是专门用来处理这类问题的。我们常常用Hausdorff维度来描述一个分形图形,比如Sierpinski三角形的Hausdorff维度就是log(3)/log(2)——所占面积变为原来的三倍时,对应边变为原来的两倍。
嘿!那么,是不是Sierpinski三角形就可以用来证明Σ(1/3)^n=1/2呢?对!一个Sierpinski三角形由三个与自身相似的小Sierpinski三角形组成,因此你可以递归地表示出(1/3)^n。画出整个Sierpinski三角形的1/3,以及另外1/3的其中1/3,以及1/3的1/3的1/3,这样无限画下去,你会很快看出来,总区域正好占了原来的一半。
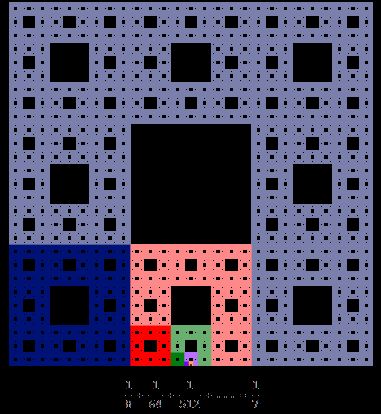
类似地,把Sierpinski地毯放大到原来的三倍,整个图形所占空间就变成了原来的八倍。它的Hausdorff维度就是log(8)/log(3)。于是,我们就能用它来证明Σ(1/8)^n=1/7。
回到本文最初的问题,为了证明Σ(1/5)^n=1/4,我们只需要找到这样一个分形图形,其Hausdorff维度的分子为log(5)。这样的图形不仅存在,而且还不止一个。大家可以在这个页面里找到各种不同Hausdorff维度的图形。我找到了一个有趣的分形图形叫做Vicsek雪花,它的Hausdorff维度是log(5)/log(3)。
不断选出更小意义上的那个1/5,你会一眼看出,选出部分的总和就是整个图形的1/4。