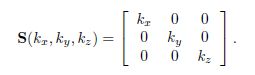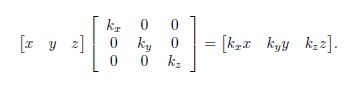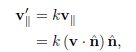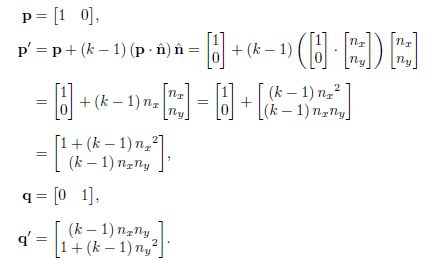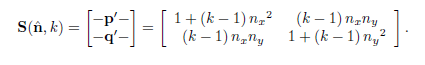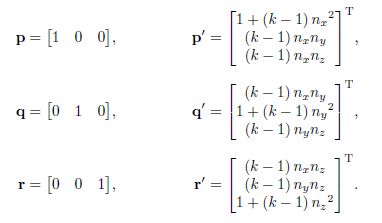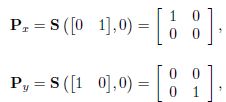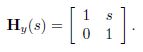沿任意方向缩放、镜像、正交投影及切变及其推导
镜像、正交投影和切变的推导都可根据缩放变形而来。在要缩放方向上去缩放因子k,如果|k|<1,物体"收缩", |k|>1,物体“膨胀”;k=0,正交投影;k<0,镜像; 切变稍有不同。
1. 缩放
01. 沿坐标轴缩放
2D中有两个缩放因子Kx和Ky,p和q是原来的基向量,缩放因子单独影响基向量,得到p`和q`:
得到缩放矩阵:
3D中增加缩放因子Kz
02.沿任意方向缩放
设n为平行于缩放方向的单位向量,k为缩放因子,缩放沿着穿过原点的并平行于n的直线(2D中)或平面(3D中)进行。
先讨论2D中的推导过程。我们需要推导一个表达式,给定向量v,可以通过v,n和k来计算v`。将v和v`分解为平行和垂直于n的分向量
![]()
v||是v在n上的投影
![]()
v⊥垂直于n,不会受缩放影响
v`||受缩放因子影响
推导得到v`
通过表达式来推导基向量
通过基向量构建矩阵,得到以单位向量n为缩放方向,以k为缩放因子的缩放矩阵
同样的原理运用在3D中
是scale(缩放)的缩写S(n,k)表示缩放矩阵
2.正交投影
投影意味和降维操作,将所有的点拉平到要投影的直线或平面上,从原来的点到投影点的直线相互平行,这就是正交投影。透视投影是另一种投影。
01. 向坐标轴或平面上投影
通过将垂直方向上缩放因子设为0来实现,如将3D点投影到xy平面,则抛弃z分量,通过将z方向上的缩放因子设为0实现。
P是projection(投影)的缩写,2D中,Px表示向x轴投影,Py同理:
3D中,Pxy表示向xy平面投影,其余同理:
02. 向任意指向或平面投影
投影有垂直于直线或平面的向量n定义,通过使n方向上的缩放因为0就能导出任意方向的投影矩阵。P(n)表示向垂直于向量n的轴或平面投影矩阵,S(n,0)表示在n方向上的缩放因子为0的缩放矩阵.
2D:
3D:
3. 镜像
也叫做反射,与正交投影相似,正交投影将缩放值k设为0,而镜像则设为-1.
R是reflect(反射)的缩写。2D:
3D:
4.切变(Shearing)
切变是坐标系的变换,非均匀的拉伸。切变时候,角度变化,但是面积或体积不变。也可以理解为坐标轴间的角度变化,造成的扭曲。
如下图,这是x坐标根据y坐标的切变,机器人的y坐标没有变化,只有x坐标变化了,变化后的坐标x`可以理解为将y坐标乘以切变因子s与原坐标x的和:x` = x + sy。如果是3D则增加z坐标的切变因子t: x` = x + sy,y` = y + tz
2D中切变矩阵为:
x坐标根据y坐标的切变
y坐标根据x坐标的切变
x,y坐标被z坐标切变