多种方式实现Sigmoid函数导数的仿真(含代码)

综述

这一周所有的空闲时间就是完成了Sigmoid函数的导数的仿真，用了总共四种方法，并对他们的性能进行了对比。并最后找到了自己的方法，想用于将来的CNN硬件代码当中。基本所有的方法都比较简单，原理我就只是大概得说一说，文章的最末尾会提供相关的参考文献（有代码了还需要其他的吗？）

方法一

在我的上面的一篇博文中介绍了一种只是用与或非门的仿真sigmoid函数的方法，下面提供了我上一篇文章的链接：[http://blog.csdn.net/xjtu_noc_wei/article/details/52886727]
这种方法可以非常快速的知道sigmoid函数的输出，然后我们可以利用sigmoid函数的特有关系即：y’=y(1-y)即可算出结果，怎么样是不是很简单呢？但是这种方法不好的地方是最后的时候使用了乘法器，然后老师就把我这个工作pass了，其实已经挺快了。直接写代码吧，二进制转换成十进制的代码我上个博文已经给出，这里直接给出核心代码：

function sig3_3_6p()
%%因为是一个小数点后面三位的二进制数
%那么000.000到111.111可以用一个十进制的最小值为0最大值为7.875，步长为0.125的数组进行表示
%v=-7.875:0.125:7.875
x=0:0.125:7.875;
m=0:-0.125:-7.875;
%fx= 1 ./ (1 + exp(- x));
fx=exp(-x)./(1+exp(-x)).^2;
%画出理想的sig函数图片
n=cell(1,size(x,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t=cell(1,size(x,2));
y=zeros(1,size(x,2));
for i=1:1:64
    [~,n{i},t{i}]=change(x(i),3);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n{i}=str2num(n{i});
    t{i}=str2num(t{i});
     x0=t{i}(3);
     x1=logical(t{i}(2));
     x2=logical(t{i}(1));
     x3=logical(n{i}(3));
     x4=logical(n{i}(2));
     x5=logical(n{i}(1));
     x_0=~x0;
     x_1=~x1;
     x_2=~x2;
     x_3=~x3;
     x_4=~x4;
     x_5=~x5;
    p1=x5&&x2;
    p2=x5&&x4;
    p3=x5&&1;
    p4=x5&&x3;
    p5=x4&&x_3&&x_2&&x_1&&x_0;
    p6=x_4&&x3&&x_2&&x_1&&x_0;
    p7=x_4&&x_3&&x2&&x1&&x_0;
    p8=x3&&x_2&&x1&&x_0;
    p9=x4&&x3&&x1&&x0;
    p10=x4&&x_3&&x1&&x0;
    p11=x4&&x2&&x1;
    p12=x_4&&x3&&x1&&x0;
    p13=x3&&x2&&x1;
    p14=x3&&x_1&&x0;
    p15=x4&&x2&&x0;
    p16=x4&&x_3&&x_2&&x1;
    p17=x_4&&x_3&&x_2&&x1;
    p18=x_4&&x3&&x2;
    p19=x4&&x3&&x2;
    p20=x_3&&x2;
    p21=x_4&&x2&&x1&&x0;
    p22=x_4&&x2&&x_1&&x0;
    p23=x4&&x_3&&x2&&x_1;
    p24=x4&&x_2&&x_1&&x0;
    p25=x_4&&x_3&&x_2&&x0;
    p26=x4&&x3;
    p27=x4&&x3&&x_2&&x_0;
    y6=1;
    y5=p3|p5|p8|p10|p11|p12|p13|p14|p15|p16|p18|p23|p24|p26;
    y4=p3|p5|p6|p10|p11|p15|p16|p20|p24|p26;
    y3=p3|p6|p11|p13|p17|p18|p21|p26;
    y2=p3|p6|p7|p9|p12|p13|p16|p19|p23|p25;
    y1=p3|p6|p7|p8|p12|p21|p22|p23|p24|p27;
    y0=p1|p2|p4|p5|p7|p8|p10|p13|p14|p15|p18|p22;
    y(i)=1/2*y6+1/4*y5+1/8*y4+1/16*y3+1/32*y2+1/64*y1+1/128*y0;
    b(i)=1-y(i);
    m(i)=y(i)*b(i);
    j=0;
    L(i)=abs(fx(i)-y(i));
    P(i)=abs(fx(i)-m(i));
    j=j+L(i);
end
   Eave=mean(P)
   Emax=max(P)
%plot(x,y,'b');
%hold on;
%plot(m,b,'b')
%hold on;
plot(x,fx,'b');
hold on;
plot(x,m,'r');
end

下面给出得出的仿真图像，还有得出的最大误差和平均误差：

方法二

这种方法怎么说呢，也就能在软件上面用用。因为用了好多乘法器还迭代了很多次，timing什么的惨不忍睹。写出来就是让大家看看，笑话笑话我。下面说一下核心算法，简单的说就是把几条直线通过迭代掰弯了。

这里面的第四行g(x)应该改成dg(x)，只是觉得真的好坑，我改了好久才改出来的！
代码如下：

function SIGD()
m=0.096225;
n=0.293391;
deta1=0.0868;
deta2=0.09634;
x=-8:0.01:8;
h=0;
dg=m.*x+n;
l=(-1)*m;
h1=l.*x+n;
fx=exp(-x)./(1+exp(-x)).^2;
q=4;
for i=0:1:q
    dg1=min(dg,h1);
    h1=0.5*(dg+h1-deta1);
    dg=max(dg1,h);
    h=0.5*(dg1+h+deta2);
    deta1=deta1/4;
    deta2=deta2/4;
end
dg1=min(dg,h1);
dg=max(dg1,h);
l=abs(dg-fx);
Emax=max(l)
Emean=mean(l)
plot(x,dg,'red');
hold on;
plot(x,fx,'b')
end

同样的，仿真图像和最大平均误差也给出了（可以看到红色的线有四条，那是q=1,2,3,4四种情形，q表示迭代次数）：


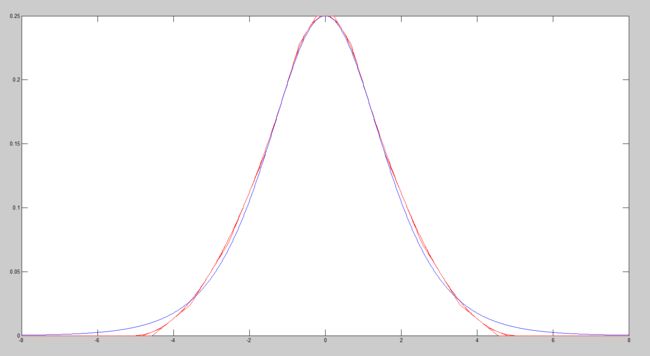
怎么样，很简单吧。

方法三

算法图如下，输入输出非常明了：

代码：

function threhold() x1=0:0.01:1;
f1=0.25;
x2=1:0.01:2;
f2=0.125;
x3=2:0.01:3;
f3=0.0625;
x4=3:0.01:4;
f4=0.03125;
x5=4:0.01:5;
f5=0.015625;
x6=5:0.01:6;
f6=0.0078125;
x7=6:0.01:7;
f7=0.00390625;
x8=7:0.01:8;
f8=0.001953125;
plot(x1,f1,'r');hold on;
plot(x2,f2,'r');hold on;
plot(x3,f3,'r');hold on;
plot(x4,f4,'r');hold on;
plot(x5,f5,'r');hold on;
plot(x6,f6,'r');hold on;
plot(x7,f7,'r');hold on;
plot(x8,f8,'r');hold on;
end

这个误差真是有点恐怖了，不在考虑范围之内。

方法四

算法：

仿真图像：

代码：

function PWL15()
input1=0:1/4096:1-1/4096;
input2=1:1/4096:2-1/4096;
input3=2:1/4096:3-1/4096;
input4=3:1/4096:4-1/4096;
input5=4:1/4096:5-1/4096;
input6=5:1/4096:6-1/4096;
input7=6:1/4096:7-1/4096;
input8=7:1/4096:8-1/4096;
n1=cell(1,size(input1,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input1,2));
y=zeros(1,size(input1,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input1(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/8+1/16+1/32+1/64*x011+1/128*x010+1/256*x09+1/512*x08+1/1024*x07+1/2048*x06+1/4096*x05+1/8192*x04+1/16384*x03+1/32768*x02;
end
plot(input1,y,'r');
hold on;
n1=cell(1,size(input2,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input2,2));
y=zeros(1,size(input2,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input2(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/8+1/32*x011+1/64*x010+1/128*x09+1/256*x08+1/512*x07+1/1024*x06+1/2048*x05+1/4096*x04+1/8192*x03+1/16384*x02+1/32768*x01;
end
plot(input2,y,'r');
hold on;
n1=cell(1,size(input3,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input3,2));
y=zeros(1,size(input3,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input3(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/16+1/32*x011+1/64*x010+1/128*x09+1/256*x08+1/512*x07+1/1024*x06+1/2048*x05+1/4096*x04+1/8192*x03+1/16384*x02+1/36728*x01;
end
plot(input3,y,'r');
hold on;
n1=cell(1,size(input4,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input4,2));
y=zeros(1,size(input4,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input4(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/64+1/128*x011+1/256*x010+1/512*x09+1/1024*x08+1/2048*x07+1/4096*x06+1/8192*x05+1/16384*x04+1/32768*x03;
end
plot(input4,y,'r');
hold on;
n1=cell(1,size(input5,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input5,2));
y=zeros(1,size(input5,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input5(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/128+1/256*x011+1/512*x010+1/1024*x09+1/2048*x08+1/4096*x07+1/8192*x06+1/16384*x05+1/32768*x04;
end
plot(input5,y,'r');
hold on;
n1=cell(1,size(input6,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input6,2));
y=zeros(1,size(input6,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input6(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/256+1/512*x011+1/1024*x010+1/2048*x09+1/4096*x08+1/8192*x07+1/16384*x06+1/32768*x05;
end
plot(input6,y,'r');
hold on;
n1=cell(1,size(input7,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input7,2));
y=zeros(1,size(input7,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input7(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/512+1/1024*x011+1/2048*x010+1/4096*x09+1/8192*x08+1/16384*x07+1/32768*x06;
end
plot(input7,y,'r');
hold on;
n1=cell(1,size(input8,2));%建立大小和x相同的胞元将数组或者数存到胞元里面
t1=cell(1,size(input8,2));
y=zeros(1,size(input8,2));
for i=1:1:4096
 [~,n1{i},t1{i}]=change(input8(i),12);
    %如果直接进行取值的话得到的结果是有问题的，因为char类型中间有两个空的字符
    %只需要将char类型转化为一个新的类型就可以了
    n1{i}=str2num(n1{i});
    t1{i}=str2num(t1{i});
     x0=t1{i}(12);
     x1=t1{i}(11);
     x2=t1{i}(10);
     x3=t1{i}(9);
     x4=t1{i}(8);
     x5=t1{i}(7);
     x6=t1{i}(6);
     x7=t1{i}(5);
     x8=t1{i}(4);
     x9=t1{i}(3);
     x10=t1{i}(2);
     x11=t1{i}(1); 
     x00=~x0;
     x01=~x1;
     x02=~x2;
     x03=~x3;
     x04=~x4;
     x05=~x5;
     x06=~x6;
     x07=~x7;
     x08=~x8;
     x09=~x9;
     x010=~x10;
     x011=~x11;
     y(i)=1/1024*x011+1/2048*x010+1/4096*x09+1/8192*x08+1/16384*x07+1/32768*x06;
end
plot(input8,y,'r');
hold on;
input=0:0.01:8;
fx=exp(-input)./(1+exp(-input)).^2;
plot(input,fx,'b');
end

怎么说呢，这个误差在我看来是难以接受的，虽然它写起来非常简单，只需要简单的移位就可以解决了。

Mysolution

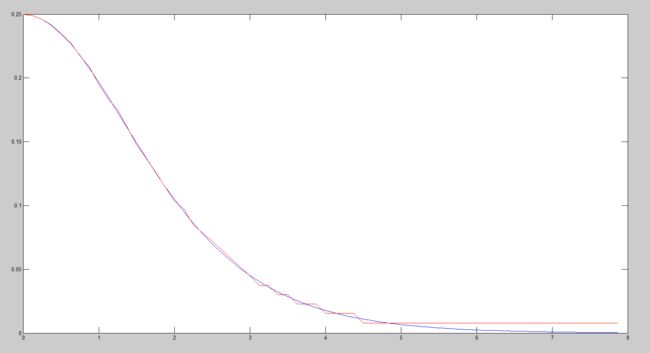
现在重点来了，在上面这几种方法的结果都不尽如人意的时候，要用什么方法来仿真呢？所以我想着对方法三进行改进，15段线确实很少。就像用正多边形接近圆一样，增加边的数量可以增加精度，那么同理，怎么仿真用的线段条数的时候会增加精度，于是我采用了128段线的方式。举个例子，就是当（0.125>x>0）时，这一段的函数值我都定义成x=0.0625时的函数值。虽然麻烦，但是仔细想想，在硬件里头，这只需要存64个浮点数就可以。恩，代码如下：

function Mysolution() x1=0:0.01:0.125;
f1=0.2498 ;
x2=0.125:0.01:0.25;
f2=0.2478;
x3=0.25:0.01:0.375;
f3= 0.2440 ;
x4=0.375:0.01:0.5;
f4=0.2384;
x5=0.5:0.01:0.625;
f5=0.2312;
x6=0.625:0.01:0.75;
f6=0.2226;
x7=0.75:0.01:0.875;
f7=0.2129;
x8=0.875:0.01:1;
f8=0.2022;
x9=1:0.01:1.125;
f9=0.1909;
x10=1.125:0.01:1.25;
f10=0.1791;
x11=1.25:0.01:1.375;
f11=0.1671;
x12=1.375:0.01:1.5;
f12=0.1551;
x13=1.5:0.01:1.625;
f13=0.1443;
x14=1.625:0.01:1.75;
f14=0.1317;
x15=1.75:0.01:1.875;
f15=0.1206;
x16=1.875:0.01:2;
f16=0.1101;
x17=2:0.01:2.125;
f17=0.1001;
x18=2.125:0.01:2.25;
f18=0.0907;
x19=2.25:0.01:2.375;
f19=0.0820;
x20=2.375:0.01:2.5;
f20=0.0739;
x21=2.5:0.01:2.625;
f21=0.0665;
x22=2.625:0.01:2.75;
f22=0.0597;
x23=2.75:0.01:2.875;
f23=0.0534;
x24=2.875:0.01:3;
f24=0.0478;
x25=3:0.01:3.125;
f25=0.0427;
x26=3.125:0.01:3.25;
f26=0.0381;
x27=3.25:0.01:3.375;
f27=0.0339;
x28=3.375:0.01:3.5;
f28=0.0302;
x29=3.5:0.01:3.625;
f29=0.0268;
x30=3.625:0.01:3.75;
f30=0.0238;
x31=3.75:0.01:3.875;
f31=0.0211;
x32=3.875:0.01:4;
f32=0.0188;
x33=4:0.01:4.125;
f33=0.0166;
x34=4.125:0.01:4.25;
f34=0.0147;
x35=4.25:0.01:4.375;
f35=0.0130;
x36=4.375:0.01:4.5;
f36=0.0116;
x37=4.5:0.01:4.625;
f37=0.0102;
x38=4.625:0.01:4.75;
f38=0.009;
x39=4.75:0.01:4.875;
f39=0.008;
x40=4.875:0.01:5;
f40=0.0071;
x41=5:0.01:5.125;
f41=0.0063;
x42=5.125:0.01:5.25;
f42=0.0055;
x43=5.25:0.01:5.375;
f43=0.0049;
x44=5.375:0.01:5.5;
f44=0.0043;
x45=5.5:0.01:5.625;
f45=0.0038;
x46=5.625:0.01:5.75;
f46=0.0034;
x47=5.75:0.01:5.875;
f47=0.0030;
x48=5.875:0.01:6;
f48=0.0026;
x49=6:0.01:6.125;
f49=0.0023;
x50=6.125:0.01:6.25;
f50=0.0020;
x51=6.25:0.01:6.375;
f51=0.0018;
x52=6.375:0.01:6.5;
f52=0.0016;
x53=6.5:0.01:6.625;
f53=0.0014;
x54=6.625:0.01:6.75;
f54=0.0012;
x55=6.75:0.01:6.875;
f55=0.0011;
x56=6.875:0.01:7;
f56=0.0010;
x57=7:0.01:7.125;
f57=0.0009;
x58=7.125:0.01:7.25;
f58=0.0008;
x59=7.25:0.01:7.375;
f59=0.0007;
x60=7.375:0.01:7.5;
f60=0.0006;
x61=7.5:0.01:7.625;
f61=0.0005;
x62=7.625:0.01:7.75;
f62=0.0005;
x63=7.75:0.01:7.875;
f63=0.0004;
x64=7.875:0.01:8;
f64=0.0004;
x=0.0625:0.125:7.9375;
fx=exp(-x)./(1+exp(-x)).^2;
plot(x,fx,'b');
hold on;
plot(x1,f1,'r');hold on;
plot(x2,f2,'r');hold on;
plot(x3,f3,'r');hold on;
plot(x4,f4,'r');hold on;
plot(x5,f5,'r');hold on;
plot(x6,f6,'r');hold on;
plot(x7,f7,'r');hold on;
plot(x8,f8,'r');hold on;
plot(x9,f9,'r');hold on;
plot(x10,f10,'r');hold on;
plot(x11,f11,'r');hold on;
plot(x12,f12,'r');hold on;
plot(x13,f13,'r');hold on;
plot(x14,f14,'r');hold on;
plot(x15,f15,'r');hold on;
plot(x16,f16,'r');hold on;
plot(x17,f17,'r');hold on;
plot(x18,f18,'r');hold on;
plot(x19,f19,'r');hold on;
plot(x20,f20,'r');hold on;
plot(x21,f21,'r');hold on;
plot(x22,f22,'r');hold on;
plot(x23,f23,'r');hold on;
plot(x24,f24,'r');hold on;
plot(x25,f25,'r');hold on;
plot(x26,f26,'r');hold on;
plot(x27,f27,'r');hold on;
plot(x28,f28,'r');hold on;
plot(x29,f29,'r');hold on;
plot(x30,f30,'r');hold on;
plot(x31,f31,'r');hold on;
plot(x32,f32,'r');hold on;
plot(x33,f33,'r');hold on;
plot(x34,f34,'r');hold on;
plot(x35,f35,'r');hold on;
plot(x36,f36,'r');hold on;
plot(x37,f37,'r');hold on;
plot(x38,f38,'r');hold on;
plot(x39,f39,'r');hold on;
plot(x40,f40,'r');hold on;
plot(x41,f41,'r');hold on;
plot(x42,f42,'r');hold on;
plot(x43,f43,'r');hold on;
plot(x44,f44,'r');hold on;
plot(x45,f45,'r');hold on;
plot(x46,f46,'r');hold on;
plot(x47,f47,'r');hold on;
plot(x48,f48,'r');hold on;
plot(x49,f49,'r');hold on;
plot(x50,f50,'r');hold on;
plot(x51,f51,'r');hold on;
plot(x52,f52,'r');hold on;
plot(x53,f53,'r');hold on;
plot(x54,f54,'r');hold on;
plot(x55,f55,'r');hold on;
plot(x56,f56,'r');hold on;
plot(x57,f57,'r');hold on;
plot(x58,f58,'r');hold on;
plot(x59,f59,'r');hold on;
plot(x60,f60,'r');hold on;
plot(x61,f61,'r');hold on;
plot(x62,f62,'r');hold on;
plot(x63,f63,'r');hold on;
plot(x64,f64,'r');hold on;
xx=0.0625:0.125:8-0.0625;
ff=exp(-xx)./(1+exp(-xx)).^2
plot(xx,ff,'black');
end

代码有点多，但是都还蛮简单的。
参考文献：神经网络激活函数及其导数的 FPGA 实现、Approximation of Sigmoid Function and the Derivative for Artificial Neurons