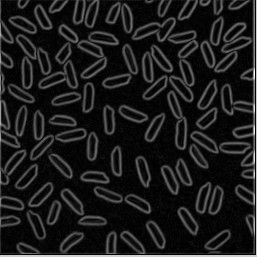
canny算子原理
转自:http://blog.csdn.net/xiajun07061225/article/details/6926108
Canny边缘检测算法一直是边缘检测的经典算法。下面详细介绍Canny边缘检测算法的原理以及编程实现。
Canny边缘检测基本原理:
(1)图象边缘检测必须满足两个条件:一能有效地抑制噪声;二必须尽量精确确定边缘的位置。
(2)根据对信噪比与定位乘积进行测度,得到最优化逼近算子。这就是Canny边缘检测算子。
(3)类似与Marr(LoG)边缘检测方法,也属于先平滑后求导数的方法。
Canny 的目标是找到一个最优的边缘检测算法,最优边缘检测的含义是:
(1)好的检测 - 算法能够尽可能多地标识出图像中的实际边缘。
(2)好的定位 - 标识出的边缘要尽可能与实际图像中的实际边缘尽可能接近。
(3)最小响应 - 图像中的边缘只能标识一次,并且可能存在的图像雜訊不应标识为边缘。
Canny边缘检测算法的步骤:
(1)去噪
任何边缘检测算法都不可能在未经处理的原始数据上很好地處理,所以第一步是对原始数据与高斯 mask 作卷积,得到的图像与原始图像相比有些轻微的模糊(blurred)。这样,单独的一个像素雜訊在经过高斯平滑的图像上变得几乎没有影响。
(2)用一阶偏导的有限差分来计算梯度的幅值和方向。
(3)对梯度幅值进行非极大值抑制。
仅仅得到全局的梯度并不足以确定边缘,因此为确定边缘,必须保留局部梯度最大的点,而抑制非极大值。(non-maxima suppression,NMS)
解决方法:利用梯度的方向。
四个扇区的标号为0到3,对应3*3邻域的四种可能组合。在每一点上,邻域的中心象素M与沿着梯度线的两个象素相比。如果M的梯度值不比沿梯度线的两个相邻象素梯度值大,则令M=0。
(4)用双阈值算法检测和连接边缘。
减少假边缘段数量的典型方法是对N[i,j]使用一个阈值。将低于阈值的所有值赋零值。但问题是如何选取阈值?
解决方法:双阈值算法。双阈值算法对非极大值抑制图象作用两个阈值τ1和τ2,且2τ1≈τ2,从而可以得到两个阈值边缘图象N1[i,j]和N2[i,j]。由于N2[i,j]使用高阈值得到,因而含有很少的假边缘,但有间断(不闭合)。双阈值法要在N2[i,j]中把边缘连接成轮廓,当到达轮廓的端点时,该算法就在N1[i,j]的8邻点位置寻找可以连接到轮廓上的边缘,这样,算法不断地在N1[i,j]中收集边缘,直到将N2[i,j]连接起来为止。
在连接边缘的时候,用数组模拟队列的实现。以进行8-连通域搜索。
更详细的资料请参考维基百科:http://zh.wikipedia.org/wiki/Canny%E7%AE%97%E5%AD%90
下面是我编程实现的Canny边缘检测代码,如有错误,请大家包涵、指正:
- I = imread('rice.png');
- I = double(I);
- [height,width] = size(I);
- J = I;
- conv = zeros(5,5);%高斯卷积核
- sigma = 1;%方差
- sigma_2 = sigma * sigma;%临时变量
- sum = 0;
- for i = 1:5
- for j = 1:5
- conv(i,j) = exp((-(i - 3) * (i - 3) - (j - 3) * (j - 3)) / (2 * sigma_2)) / (2 * 3.14 * sigma_2);%高斯公式
- sum = sum + conv(i,j);
- end
- end
- conv = conv./sum;%标准化
- %对图像实施高斯滤波
- for i = 1:height
- for j = 1:width
- sum = 0;%临时变量
- for k = 1:5
- for m = 1:5
- if (i - 3 + k) > 0 && (i - 3 + k) <= height && (j - 3 + m) > 0 && (j - 3 + m) < width
- sum = sum + conv(k,m) * I(i - 3 + k,j - 3 + m);
- end
- end
- end
- J(i,j) = sum;
- end
- end
- figure,imshow(J,[])
- title('高斯滤波后的结果')
- %求梯度
- dx = zeros(height,width);%x方向梯度
- dy = zeros(height,width);%y方向梯度
- d = zeros(height,width);
- for i = 1:height - 1
- for j = 1:width - 1
- dx(i,j) = J(i,j + 1) - J(i,j);
- dy(i,j) = J(i + 1,j) - J(i,j);
- d(i,j) = sqrt(dx(i,j) * dx(i,j) + dy(i,j) * dy(i,j));
- end
- end
- figure,imshow(d,[])
- title('求梯度后的结果')
- %局部非极大值抑制
- K = d;%记录进行非极大值抑制后的梯度
- %设置图像边缘为不可能的边缘点
- for j = 1:width
- K(1,j) = 0;
- end
- for j = 1:width
- K(height,j) = 0;
- end
- for i = 2:width - 1
- K(i,1) = 0;
- end
- for i = 2:width - 1
- K(i,width) = 0;
- end
- for i = 2:height - 1
- for j = 2:width - 1
- %当前像素点的梯度值为0,则一定不是边缘点
- if d(i,j) == 0
- K(i,j) = 0;
- else
- gradX = dx(i,j);%当前点x方向导数
- gradY = dy(i,j);%当前点y方向导数
- gradTemp = d(i,j);%当前点梯度
- %如果Y方向幅度值较大
- if abs(gradY) > abs(gradX)
- weight = abs(gradX) / abs(gradY);%权重
- grad2 = d(i - 1,j);
- grad4 = d(i + 1,j);
- %如果x、y方向导数符号相同
- %像素点位置关系
- %g1 g2
- % C
- % g4 g3
- if gradX * gradY > 0
- grad1 = d(i - 1,j - 1);
- grad3 = d(i + 1,j + 1);
- else
- %如果x、y方向导数符号反
- %像素点位置关系
- % g2 g1
- % C
- %g3 g4
- grad1 = d(i - 1,j + 1);
- grad3 = d(i + 1,j - 1);
- end
- %如果X方向幅度值较大
- else
- weight = abs(gradY) / abs(gradX);%权重
- grad2 = d(i,j - 1);
- grad4 = d(i,j + 1);
- %如果x、y方向导数符号相同
- %像素点位置关系
- %g3
- %g4 C g2
- % g1
- if gradX * gradY > 0
- grad1 = d(i + 1,j + 1);
- grad3 = d(i - 1,j - 1);
- else
- %如果x、y方向导数符号反
- %像素点位置关系
- % g1
- %g4 C g2
- %g3
- grad1 = d(i - 1,j + 1);
- grad3 = d(i + 1,j - 1);
- end
- end
- %利用grad1-grad4对梯度进行插值
- gradTemp1 = weight * grad1 + (1 - weight) * grad2;
- gradTemp2 = weight * grad3 + (1 - weight) * grad4;
- %当前像素的梯度是局部的最大值,可能是边缘点
- if gradTemp >= gradTemp1 && gradTemp >= gradTemp2
- K(i,j) = gradTemp;
- else
- %不可能是边缘点
- K(i,j) = 0;
- end
- end
- end
- end
- figure,imshow(K,[])
- title('非极大值抑制后的结果')
- %定义双阈值:EP_MIN、EP_MAX,且EP_MAX = 2 * EP_MIN
- EP_MIN = 12;
- EP_MAX = EP_MIN * 2;
- EdgeLarge = zeros(height,width);%记录真边缘
- EdgeBetween = zeros(height,width);%记录可能的边缘点
- for i = 1:height
- for j = 1:width
- if K(i,j) >= EP_MAX%小于小阈值,不可能为边缘点
- EdgeLarge(i,j) = K(i,j);
- else if K(i,j) >= EP_MIN
- EdgeBetween(i,j) = K(i,j);
- end
- end
- end
- end
- %把EdgeLarge的边缘连成连续的轮廓
- MAXSIZE = 999999;
- Queue = zeros(MAXSIZE,2);%用数组模拟队列
- front = 1;%队头
- rear = 1;%队尾
- edge = zeros(height,width);
- for i = 1:height
- for j = 1:width
- if EdgeLarge(i,j) > 0
- %强点入队
- Queue(rear,1) = i;
- Queue(rear,2) = j;
- rear = rear + 1;
- edge(i,j) = EdgeLarge(i,j);
- EdgeLarge(i,j) = 0;%避免重复计算
- end
- while front ~= rear%队不空
- %队头出队
- temp_i = Queue(front,1);
- temp_j = Queue(front,2);
- front = front + 1;
- %8-连通域寻找可能的边缘点
- %左上方
- if EdgeBetween(temp_i - 1,temp_j - 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i - 1,temp_j - 1) = K(temp_i - 1,temp_j - 1);
- EdgeBetween(temp_i - 1,temp_j - 1) = 0;%避免重复计算
- %入队
- Queue(rear,1) = temp_i - 1;
- Queue(rear,2) = temp_j - 1;
- rear = rear + 1;
- end
- %正上方
- if EdgeBetween(temp_i - 1,temp_j) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i - 1,temp_j) = K(temp_i - 1,temp_j);
- EdgeBetween(temp_i - 1,temp_j) = 0;
- %入队
- Queue(rear,1) = temp_i - 1;
- Queue(rear,2) = temp_j;
- rear = rear + 1;
- end
- %右上方
- if EdgeBetween(temp_i - 1,temp_j + 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i - 1,temp_j + 1) = K(temp_i - 1,temp_j + 1);
- EdgeBetween(temp_i - 1,temp_j + 1) = 0;
- %入队
- Queue(rear,1) = temp_i - 1;
- Queue(rear,2) = temp_j + 1;
- rear = rear + 1;
- end
- %正左方
- if EdgeBetween(temp_i,temp_j - 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i,temp_j - 1) = K(temp_i,temp_j - 1);
- EdgeBetween(temp_i,temp_j - 1) = 0;
- %入队
- Queue(rear,1) = temp_i;
- Queue(rear,2) = temp_j - 1;
- rear = rear + 1;
- end
- %正右方
- if EdgeBetween(temp_i,temp_j + 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i,temp_j + 1) = K(temp_i,temp_j + 1);
- EdgeBetween(temp_i,temp_j + 1) = 0;
- %入队
- Queue(rear,1) = temp_i;
- Queue(rear,2) = temp_j + 1;
- rear = rear + 1;
- end
- %左下方
- if EdgeBetween(temp_i + 1,temp_j - 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i + 1,temp_j - 1) = K(temp_i + 1,temp_j - 1);
- EdgeBetween(temp_i + 1,temp_j - 1) = 0;
- %入队
- Queue(rear,1) = temp_i + 1;
- Queue(rear,2) = temp_j - 1;
- rear = rear + 1;
- end
- %正下方
- if EdgeBetween(temp_i + 1,temp_j) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i + 1,temp_j) = K(temp_i + 1,temp_j);
- EdgeBetween(temp_i + 1,temp_j) = 0;
- %入队
- Queue(rear,1) = temp_i + 1;
- Queue(rear,2) = temp_j;
- rear = rear + 1;
- end
- %右下方
- if EdgeBetween(temp_i + 1,temp_j + 1) > 0%把在强点周围的弱点变为强点
- EdgeLarge(temp_i + 1,temp_j + 1) = K(temp_i + 1,temp_j + 1);
- EdgeBetween(temp_i + 1,temp_j + 1) = 0;
- %入队
- Queue(rear,1) = temp_i + 1;
- Queue(rear,2) = temp_j + 1;
- rear = rear + 1;
- end
- end
- %下面2行用于观察程序运行的状况
- i
- j
- end
- end
- figure,imshow(edge,[])
- title('双阈值后的结果')
对图片rice.png进行处理后的 结果 如下: