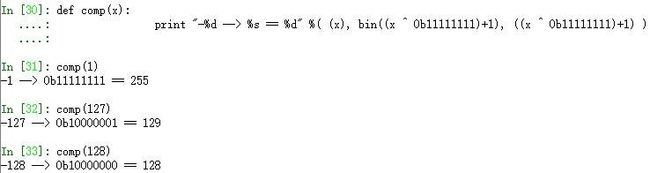A004-补码-(ques=1)
今天看到《C语言深度解剖》里面讲负数存储用补码,一时就补习一下求补码。
于是看到一篇很好的文章,它把补码用数学方式进行表达。
读完了《编码-隐匿在计算机软硬件背后的语言》(csdn下载),总算知道了计算机为什么使用补码:为了使用加法器做减法。
---------------------------------------------------------------------------------------------------------------------------------------
补码的第一种定义( 数学定义 ):
以8位宽度为例,已知一个数 X,其 8 位字长的补码定义为:
....................| X; 0 <= X <= +127 ;(也就是说:正数和0的补码,就是该数字本身)
X的补码 = |
....................| 2^8 -|X|; -128 <= X < 0 ; (也就是说:8bit负数的补码,就是用 1 0000 0000,减去该数字的绝对值)
当然,补码求反码的定义也是和这里定义的补码的一样。
他举了例子:
例如 X = -126,其补码为 1000 0010,计算方法如下:
1 0000 0000
- 0111 1110
-----------
1000 0010
应用补码进行运算:
用补码计算:83-25=58。
83 ---都变成补码,再用加法运算--> 0101 0011
- 25 -> 1 0000 0000 - 0001 1001-> + 1110 0111
----- --------
58 <--忽略进位1,结果就是正确的--[1] 0011 1010
用这个定义求出-128的补码是0b10000000。
---------------------------------------------------------------------------------------------------------------------------------------
补码的第二种定义( 机器步骤定义 ):
这个定义和平常见到的求补码的结果一致。
平时求补码的步骤:
....................| 正数和0的补码,就是该数字本身
X的补码 = |
....................| 负数的补码,等于X的反码(符号位不求反) + 1(符号位参与运算),
当然,补码求反码的定义也是和这里定义的补码的一样。
用这个定义求不出-128的补码,因为-128的原码就是9bit了,超出8bit了。
这个问题将在下面的描述中得以解决。
---------------------------------------------------------------------------------------------------------------------------------------
补码在计算机内部的状况
上面给出了求补码的2种方法,下面讲讲计算机使用补码的原因:在加法器上、使用补码来实现减法。
首先、减法会涉及到负数,因为对于A - B,我们将其视为:A + (-B) = A + C,C = -B。
使用Python计算补码、转化数值进制,让我较为容易地完成了下面的内容:
// 求 -x 补码(正数不用求补码)
def comp(x):
print "-%d --> %s == %d" %( (x), bin((x ^ 0b11111111)+1), ((x ^ 0b11111111)+1) )
用
comp(x)求出
-x 的补码,并显示该补码的
二进制形式和
十进制形式
例如:
这里求出的-127的补码是0b10000001,而0b10000001这个数的十进制是129。
可以对照下面给出的补码表,可以看出这里得到的-1、-127、-128的补码都是对的。
负数怎么表示
1、在8位宽度下,我们可以表示的二进制数的范围是[0b00000000,0b11111111] (用闭区间表示)。
也就是十进制的0-255,这可以直接用来表示为0-255的正数。
为了表示负数,人们想出了一个方法:用bit7表示正负号(1表示负数,0表示正数),bit6-bit0表示具体的数值(绝对值)。
也就是说、只能将0-255这256个数字切为两半,将8位有符号数人为的规定为:
所以负数的范围就是[-128,127],这个规定(表示法)在用补码实现减法时会用到。
(如果表示为了使用加法器来实现减法(比如如果成本低、直接再做一个减法器),也许就不需要用补码了吧)
负数怎么存储
1、人们设计了负数的表示法之后,在内存中的一个数值到底是负数还是正数,怎么区分呢。
其实不管什么数据,内存中的数值都是一串二进制。
而这串二进制代表正数还是负数、甚至是字符还是图片、亦或是一个控制状态,都只有用户自己的程序才能解释。
所以0b10000001是-127还是+129,是写程序的人自己才知道,计算机只知道这只是一串二进制编码:0b10000001。
如果我们将0b10000001从内存中读出来,就需要指定这个数值是正数还是负数,C语言中用的就是int和unsigned int等。
同样,要保存一个数值 0b10000001,可以使用 int和 unsigned int等 显式的说明这个数值是正数还是负数。也可以不说明,只要你的程序可以处理,甚至于你将0b10000001看做字符串来存储也可以,这样能减少存储空间。
只是处理的时候需要先将它转换为字符串,这一切都是程序自己处理,计算机只知道这只是一串二进制编码:0b10000001。
使用补码在加法器上实现减法
1、怎样使用补码、来让加法器做出减法的 结果 呢。
先看怎么用补码来让加法实现减法。
我们还得先知道加法的实现,下面是加法器:
这是一个8位加法器,数据部分只有低8位有效。
如果数据溢出,第9位CO就为1,CI是进位输入。
加法执行结果为:和输出 S = A + B + CI,CO=溢出状态。
加256溢出:
在8位宽度下,正数数据的范围是0-255。
如果B = 255、CI = 1,于是,S= A + B + CI 就相当于S = A + 256,结果是S = A,CO = 1。
结果有溢出,但数据部分没变。
也就是说、8位的加法器中有:A + 256 = A,超过8位部分不会体现在低8位上、只是将进位输出CO=1(第9位)而已。
也就是说 A = A + 256,加上256之后、8位加法器只是进位输出CO变成了1,具体输出数据S没有变化,这一点很重要。
将减法转换为加法:
有了上面的结果:A = A + 256 ,我们可以得到下面的结果:
A - B = (A - B) + 256 = A + ((255 - B) + 1),其中(255 - B) + 1被规定为B的补码,结果溢出:CO=1。
所以减法" A - B "就等价于加法" A + "B的补码" ",将256拆为255 + 1,是因为我们只能处理8位以内的数值。
同时、(255 - B)=0b11111111 - B,正好就是将B按位取反(反码),硬件上可以用异或门来实现这个操作。
这就是补码的出处。
我们看到、上面用来表示负数的表格中,负数部分正好可以由该负数的绝对值求补码得到。
所以说、负数是以绝对值的补码形式存在,并且和减法耦合起来。
这里只是数学上表明:使用补码、可以将减法转换为加法来实现。
我们举先两个例子来验证 A - B = A + (255 - B) + 1,然后再看看CPU的硬件上是如何实现的。
第一个例子:0x45 - 0x34 = 0x45 + (0xFF - 0x34) + 0x01 = 0x111 = 0x100 + 0x11。
0x100表示第9位CO=1,低8位等于0x11,,正好等于0x45 - 0x34。
这里留意:0x45 > 0x34,那么0x45 - 0x34使用补码运算、可以得到正确的结果0x11,但进位输出CO=1。
第二个例子:0x34- 0x45 = 0x34 + (0xFF - 0x45) + 0x01 = 0xEF = 0x000 + 0xEF。
0x000表示第9位CO=0,低8位等于0xEF = 0b11101111、bit7=1、说明是负数,这就是我们在上面先将负数的原因。
我们需要查阅上面表示负数的表格,得到0b11101111这个负数的具体值为-17 = -0x11,正好等于0x34 - 0x45。
这里留意:0x34 < 0x45,那么0x34 - 0x45使用补码运算,也可以得到正确的结果-0x11,但进位输出CO=0。
也就是说、对于A - B,使用补码与加法来实现的减法,确实可以得到正确的数值。
同时如果A > B,结果为正数,CO=1;如果A < B,结果为负数(有借位),CO=0。
结果的正负号正好和CO的数值相反,我们可以将CO取反后、用来表示结果的正负。
同时CO取反后也正好表示结果是否有借位。
这个借位也正好表明:执行减法后、CO就是判断两个数的大小的依据,可以用来实现条件跳转。
加减法器
这是一个8位加减法器,可以执行加法和减法。
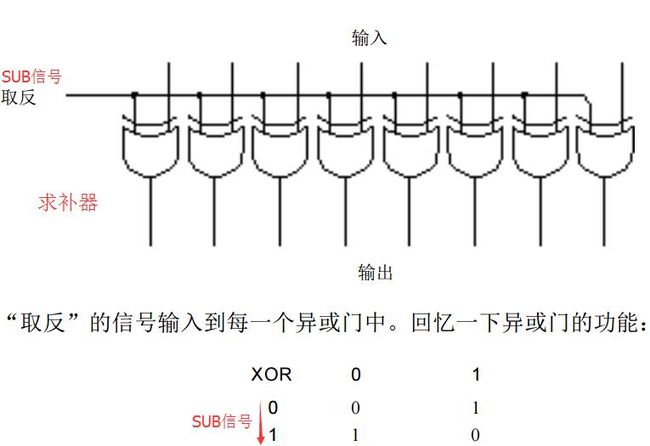
求补器实现的其实只有取反:
图中 SUB是减法的控制信号,执行减法时、 减法指令会设置 信号SUB=1, B端输入经过 求补器得到 B的"反码"( 按位取反)。同时、加法器的进位输入端CI=SBU=1,在执行加法过程中会将这个1加进去实现"反码+1",最终得到补码。
这就是补码的硬件实现。
CO经过左下角的异或门取反(在SBU=1时被取反)来得到借位信号。
而在加法过程中,SUB=0,B的按位取反和CO的取反都不会被执行,这就保持了加法的输入和结果。
这就在硬件上实现了减法:S = A - B = A + "B的补码",CO取反后表示借位,同时还不影响加法的结果和加法的进位CO。
所以说、这个结构就是加减法器。
因此、我们看到了补码的来源、和补码在负数表示和减法实现中的作用。
---------------------------------------------------------------------------------------------------------------------------------------
6种负数的加减运算
下面举例说明以下6种负数参与的加减法、都可以在补码下、通过加法器实现:
1、无符号数 - 无符号数
2、无符号数 - 负数(有符号数)
3、无符号数 + 负数(有符号数)
4、(有符号数)负数 - 无符号数
5、负数(有符号数) + 负数(有符号数)
6、负数(有符号数) - 负数(有符号数)
重点在于:执行sub(减法)时、会对减数执行求补码操作,而add(加法)则不需要。
留意到有符号数和无符号数进行运算得到的进位和借位,目前只理解两个无符号数之间的加减法的进位和借位,
有负数(有符号数)参与的运算、还不理解 进位和借位 意义。
--question-01
1、 无符号数 - 无符号数
uint8_t a = 4; uint8_t b = 3; a - b = 4 - (3); --sub指令 过程如下: 内存中的4 = 00000100 内存中的3 = 00000011 3取反 = 11111100 再加1 = 11111101 与4相加 + 00000100 结果 = 1 00000001 = 0x01,借位 = !bit9 = !1 = 0,即无借位
2、 无符号数 - 负数(有符号数)
uint8_t a = 4; int8_t b = -3; a - b = 4 - (-3); --sub指令 过程如下: 内存中的 4 = 00000100 内存中的-3 = 11111101 -3取反 = 00000010 再加1 = 00000011 与4相加 + 00000100 结果 = 0 00000111 = 7,借位 = !bit9 = !0 = 1,即有借位
3、 无符号数 + 负数(有符号数)
uint8_t a = 4; int8_t b = -3; a + b = 4 + (-3); --add指令 过程如下: 内存中的 4 = 00000100 内存中的-3 = 11111101 两者相加 = 1 00000001 = 0x01,进位 = bit9 = 1,即有进位
4、 (有符号数)负数 - 无符号数
uint8_t a = 4; int8_t b = -3; b - a = (-3) - 4; --sub指令 过程如下: 内存中的-3 = 11111101 内存中的 4 = 00000100 4取反 = 11111011 再加1 = 11111100 与-3相加 + 11111101 结果 = 1 11111001 = -7,借位 = !bit9 = !1 = 0,即无借位
5、 负数(有符号数) + 负数(有符号数)
int8_t a = -4; int8_t b = -3; b + a = (-3) + (-4); --add指令 过程如下: 内存中的-4 = 11111100 内存中的-3 = 11111101 相加 = 1 11111001 = -7,借位 = bit9 = 1,即有进位
6、 负数(有符号数) - 负数(有符号数)
int8_t a = -4; int8_t b = -3; b - a = (-3) - (-4); --sub指令 过程如下: 内存中的-3 = 11111101 内存中的-4 = 11111100 -4取反 = 00000011 再加1 = 00000100 与-3相加 + 11111101 结果 = 1 00000001 = 0x01,借位 = !bit9 = !1 = 0,即无借位
---------------------------------------------------------------------------------------------------------------------------------------
16位加减法
1、有了上面的基础、现在可以讨论16位的加减法了,其实主要是16位减法的讨论。
16位加法
1、如果没有溢出:例如0x1234 + 0x2345。
我们先用8位加法器完成低8位的运算(CI = 0):0x34 + 0x45 +CI = 0x79,CO=0。
将0x79存放到结果的低8位,并将进位CO=0在状态寄存器STATUS中的C位上保存下来。
CPU中都有一个状态寄存器STATUS,里面保存着进位C和借位S等数据。
再用8位加法器完成高8位的运算,并将低8位的进位CO放入CI(CI = CO= 0):0x12 + 0x23 + CI = 0x35,CO=0。
最后将0x35存放到结果的高8位。
结果0x3579正式0x1234 + 0x2345的正确结果,进位CO=0。
2、如果有溢出:例如0x98AC + 0xC061。
我们先用8位加法器完成低8位的运算(CI = 0):0xAC + 0x61 + CI = 0x10D = 0x100 + 0x0D,CO=1。
我们将0x0D存放到结果的低8位,并将进位CO=1在状态寄存器STATUS中的C位上保存下来。
再用8位加法器完成高8位的运算,并将低8位的进位CO输入CI (CI = CO= 1):0x98 + 0xC0 + CI = 0x159 = 0x100 + 0x59,
CO=1,最后将0x59存放到结果的高8位,结果有溢出CO=1。
结果 0x590D正式 0x98AC + 0xC061的正确结果, 进位CO=1。这个结果中:16位范围内的结果是对的,至于要不要处理进位,程序需要自己决定。
3、高8位的运算需要使用到进位CO,而低8位的运算不需要使用进位CO。
这个差异导致加法指令有两种:不带进位的加法ADD、和带进位的加法ADDC。
它们的区别就是对于CO部分的控制信号不同:是否产生控制CI=CO的控制信号。
在汇编上、使用8位加法器(8位单片机等)实现16位加法的代码,就是第1次使用ADD指令完成两个低8位的相加,
第2次使用ADDC指令完成两个高8位和CO的相加。
4、32位的加法、当然可以按照16位的实现方法、依葫芦画瓢来实现。
16位减法
1、如果没有借位:例如0x2345 - 0x1234 = 0x2345 + "0x1234的补码" = 0x2345 + "0x1234的反码" + 1。
我们先用8位加法器完成低8位的运算(CI = SUB = 1):
0x45 - 0x34 = 0x45 + "0x34的反码" +CI = 0x45 + 0xCB +1 = 0x111 = 0x100 + 0x11,CO=1。
将0x79存放到结果的低8位,并将进位CO=1在状态寄存器STATUS中的S位保存下来,借位S=!CO=0,表示没有借位。
再用8位加法器完成高8位的运算(CI = SUB = 1)(借位先不处理):
0x23 - 0x12 = 0x23 + "0x12的反码" + CI = 0x23 + 0xED + 1 = 0x111 = 0x100 + 0x11,CO=1。
最后将0x35存放到结果的高8位,借位S=!CO=0。
说明借位S=0的时候、不需要将借位纳入运算中。
2、如果有借位:例如0x1234 - 0x2345 = 0x1234 - "0x2345的反码" + 1。
我们先用8位加法器完成低8位的运算(CI = SUB = 1):
0x34 - 0x45 = 0x34 + "0x45的反码" +CI = 0x34 + 0xBA +1 = 0xEF,CO=0,0xEF是负数-0x6F。
将0xEF存放到结果的低8位,并将进位CO=0在状态寄存器STATUS中的S位保存下来,借位S=!CO=1,表示有借位。
再用8位加法器完成高8位的运算(CI = SUB = 1)(借位先不处理):
0x12 - 0x23 = 0x12 + "0x23的反码" + CI = 0x12 + 0xDC + 1 = 0xEF,CO=0。
最后将0x35存放到结果的高8位,借位S=!CO=1。
但0x1234 - 0x2345正确的结果应是-0x1111,对应的补码是0xEEEF。
所以高8位需要再减去借位S=1:0xEF - 1 = 0xEE,这个操作可以使用CPU中的减1模块来实现。
这个调用减1模块的实现、就可以通过在带借位减法指令SBB中增加响应的控制信号来实现。
(具体实现还不清楚、这是我自己想的实现方式)。
普通的减法指令SUB的控制信号中、就没有用于实现减1操作的控制信号。
最后完成了减1运算的结果是0xEEEF(补码),这个数值存放到内存中,表示一个负数(-0x1111)。
3、32位的加法过程同样可以拆分为4个8位来实现。
汇编上就是、第一次使用普通减法SUB,后三次使用带借位减法SBB。
4、小结
一般的CPU内部只有一个加法器,在这个加法器的基础上增加一个求补器得到减法器。
乘法用多次加法或向左移位来实现,除法用多次减法或向右移位来实现。
---------------------------------------------------------------------------------------------------------------------------------------