Barnes-Hut算法（quad-tree的一个应用）

Barnes-Hut算法是一种用于实现N体问题（n-body）模拟的近似算法，该算法由Josh Barnes 和 Piet Hut在1986年提出（可以参加文献【3】）。N体问题是指找出已知初始位置、速度和质量的多个物体在经典力学情况下的后续运动。庞加莱（Henri Poincaré）在研究N体问题时，发现了混沌现象。

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。

算法介绍

因为N体问题是一种混沌现象，物体未来的运动状态是没有规律可言的，所以N体模拟只能采用Brute Force的策略。一种提升N体问题模拟算法的速度，一种非常重要的思想就是把相互接近的一组物体近似看成单独的一个物体。对于一组距离足够远的物体，我们可以将它的万有引力作用近似看成是其质心的作用。一组物体的质心是这种物体经过质量加权后的平均位置。更正式地说，如果两个物体的位置分别是( x1,y1 )和( x2,y2 )，质量分别为 m1 和 m2 ，那么它们的总质量和总质心( x,y )分别为：

m=m1+m2

x=x1×m1+x2×m2m

y=y1×m1+y2×m2m

Barnes-Hut算法提供了一种将距离足够近的物体整合成一组的非常明智的方案。它递归地将物体集合分成若干组，这一个过程是通过将这些物体用四叉树（quad-tree）进行组织来实现的。注意本文主要讨论2D平面上的情况，对于3D空间中的情况，则需要使用octtree。具体来说，一棵四叉树是通过将平面不断递归地划分成四个小区域来构建的。如果一个小区域中不包含任何物体，那么这个小矩形在接下来的划分过程中就不做处理。对于那些仅包含一个物体的矩形，它在树中就会变成一个叶子节点。所有其余的小矩形则会被进一步的划分。所以这种子区域的划分最终将建造一棵非完全的树，也就是说树中每个节点最多有4个孩子，且树中的叶子节点含有且仅含有一个物体。如图所示是一个简单的例子。

我们把上图所示的物体分布情况用一个四叉树来表示即得到下图，可见每一个叶子节点都表示一个单独的物体。每一个非叶子节点都表示一组相近的物体，并且存有其所有孩子物体的总质量和质心。



如果要计算某个单独的物体所受到的合力，那么就从根开始遍历树中的节点。如果一个非叶子节点的质心离某个物体足够远，那么就将树中那个部分所包含的物体近似看成一个整体，其位置就是整组物体的质心，其质量就是整组物体的总质量。这个算法相当高效，因为我们无需逐一地单独检验某一组中的个别物体。

如果非叶子节点离某个物体并不足够远，那么就递归地遍历其所有子树。为了确定一个节点是否离得足够远，我们需要计算商 s/d , 其中 s 是非叶子节点所代表的区域的宽度， d 是物体到节点所代表的那一组物体的质心的距离。然后将这个比值同一个阈值 θ 来作比较. 如果 s/d<θ ，那么非叶子节点就足够远。通过调整参数 θ ，我们就可以来改变模拟的精度和速度。通常在实际中 θ = 0.5 是一个常常被使用的值。注意到如果 θ = 0，那么算法就退化到了使用Brute Force时的情况。

构建Barnes-Hut树

为了构建一棵Barnes-Hut树，我们将一个一个地向树中插入节点。具体来说，当向一个由（根）节点 x 所表示的树中插入一个物体 b 时，我们就递归地执行如下步骤（注意这里我们给“根”字加了一个括号的意思是即使在整棵树中某个节点不是根节点，它也可能是其中某个子树的根节点）：

1. 如果（根）节点 x 不包含物体，则把新的物体 b 放入其中。
2. 如果（根）节点 x 是一个内部节点（即非叶子节点），就更新 x 的总质量和质心。递归地将物体 b 插入到四个象限（或称分叉）中的某个。
3. 如果（根）节点 x 是一个外部节点（即叶子节点），它包含有一个物体 c ，那么也就是说在一个相同的区域里包含有两个物体 b 和 c 。那么就把这个区域进一步划分成四个子区域。然后递归地插入物体 b 和 c 到对应的分叉中。因为 b 和 c 可能仍然位于相同的子区域中，因此在一个单独的插入操作中可能涉及多个子区域划分。最终更新节点 x 的质心和总质量。

下面这个例子演示了构建一棵包含5个节点的Barnes-Hut的过程，我们按A，B，C，D，E的顺序插入节点。

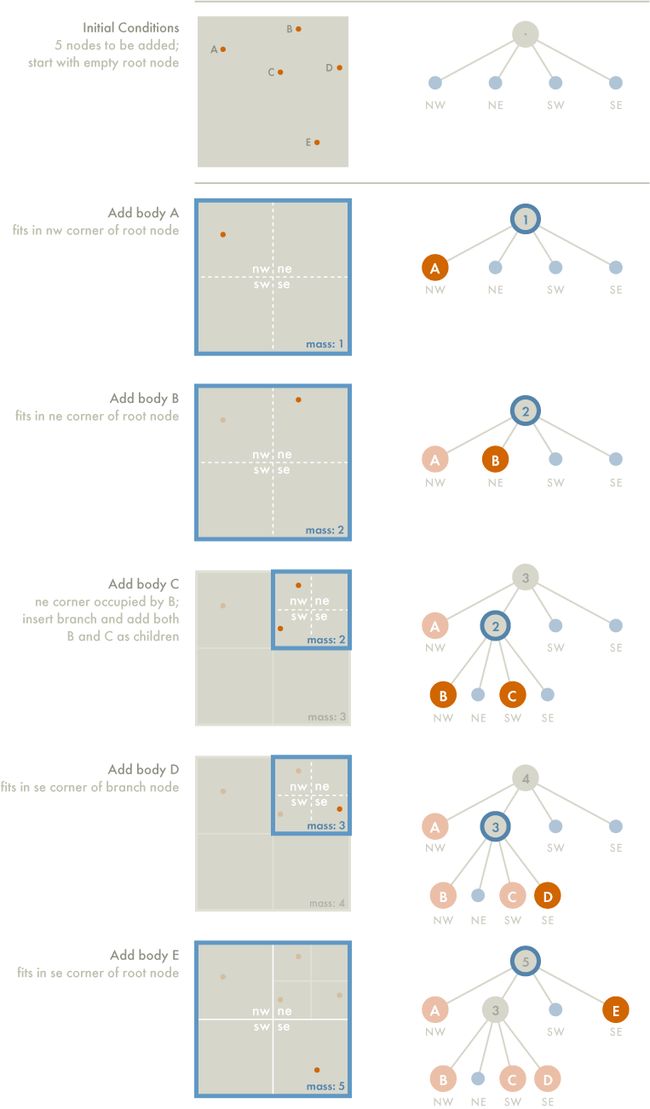
可见，根节点中储存了全部5个物体的质心和总质量。另外一个内部节点则包含有 b 、 c 和 d 三个物体所构成的整体的总质量和质心。

计算在某个物体上的作用力

为了计算某个物体 b 所受到的合力，我们需要从四叉树的根节点开始，递归地执行如下步骤：

1. 如果当前节点是一个外部节点（而且它不是物体 b ），计算当前节点施加在物体 b 上的力，并将其加到 b 的合力上。
2. 否则，计算商 s/d 的值。如果 s/d<θ ，将这个内部节点看成一个单独的物体，计算其施加在物体 b 上的力，并将其加到 b 的合力上。
3. 否则，在当前节点的每个孩子节点上递归地执行上述步骤。

我们还是来看一个例子。我们计算在物体 a 上的合力，我们从根节点开始，它是一个内部节点，包含了 A,B,C,D,E,F 六个物体的质心，这六个物体的质量分别为 1,2,3,4,5,6 千克。

我们首先检测根节点，将区域宽度 s 和物体A到当前节点（根节点）的质心（图中白点）的距离 d 做除法，得到商 s/d=100/43.1>θ=0.5 ，因此我们需要执行算法步骤（3）。

对于根节点的第一个子节点，包含的是物体 A 本身，它对本身不施加力，所以我们不做任何事。



对于根节点的（从左到右）第二个子节点，它是一个内部节点，包含节点 B,C,D,E 的总质量和质心。计算得 s/d=50/62.7>θ ，因此我们递归的计算节点第一个非空子树施加给A的力。



这仍然是一个内部节点，它包含有 B,C,D 的总质量和质心。现在 s/d=25/66.9<θ 。于是将这个内部节点视作一个单独的物体，其质量是 B,C,D 的总质量，我们计算它施加在物体A上的力，并将这个值加到A所受的合力上。



接下来我们考虑包含物体E的节点。它是一个叶子节点，因此我们计算A和E之间的作用力，并将其加到A的合力上。



最后我们考虑包含物体F的几点。它是一个叶子节点，因此我们计算A和F之间的作用力，并将其加到A的合力上。

参考文献与推荐阅读材料

【1】 http://arborjs.org/docs/barnes-hut
【2】 http://www.cs.princeton.edu/courses/archive/fall03/cs126/assignments/barnes-hut.html
【3】 Barnes, J. and Hut, P., 1986. A hierarchical O (N log N) force-calculation algorithm. nature, 324(6096), pp.446-449. （百度网盘下载链接）
【4】 牟磊，基于Barnes Hut算法的N-body问题模拟，福建电脑，2010 年第 8 期.（百度网盘下载链接）