决策树（Decision Tree）

决策树（Decision Tree）是一种简单但是广泛使用的分类器。通过训练数据构建决策树，可以高效的对未知的数据进行分类。

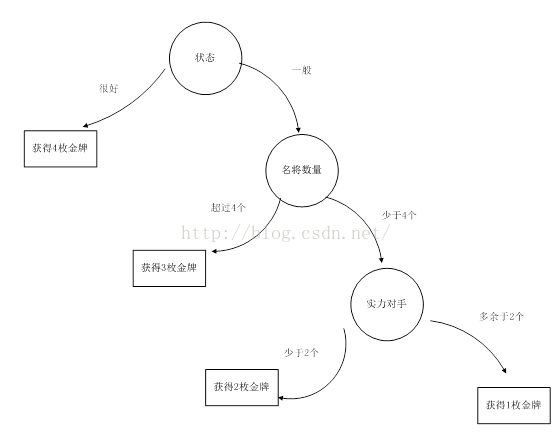
以中国羽毛球队征战里约奥运为例，预测里约奥运会中国羽毛球队能斩获多少枚金牌。

以如下几个因素作为树节点：运动员状态、中国队名将数目，本届奥运会实力对手数进行分割。

算法介绍

决策树进行决策算法有很多，这里介绍一种基于信息增益的算法，就是克劳德.香农提出的熵(entropy),它定义为信息的期望值，信息的含义为：如果待分类的事务可能划分在多个分类之中，则符号的信息定义为：

其中是选择该分类的概率。

而熵的计算就是所有类别可能值包含的信息期望值，通过如下公式得到：

信息增益

基于以上公式原理，可以看下 python 实现的熵计算程序：

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet: 
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1 #统计同类标签的数量
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries #计算同类标签出现的概率值
        shannonEnt -= prob * log(prob,2) #log base 2之和，得到信息熵
    return shannonEnt

基于信息增益的最佳特征值切割

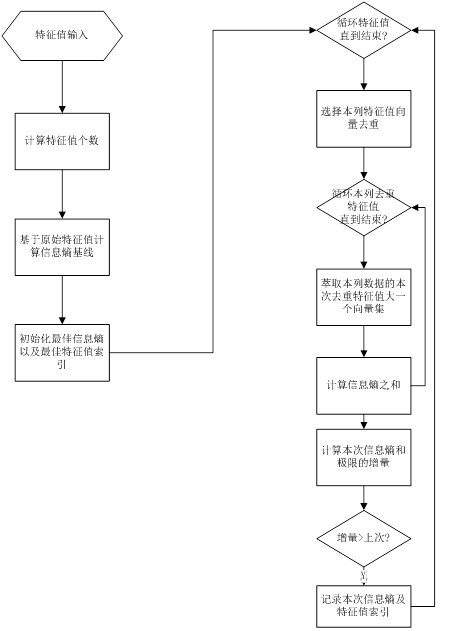
信息熵增益切割是决策树分隔的核心，基本原理是依据信息熵的大小进行特征值索引选择。

流程图如下：

基于特征值循环计算信息熵选择最佳特征值python实现如下：

for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature

决策树创建

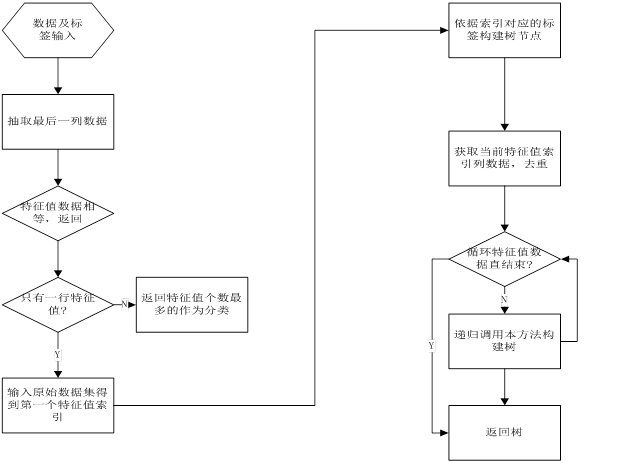
决策树的创建使用递归调用构建，每一层节点的创建是依赖于上一章使用信息熵进行最佳值切割得到。流程图如下：

Python实现代码如下：

bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree

优点

1）决策树模型可以读性好，具有描述性，有助于人工分析；

2）效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

缺点

采用上面算法生成的决策树在事件中往往会导致过滤拟合。也就是该决策树对训练数据可以得到很低的错误率，但是运用到测试数据上却得到非常高的错误率。过渡拟合的原因有以下几点：

噪音数据：训练数据中存在噪音数据，决策树的某些节点有噪音数据作为分割标准，导致决策树无法代表真实数据。

缺少代表性数据：训练数据没有包含所有具有代表性的数据，导致某一类数据无法很好的匹配，这一点可以通过观察混淆矩阵（Confusion Matrix）分析得出。

 

优化方案

优化方案1：修剪枝叶

 

决策树过渡拟合往往是因为太过“茂盛”，也就是节点过多，所以需要裁剪（Prune Tree）枝叶。裁剪枝叶的策略对决策树正确率的影响很大。主要有两种裁剪策略。

 

前置裁剪 在构建决策树的过程时，提前停止。那么，会将切分节点的条件设置的很苛刻，导致决策树很短小。结果就是决策树无法达到最优。实践证明这中策略无法得到较好的结果。

 

后置裁剪 决策树构建好后，然后才开始裁剪。采用两种方法：

1）用单一叶节点代替整个子树，叶节点的分类采用子树中最主要的分类；

2）将一个字数完全替代另外一颗子树。后置裁剪有个问题就是计算效率，有些节点计算后就被裁剪了，导致有点浪费。

 

优化方案2：K-Fold Cross Validation

 

首先计算出整体的决策树T，叶节点个数记作N，设i属于[1,N]。对每个i，使用K-Fold Validataion方法计算决策树，并裁剪到i个节点，计算错误率，最后求出平均错误率。这样可以用具有最小错误率对应的i作为最终决策树的大小，对原始决策树进行裁剪，得到最优决策树。

 

优化方案3：Random Forest

 

RandomForest是用训练数据随机的计算出许多决策树，形成了一个森林。然后用这个森林对未知数据进行预测，选取投票最多的分类。实践证明，此算法的错误率得到了经一步的降低。这种方法背后的原理可以用“三个臭皮匠定一个诸葛亮”这句谚语来概括。一颗树预测正确的概率可能不高，但是集体预测正确的概率却很高。