遗传算法 一个模拟自然进化过程的启发式搜索算法
转载请注明出处:http://blog.csdn.net/smartbetter/article/details/52194663
遗传算法(Genetic Algorithm)是一种模拟自然界“自然选择”和“自然遗传”的启发式搜索算法,通过模拟自然进化过程搜索最优解的方法。
直到1989年,实现了具有单变量函数的简单遗传算法(Simple Genetic Algorithm,SGA)程序,后续有许多学者对遗传算法提出建议或改良,如精英保留策略遗传算法、改良遗传算法、混合遗传算法等,但他们都是基于SGA的。
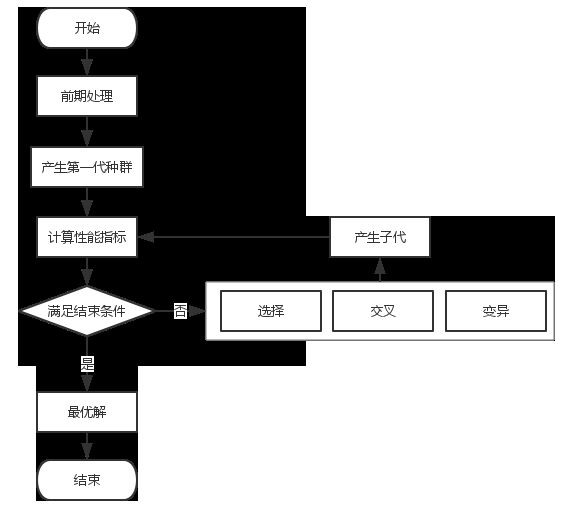
本篇也是以SGA为基础的,SGA处理流程如下:
遗传算法的理论基础是达尔文的“进化论”,在遗传算法模型中,将问题的解答巧妙的编码在一串数值或符号中(即所谓的染色体),模拟染色体中的一段基因,经过长时间的进化过程,历经选择、交叉和变异3个遗传算子,不断产生新基因,同时淘汰不良基因,最终进化成最优秀的染色体,并满足进化的终止条件,得到问题的最优解。
实现遗传算法时,必须先将要求问题解的质量定义为适应度函数。适应度函数计算的数值代表该系统的性能指针,也就是该物种对于生存环境的适应程度,简称为适应度值,适应度值越高,表示系统性能越好,被选取的概率也越大。
最常见的进化的终止条件有两种:得到大于或等于预期的目的适应值,或达到预先定义好的演化代数,也就是说,适应度函数的设计是遗传演算过程是否可以正常执行的关键。
如果适应度函数选择不当,有可能会收敛于局部,而不能达到“真正的全局”最优解。除此之外,由于遗传算法具有不确定的变异因素,可能也会出现无法收敛的情况。这时,可以根据指定的演化函数,或发现搜索结果停滞不前,或已经达到某种饱和现象,设置终止条件。
1.编码
在遗传算法中,将染色体称为个体,常见的基因编码方式有二进制编码、浮点数编码和字符编码3种。
1)二进制编码:用二进制表示参数空间,优点:易实现
2)浮点数编码:直接将参数值当成染色体的基因,省去了编码和译码的动作,缺点:无法默认搜索的精确度,不适合处理不连续的变量空间
3)字符编码:直接用字符代表基因的方式
2.种群
根据SGA处理流程可知,遗传演算开始前,需要先产生初代种群(由一堆随机产生的染色体组成的),由于一个染色体代表一个问题解,因而初代种群也代表初始解的集合。
那一个种群应该包括多少染色体呢?这个要视问题复杂度来定,一般来说,越复杂的问题需要越大的种群规模来解决。
3.选择
选择机制类似于“无性繁殖”,根据每个染色体的适应度值大小来决定该染色体被选择的概率,适应度越高,被选择概率就大(自然选择),一旦染色体被选择,就会进行“自我复制”,并且被放置在称为配对库的暂存区中。
实现选择机制的两种常用方法是竞争选择法和轮盘赌选择法。
1)竞争选择法
从种群中选出两个染色体进行适应度值的比较,最后留下适应度较高的染色体作为父代,重复进行这个步骤,直到选出所有的父代为止。
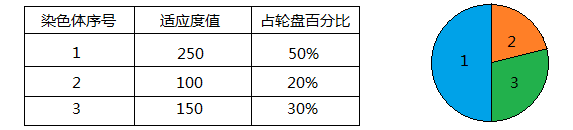
2)轮盘赌选择法
按照适应度值的大小决定每一个槽的面积大小,可以使用下面公式来表示:
被选中的概率 P(i)= f(i)/( f(1) + f(2) + … + f(S))
其中 f(i):适应度值;S:染色体总个数;
也就是说个体被选中的概率与其适应度函数值成正比。
接下来我们来看一个简单的轮盘赌算法:
/** * 按设定的概率随机选中一个染色体,P(i)表示第i个染色体被选中的概率 */
int RAN() {
m =0;
r =Random(0,1); // r为0至1的随机数
for(i=1;i<=S; i++) {
/** * 产生的随机数在m~m+P[i]间则认为选中了i,i被选中的概率是P[i] */
m = m + P[i];
if(r<=m) return i;
}
}4.交叉
第二个遗传算子叫做交叉。
作用:希望通过父代之间进行基因交换的动作后,产生具有较高适应度的子代。
位于配对库中的染色体是经过选择运算的结果,在交叉流程开始时,会先从配对库中任意取出两个染色体,并将它们作为父代。但是并非所有父代都会进行交叉(取决于交叉概率),实现程序时,可以将交叉概率设置为0.8~1的数值,接着再取一个随机实数,如果该随机实数小于交叉概率,就进行交叉运算。
交叉概率的大小会影响搜索最优解的速度,太高的交叉概率有可能流失优良的染色体,反之又会造成进化停滞,故一般把交叉概率设置在0.8~1为宜。
5.变异
最后一个遗传算子叫做变异。
是否进行变异取决于变异概率,当随机实数小于变异概率时就会引发突变运算,也就是会将染色体中的某个位,由原来的0置换成1,或是由原来的1置换成0。可以置换某个固定位置的位,也可以由随机数来决定位置。
使用这种随机漫步的方式,突变运算将使遗传算法脱离布局最优解的窘境,得到全局最优解。根据文献研究显示,建议将变异概率设置为0.001左右。
6.演化迭代
经过选择、交叉、变异3个遗传算子后,即可产生新的子代,继续下一个循环的进化,目前常用的取代方式有:
1)整群取代:全部用新产生的染色体取代旧种群的染色体;
2)精英保留策略:保留旧种群中适应度值最高的前几名,用新产生的染色体取代其余的染色体。
7.基本遗传算法伪代码
/** * 基本遗传算法伪代码 * Pj:交叉发生的概率 * Pb:变异发生的概率 * M:种群规模 * G:终止进化的代数 * T:进化产生的任何一个个体的适应度函数超过T,则可以终止进化过程 */
初始化Pb,Pj,M,G,T等参数,随机产生第一代种群Pop
do{
计算种群Pop中每一个体的适应度f(i),初始化空种群newPop
do{
根据适应度以 轮盘赌算法 从种群Pop中选出2个个体
if ( random ( 0 , 1 ) < Pj ){
对2个个体按交叉概率Pj执行交叉操作
}
if ( random ( 0 , 1 ) < Pb ){
对2个个体按变异概率Pb执行变异操作
}
将2个新个体加入种群newPop中
} until ( M个子代被创建 )
用newPop取代Pop
} until ( 任何染色体得分超过T, 或繁殖代数超过G )到这里相信大家对遗传算法已经有了一定的了解了。