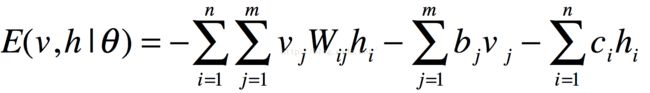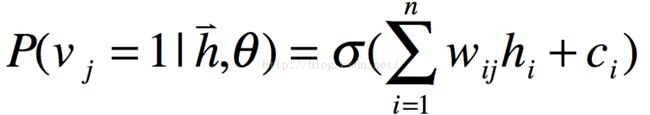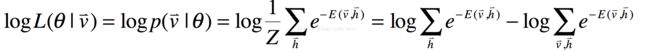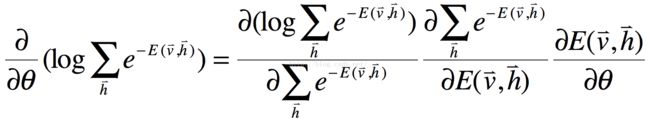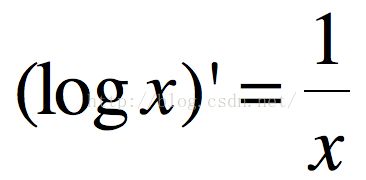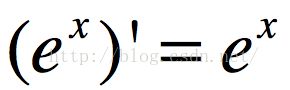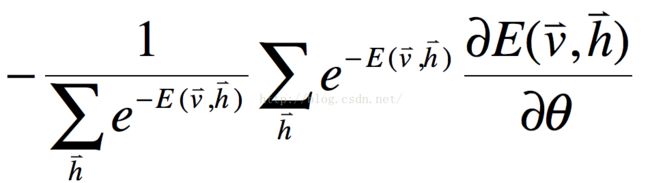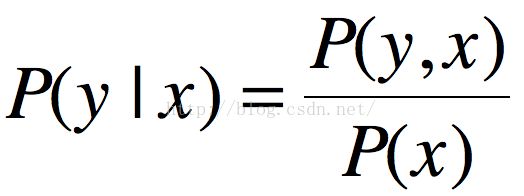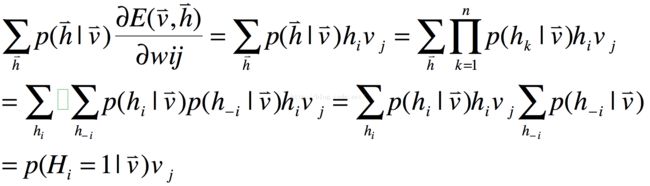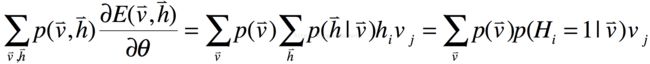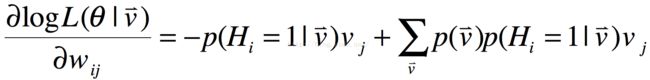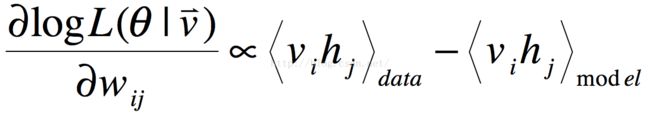深度学习算法实践16---限制性波尔兹曼机(RBM)原理1
我们目前的讨论的神经网络,虽然学习算法不同,但基本上架构还是相同的,就是都是分层网络,即神经元按层进行组织,层内神经元无连接,层间神经元间有连接。我们在这篇博文中,将讨论一种非常不同的神经网络,这类神经网络是由没层次关系的神经元全连接网络进化而来,采用有别于梯度下降算法进行学习的网络。
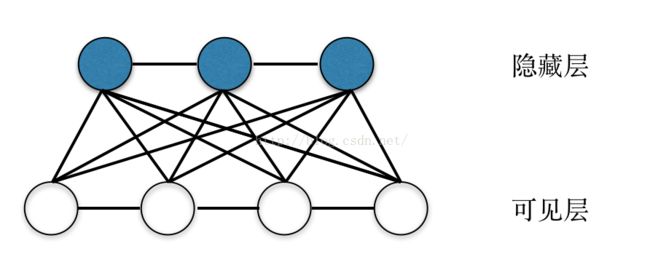
这类网络首先起源于Holpfield网络,这是一种全联接的网络,神经元之间进行全连接,我们可以给这个网络定义一个能量函数,神经网络的学习任务就是使能量函数达到最小值。这类网络典型的成功应用是担货郞问题,即有N个地点,每个地点间都有道路相通,担货郞必须把货物送到每个地点,通过Holpfield网络,可以有效地找到最佳路径。但是即使是对于二值(神经元只能处在0或1状态),全联接网络的状态也2的N次方个状态,要从这些状态中找到找到能量函数的最小值,难度相当大,大家一定还记得国际象棋发明者,向国王讨赏的典故吧,一个64个方格的棋盘,连全世界总粮食产量都填不满,可见这个问题的复杂性。与此同时,根植于统计力学模型的波尔兹曼机(BM)也开始流行起来。在这种网络中,神经元的输出只有激活和未激活两种状态,用0或1来表示,各个神经元的输出值由概率纺计模型给出。典型的波尔兹曼机(BM)的网络模型如下图所示:
由实践来看,波尔兹曼机(BM)具有强大的非监督学习能力,可以发现数据中潜在规则,理论上来讲,非常适合于数据挖掘领域应用。便是由于是全连接网络,导致这种网络的训练时间非常长,没有高效的学习算法,直接制约了这种网络的应用。
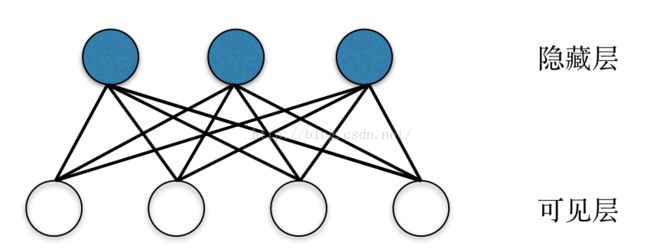
后来Smolensky引入了限制性波尔兹曼机(RBM)模型,其主要思想就是去掉了波尔兹曼机中层内连接。限制性波尔兹曼机(RBM)具有一个可见层,一个隐藏层,层内神经元间无连接,层间神经元全连接,如下图所示:
限制性波尔兹曼机(RBM)中,输入信号通过可见层输入到网络中,此时传播到隐藏层后,各隐藏层神经元的激活是互相独立的,同理在给定隐藏层信号后,反向传播到可见层时,可见层神经元的激活也具有独立性。可以从理论上证明,这种网络结构,只要隐藏层神经元节点足够多,限制性波尔兹曼机(RBM)可以拟合任意离散分布。虽然在理论上RBM很好,但是一直由于没有高效的学习算法,限制性波尔兹曼机(RBM)并没有得到广泛应用。但是深度学习之父Hinton在2002年提出了对比散度(CD)算法,使限制性波尔兹曼机(RBM)具备了快速学习的能力。从此,RBM得到了广泛的应用,出现了各种对比散度算法的变种,使得算法收敛性更高。与此同时,波尔兹曼机(RBM)在分类、回归、降噪、高维时间序列分析、图像特征提取、协同过滤等方面,得到了广泛的应用,在年初Science子刊上发表了利用限制性波尔兹曼机(RBM)分析非结构化病例信息,从其中进行医学诊断知识,并成功应用于癌症早期筛查,表明RBM在非结构化数据处理方面,也有实用价值。另外,Hinton在2006年提出,将限制性波尔兹曼机(RBM)堆叠起来,形成深度信念网络(DBN),通过逐层训练RBM网络,将训练好的RBM网络堆叠成深度学习网络,可以得到非常好的初始参数值,有效地解决了大型神经网络训练速度慢的问题,是当前的研究热点之一。
在介绍了这么多限制性波尔兹曼机(RBM)的基本情况之后,下面我们来具体介绍一下RBM的理论基础。
如上图所示,RBM的可见层用v表示,用于接收输入信号,隐藏层由h表示,可以视为是输入信号的特征提取器。我们在前面讨论过,制约神经网络大规模应用的一个瓶颈之一,就是很难为研究问题找到合适的特征,而RBM则是通过无监督学习方式,自动找到研究问题的最佳特征,因此对于研究者们而言,具有非常大的吸引力,这也是为什么RBM在近些年来如此火的原因。我们设定可见层神经元为二值变量,即,隐藏层单元同样为二值变量,即
,假定可见层有m个神经元,用下标i代表第j个神经元,隐藏层有n个神经元,用下标j表示第j个神经元。
我们可以定义网络的能量函数为:
上式中为网络参数,均为实数,Wij为可见层神经元i到隐藏层神经元j的连接权值,bj为可见层第j个神经元的偏置,ci为隐藏层第i个神经元的偏置。
接下来我们定义关于可见层和隐藏层的联合概率分布:
式2
Z为归一化因子,其定义为:
式3
熟悉机器学习算法的都知道,我们需要知道的实际上是输入样本的概率分布,也就是式2的P的边际分布,也称为似然函数,定义如下所示:
式4
因为需要计算归一化因子,而这需要
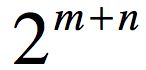 次运算,对于高维问题,即使我们可以通过算法得出网络的参数,但是由于运算量过大,这个公式在实际应用过程中,也不能直接应用。
次运算,对于高维问题,即使我们可以通过算法得出网络的参数,但是由于运算量过大,这个公式在实际应用过程中,也不能直接应用。
但是,由于限制性波尔兹曼机(RBM)具有层间全连接,层内无连接,当我们将输入信号输入到可见层时,可见层将决定隐藏层各神经元的状态,而且由层内无连接,此时隐藏层神经元的激活状态是条件独立的,隐藏层第j个神经元激活状态的概率为:
式5
与此同理,如果隐藏层状态完全确定时,可见层第i个神经元激活状态也是条件独立的,其公式为:
对于RBM学习算法,我们会用到对数似然函数,其定义如下所示:
在式7的推导中,我们代入了式4的内容,同时把对数内除法转化为了对数的减法。
我们需要的是对数似然函数对于参数的导数,如下所示:
式8
由于式8比较复杂,我们需要分别对第一项和第二项进行求导,考虑到大家对数学公式的熟悉程度,我们将一步一步进行推导,中间用到的数学公式,我们会在文中列出。
对于式8的第一项来说,我们首先需要应用链式求导法则,如下所示:
我们在高数中,常用函数的求导公式可知:
指数函数求导公式:
将式10和式11代入式9,可以得到如下结果:
在这时我们要注意,我们不能将第一项和第二项消去,而是应该将第一项视为一个常数,将其代入第二项的叠加符号内。
根据隐藏层在可见层条件下的概率密度函数定义,我们可以得到如下结果:
式13
在这个推导中会用到概率论中的贝叶斯公式,即条件概率定义:
将式13代入式12,可以得到如下结果:
式15
到此为止,我们成功求出了式8的第一项,下面我们还是应用链式求导法则,来化简式8的第二项,结果如下所示:
式16
推导方法与第一项类似,只不过在推导过程中,用到了式3和式4的定义。因此对数似然函数对参数的求导公式最后可以化简为如下形式:
式17
对于限制性波尔兹曼机(RBM)而言,参数是权值矩阵W、可见层偏置c,隐藏层偏置b,下面我们根据式17分别求对于他们的导数,我们首先来求对权值的导数,如下所示:
式18
由于式18比较复杂,下面我们分别对第一项和第二项进行求解,对于第一项,我们根据能量函数E的定义(式1),其对wij求导的结果为hivj,结果如下所示:
接着我们来求式18的第二项:
因此式18的最终结果为:
如果我们采取在线学习模式,即每个训练样本均更新神经网络的参数,式21即可作为权值调整值来使用,但是由于样本的随机性,这样的参数调整效率会比较低,因此实际中使用更多的是迷你手批量学习模式。假设设置批量学习样本为:
式22
则式21的导数可以表示为该批次内对所有训练样本求导的平均值,如下所示:
式22
式22中,q代表经验分布,通常我们有如下结果:
与求导对数似然函数对权值的导数方法类似,我们同样可以求出对可见层偏移量bj的导数,最后结果为:
式24
同理对数似然函数对隐藏层偏移量ci求导数的结果为:
式25
式21、式24、式25中的第二项,可以通过Gibbs采样得到,但是这需要运行受限波尔兹曼机(RBM)很长时间,即可见层到隐藏层,再从隐藏层到可见层,反复运行,最后达到静止点,这就是马可夫链蒙特卡罗方法。但是这种方法运算量非常大,在2006年以前,受限于此,RBM很少应用在实际问题中。在2006年,深度学习之父Hinton提出了CD-k算法,而且通常k=1,可以很好的解决定一问题,才使RBM具有了应用价值,并且直接促使深度信念网络(DBN)的广泛使用。
受限波尔兹曼机(RBM)算法推导过程就基本讲完了,在下一篇博文中,我们将介绍一下CD-k算法。