特征选择之信息增益法

设计分类系统的时候，一个很重要的环节便是特征选择，面对成千上万上百万的特征，如何选取有利于分类的特征呢？信息增益(Information Gain)法就是其中一种简单高效的做法。本文首先介绍理解信息增益(Information Gain)需要的基本概念，之后介绍如何将其运用在特征选择中，最后以stanford-nlp中利用信息增益法实现特征选择的例子结束本文。

熵(Entropy)

介绍信息增益大法前，不得不提的一个概念就是熵。熵是信息论中一个很重要的概念，我们先看看它的长相：

H(X)=−∑xp(x)logp(x)

不得不承认，熵长得挺恶心的，从表达式中完全看不出半点端倪，根本不知道它有何作用。别急，我们慢慢研究，希望最后可以得到一个直观理解。

如何量化信息

平时我们会这样说”这句话信息量好大”，我们通常所指的信息是指那句话里的语义，而这里我们谈的信息则是信息论鼻祖Shannon定义的，Shannon老爷子认为消息传递的过程是这样的：消息首先被编码器编码之后经过一定的通道再经过解码器解码，最后信息传递给目标。那么目标者能获得多少原来的信息则是我们这里所谈的信息，这样的信息可能是一堆废话，完全没”信息量”。
我们知道信息在传递的时候有很多不确定因素，而量化不确定因素的一个利器就是概率论，那么在概率框架下的信息的定义是这样的：对于一个事件 i ，它发生的概率是 pi ，那么当观察到该事件的时候，我们到底获得多少信息呢？Shannon老爷子是这样定义信息函数的：

I(p)=−log(p)

,并规定底可以取大于1的任意数，通常可以取 2,e,10 等。为什么要以对数来定义呢？在老爷子自己的开山大作 《A Mathematical Theory of Communication》中给了三个理由：

第一，这样定义在实际中非常有用(不管黑猫白猫理论)，工程的重要参数随数据概率的对数而线性改变。如时间、带宽、继电器数，等等。
第二，对数更接近我们本身的直观感受，我们是线性直观地测量实体对象，例如两张穿孔卡片比一张具有有两倍信息贮存量。
第三，以对数定义信息在数学上可以得到极大便利。

信息函数的性质

我们参考一下维基百科看看这样定义的性质有什么：

I(p)>=0......(1)I(1)=0......(2)I(p1,p2)=I(p1)+I(p2)......(3)

(1)式讲的是信息是非负的，我们最坏情况是得不到信息。(2)式表面必然发生的事情是不含信息量的，如果我们被告知地球是球状的，我们不会获得什么直接信息吧(除了觉得那个人有毛病)。(3)式则是说对于两个独立事件发生产生的信息量等于我们各自观察每个事件所获得的信息量。看，这样定义信息其实也挺符合我们对信息的通常理解。
那么回过头来看看我们的老朋友熵：

H(X)=−∑xp(x)logp(x)=∑xp(x)I(x)

那么熵可以看成是观察事件 X 发生后我们获得的期望信息量，如果 H(x) 越大，那么说明我们获得的信息量越大，同时也说明 X 更趋向于均匀分布，由上面(2)式可知，信息量大不大反应于我们对事件发生可预知的概率大不大，如果我们知道事件肯定发生或者肯定不发生，我们得到的信息量是0，而越是对事件越不确定，越能够从这样的事件获得信息。那么当事件发生的概率是0.5的时候，我们获得最大的熵。再看一个常见的例子，假如我们在抛一枚硬币的事件是 X ，我们看看 H(X) 与看到正面的事件的概率 Pr(X=1) 所构成的图像是怎样的：

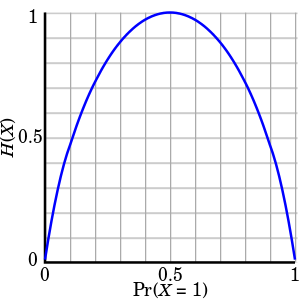
从图像中我们可以知道，当 Pr(X=1)=0.5 的时候， H(X) 达到峰值。因此我们可以这样直观地理解熵：熵是用来衡量事件可预知性，熵越大，事件发生的概率越随机。

条件熵(Conditional Entropy)

我们的目的是特征选择，那么现在假设我们在做一个垃圾分类器，首先我们从训练数据 X={x1,x2,...,xn} 中抽取特征，将每个输入 xi 映射到特征空间 Fi={f1,f2,...,fm} ，然后通过我们熟悉的机器学习算法比如SVM,NaiveBayes,LogisticRegression等等，从训练数据中获得这样的模型：

f(F)=C

C=1 代表输入是垃圾， C=0 代表是输入非垃圾。很不幸，通常 m 将会很大，几万或几百万，这样不仅导致冗长的训练时间，甚至导致严重的Overfitting。那么我们便希望通过某种方法，将 m 变小，降低到几千或者几百。接下来进入我们的尝试阶段。

定义

我们先来看看这小节的主角的形象：

H(X|Z)=−∑zp(z)∑xp(x|z)log(p(x|z))=−∑x∑zp(z)p(x|z)log(p(x|z))=−∑x∑zp(x,z)logp(x,z)p(z)=∑x∑zp(x,z)logp(z)p(x,z)

性质

好吧，看容貌，条件熵更加平易远人，我们知道熵是非负的，那么上面那一坨定义是否也是非负呢？利用Jensen不等式我们可以检验：

H(X|Z)=∑x∑zp(x,z)logp(z)p(x,z)≥log∑x∑zp(x,z)p(z)p(x,z)=log∑zp(z)=0

那么我们的定义应该没有问题。我们再来看看它和单独的 H(X) 有什么关系，我们可以检验一下 H(X)−H(X|Z) 的正负性，经过类似上面的推导，我们知道：

H(X)≥H(X|Z)

也就是 H(X) 是 H(X|Z) 的上界(upbound)。

现在先不管复杂的表达式，我们试之从直觉上理解。上一节我们了解到熵是衡量事件发生的可预知性，那么条件熵我们可以这样理解，事件 Z 发生了对于我们知道事件 X 有什么贡献。当事件 Z 发生了但是完全没贡献时候，当前仅当 H(X)=H(X|Z) ，此时事件 X 与事件 Z 相互独立，否则，只要 H(X|Z)≥0 ，事件 Z 就对我们预知事件 X 有贡献，因为 H(X|Z)≤H(X) 的， Z 的出现导致熵变小了，我们对事件 X 的预知能力变强了。

尝试利用条件熵做特征选择

那么对于分类器而言，我们想知道某个特征对于分类这样的事件到底有多大贡献，然后对贡献太小的特征就舍弃，从而达到特征选择地效果。现在我们就进行尝试，假设我们有一个事件 F ， f1＝1 代表在我们拥有 f2,f3,...,fm 的情况下，再包含特征 f1 的事件， f1=0 则表明不包含特征 f1 的事件。那么我们想知道 f1,f2 对于我们识别垃圾到底哪个贡献大，我们可以比较 H(C=1|f1),H(C=1|f2) 看看哪个更小，熵小的特征说明对于识别信息为垃圾的事件贡献更大。于是我们计算所有特征都的 H(C=1|fi) ，按照从小到大排序，取前 K 个特征，太棒了，貌似我们解决了特征选择问题了。但是我们再仔细思考一下，上面的做法只是筛选出了对于识别是垃圾这种类别有用的特征，但是可能刷掉了对于识别非垃圾事件有用的特征，怎么办呢？我们可不可以比较一下 H(C=1|f1)，H(C=0|f1) 的大小从而决定该特征是对识别为垃圾的事件贡献大还是对识别为非垃圾的贡献大呢？答案是否定的，因为两者不具备可比性，为什么呢？因为两者具有不同的上界，不在同一标准，所以不具备可比性。那该怎么办呢？

信息增益(Information Gain)

上一节我们一开始以为找到了特征选择的办法，后来发现是不可行的，这一次，我们的主角将为我们解决难题。

定义

老套路，我们还是先看看老兄的形象：

IG(X,Z)=H(X)−H(X|Z)=H(Z)−H(Z|X)

有了前两节的基础，老兄并不那么面目可憎，反而有点熟悉，似曾相识。没错，你没有认错，上一节中我们为了证明 H(X) 是 H(X|Z) 上界，就已经出现上述所示。这次我们并不是要证明什么上界下界，我们直接对其差值进行定义，并取名字为信息增益(Information Gain)。

性质

我们照常来看看信息增益的一些性质。首先从定义可以很容易知道它符合交换律，也就是

IG(X,Z)=IG(Z,X)

，其次信息增益具有非负性

IG(X,Z)≥0

当且仅当 X,Z 相互独立的时候等号取得成立。我们可以这样直观地理解信息增益的含义：观察到事件 Z 对于我们预知 X 提供了多少信息，或者观察到事件 X 对于我们预知 Z 提供了多少信息。通过定义我们可以很容易验证两种描述都是正确的。因此我们称之为信息增益，观察到一个事件，另一个事件获得了多少信息。我们类比一下高中学过的重力势能，不同高度的重力势能是不同的，但是对于相同的高度差，重力势能的差值却是相同的。
由于两个事件相互的信息增益是相同的，所以信息增益也叫相互信息(Mutual Information)。对于定义，我们可以展开重写一下：

IG(X,Z)=H(X)−H(X|Z)=−∑xp(x)logp(x)+∑z∑xp(x,z)logp(x,z)p(z)=−∑x∑zp(x,z)logp(x)+∑z∑xp(x,z)logp(x,z)p(z)=∑z∑xp(x,z)logp(x,z)p(z)p(x)=KL(p(x,z)||p(x)p(z))

突然出现一个新人物，Kullback-Leibler Divergence，对于 KL(p||q) ，可以近似认为他是衡量分布p与q的距离，当两个分布相同的时候，KL散度为0，越是不同，KL散度越大。所以信息增益又被称为Information Divergence。我们可以理解为它是衡量联合分布 p(x,z) 与假设他们 X,Z 相互独立时的联合分布 p(x)p(z) 之间的散度。

利用信息增益做特征选择

上一节中，我们说过 H(C=1|f1),H(C=0|f2) 不具备可比性，因为他们具有不同的上界 H(C=1),H(C=0) ，从而阻止我们利用条件熵来做特征选择，这次我们利用信息增益再看看会不会有相同问题。我们看

IG(C=1,f1)与IG(C=0,f1)

是否具有可比性，由于两者都是算当包含或不包含特征 f1 的时候，为识别为垃圾的事件带来多少信息，为识别为非垃圾带来多少信息，那么我们可以直接用

IG(C,f1)

来衡量特征当包含或不包含 f1 的时候，为分类器的识别提供了多少信息量，同理可以利用

IG(C,f2)

来衡量包含或不包含特征 f2 为分类器提供了多少信息量，依次类推，我们分别求出每个特征对分类器提供的信息量，然后从大到小进行排序，取前 K 个特征，我们就达到利用信息增益做特征选择的目的！

信息增益法在stanford-nlp的应用

前面讲了那么多理论，该是大显身手的时候了。我们再回过头来看如何求取分类与特征之间的信息增益。首先观察定义：

IG(C,fi)=H(C)−H(C|fi)=−∑c∈{0,1}p(c)logp(c)+∑fi∈{0,1}p(fi)∑c∈{0,1}p(c|fi)logp(c|fi)

，我们知道计算信息增益分为两部分，一部分是计算类别 C 的熵 H(C) ，另一部分是计算在事件 fi 下的条件熵 H(C|fi) ，计算熵的时候，涉及到概率计算，我们通常都是采用极大似然法来估计概率，各个概率的估计如下：

假设我们的训练样本数是 N

p(C=0)=count(c=0)Np(C=1)=1−p(C=0)

对于 p(fi)和p(c|fi) 的估计，stanford-nlp中首先是对每个训练样本进行统计，对于每个特征 fi 在训练样本 x 中只要出现过就加一次，出现两次也算一次。这样计数下来就可以统计到每个特征的featureCount。那么接下来的估计如下：

p(fi=1)=count(fi=1)Np(fi=0)=1−p(fi)p(C=0|fi=1)=count(C=0,fi=1)count(fi=1)p(C=1|fi=1)=count(C=1,fi=1)count(fi=1)p(C=0|fi=0)=count(C=0,fi=0)count(fi=0)p(C=1|fi=0)=count(C=1,fi=0)count(fi=0)

且看Dataset里面的一段代码：

  public double[] getInformationGains() {
    labels = trimToSize(labels);
    ClassicCounter<F> featureCounter = new ClassicCounter<F>();
    ClassicCounter<L> labelCounter = new ClassicCounter<L>();
    TwoDimensionalCounter<F,L> condCounter = new TwoDimensionalCounter<F,L>();
    for (int i = 0; i < labels.length; i++) {
      labelCounter.incrementCount(labelIndex.get(labels[i]));
      boolean[] doc = new boolean[featureIndex.size()];
      for (int j = 0; j < data[i].length; j++) {
        doc[data[i][j]] = true;//标识一下特征是否出现过
      }
      for (int j = 0; j < doc.length; j++) {
        if (doc[j]) {//统计count(fi)和count(c|fi)
          featureCounter.incrementCount(featureIndex.get(j));
          condCounter.incrementCount(featureIndex.get(j), labelIndex.get(labels[i]), 1.0);
        }
      }
    }

    double entropy = 0.0;//计算H(C)
    for (int i = 0; i < labelIndex.size(); i++) {
      double labelCount = labelCounter.getCount(labelIndex.get(i));
      double p = labelCount / size();
      entropy -= p * (Math.log(p) / Math.log(2));
    }

    double[] ig = new double[featureIndex.size()];
    Arrays.fill(ig, entropy);
    //计算H(C|fi)
    for (int i = 0; i < featureIndex.size(); i++) {
      F feature = featureIndex.get(i);
      double featureCount = featureCounter.getCount(feature);//count(fi=1)
      double notFeatureCount = size() - featureCount;//count(fi=0)
      double pFeature =  featureCount / size();//p(fi=1)
      double pNotFeature = (1.0 - pFeature);//p(fi=0)
      if (featureCount == 0) { ig[i] = 0; continue; }
      if (notFeatureCount == 0) { ig[i] = 0; continue; }
      double sumFeature = 0.0;
      double sumNotFeature = 0.0;
      for (int j = 0; j < labelIndex.size(); j++) {
        L label = labelIndex.get(j);
        double featureLabelCount = condCounter.getCount(feature, label);//count(c,fi=1)
        double notFeatureLabelCount = size() - featureLabelCount;//count(c,fi=0)
        double p = featureLabelCount / featureCount;//p(c|fi=1)
        double pNot = notFeatureLabelCount / notFeatureCount;//p(c|fi=0)
        if (featureLabelCount != 0) {
          sumFeature += p * (Math.log(p) / Math.log(2));
        }
        if (notFeatureLabelCount != 0) {
          sumNotFeature += pNot * (Math.log(pNot) / Math.log(2));
        }
      }
    ig[i] += pFeature*sumFeature + pNotFeature*sumNotFeature;//最后H(C)+H(C|F)
         return ig;
  }

对于每个特征计算信息增益后，进行排序，然后就可以愉快地取前 K 个特征了！

参考文献

维基百科Entropy: https://en.wikipedia.org/wiki/Entropy_(information_theory)
课程Text Mining and Analytics第一周最后4节:https://class.coursera.org/textanalytics-001/lecture