一文读懂KMP算法

KMP算法用来解决什么问题

KMP算法是由D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的，因此该算法以三位作者的名字缩写而成
KMP用来解决的问题是：给定一个由n个字符构成的文本，一个由m（m<=n）个字符构成的字串，从文本中寻找给定子串，如果子串存在，则返回文本中第一个匹配子串最左元素的下标，否则返回-1

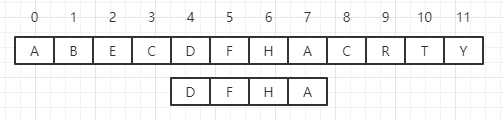
上图中的字符串匹配结果将返回4

字符串匹配的暴力解法

字符串匹配的暴力解法的思想是很简单的，将字串对准文本的前
m个字符，然后从左向右依次匹配对应字符，直到m个字符全部匹配成功；否则，将文本向右移动一位，字符换从头开始，继续匹配，以此类推，直到算法结束

暴力匹配的程序如下

public class SubStr {
    public static int getIndexOf(String str1, String str2) {
        int n = str1.length();
        int m = str2.length();
        for (int i = 0; i <= n - m; i++) {
            int j = 0;
            while (j < m && str1.charAt(j + i) == str2.charAt(j)) {
                j++;
                if (j == m)
                    return i;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        String str1 = "abcab124agf";
        String str2 = "124agf";
        System.out.println(SubStr.getIndexOf(str1, str2));
        System.out.println(str1.indexOf(str2));
    }
}

暴力匹配的算法时间复杂度为$O(mn)$

暴力算法存在的问题

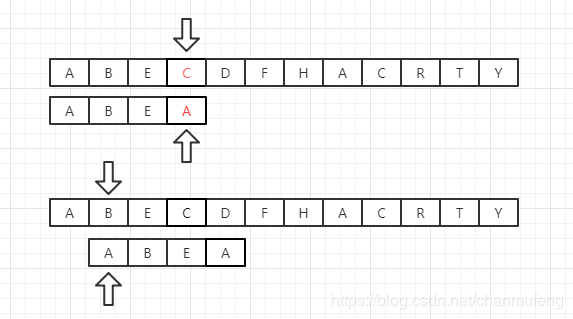
暴力算法虽然写起来优雅简单，但是时间复杂度太高，因为每次文本只会向前推进一个字符，试想下面的情况：

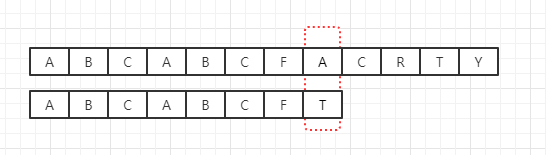
此时A和T不匹配，按照暴力匹配的想法应该是如下变换

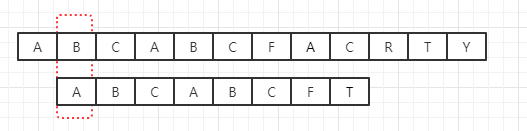
但事实上，我们已经知道了文本中已经有一部分是“ABCABC”，并且字串有一部分也是“ABCABC”，因此进行下一步匹配时，最佳的变换策略应该如下：

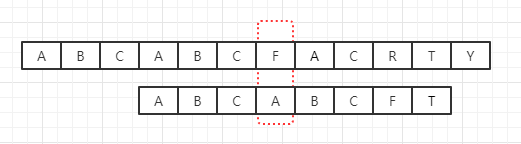
如此一来，我们就能利用已知的匹配信息，扩大文本的移动步长，而不再是逐个字符进行移动，这也是KMP算法的精髓

接下来介绍KMP算法

KMP算法

前缀与后缀的最长公共长度

在学习KMP之前，首先需要了解一个概念：最长前缀与后缀
我们直接通过例子来讲解概念，给定字符串如下

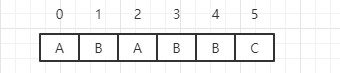
需要注意一点的是：前缀不包含最后一个字符，后缀不包含第一个字符（原因下文说明）

对下标为2的A而言：

• 前缀有：A、AB
  （因为B对于下标为2的A而言就是最后一个字符）
• 后缀有：B、AB （因为坐标为0的A是第一个字符）
  所以对于下标为2的A而言，前缀与后缀的最长公共长度为0，因为A和B不相等

对下标为3的B而言：

• 前缀有：A、AB、ABA
  （因为A对于下标为3的B而言就是最后一个字符）
• 后缀有：A、BA、ABA （因为坐标为0的A是第一个字符）
  所以对于下标为3的B而言，前缀与后缀的最长公共长度为1，因为前缀A和后缀A相等

在此，我们说明一下为什么前缀不包含最后一个字符，后缀不包含第一个字符。
因为我们当前操作的目的是获取某个字符的所有前缀和后缀中的最长公共字符串的长度
如果前缀可以包含最后一个字符，后缀可以包含第一个字符,那么显然前缀与后缀的最长公共长度为当前字符的下表值，这是完全没有意义的！！

我们最后再举一个例子
对下标为4的B而言：

• 前缀有：A、AB、ABA、ABAB
  （因为B对于下标为4的B而言就是最后一个字符）
• 后缀有：B、AB、A、BAB、ABAB （因为坐标为0的A是第一个字符）
  所以对于下标为4的B而言，前缀与后缀的最长公共长度为2，因为前缀AB和后缀AB相等，长度为2

特别地，我们指定下标为0的字符对应的前缀与后缀的最长公共长度为-1
下标为1的字符对应的前缀与后缀的最长公共长度为0

因此，我们可以得到给定字符串的一个数组

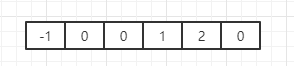
这个数组表示的即为对应字符的前缀与后缀的最长公共长度，这里我们称这个数组为nexts数组
比如，下标为5的C对应的前缀与后缀的最长公共长度为0

搞清楚nexts数组的含义之后，我们假设已经有了某个算法能够求出某个字符串的nexts数组（具体的求解方法会在后文解释，这里我们先使用nexts数组即可），我们来讲解nexts数组是如何加快字符串匹配的

nexts数组在KMP中的使用

分为以下三种情况

1. 当文本字符和子串字符对应相等
   
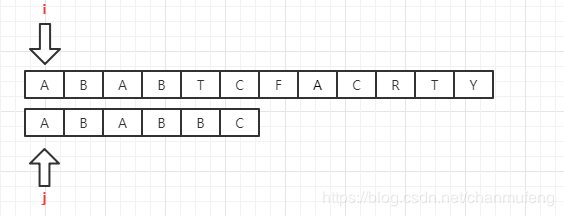
   只需要将文本的指针i和字串的指针j分别增1即可，即i++,j++,然后继续比较
2. 字串的第一个字符就和文本不匹配
   此时只需要将文本的指针向右移动一个字符即可，字串的指针仍然停留在下标为0的位置，即i++
   
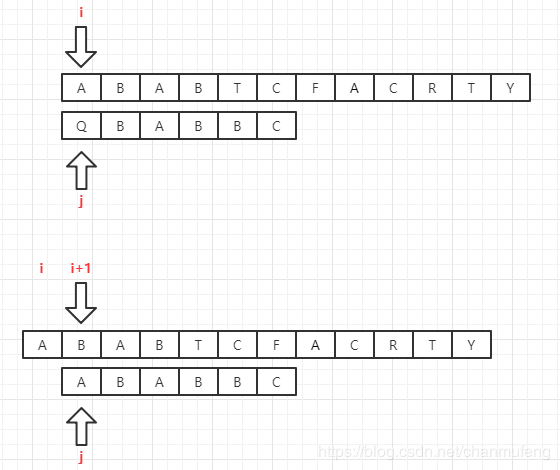
3. 以上两种条件都不符合时
   即子串的某个字符和文本的对应位置字符匹配失败，并且该字符不是子串的第一个字符
   

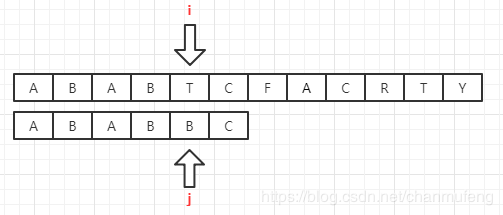
此时，j=nexts[j],nexts就是上文我们求得的“ABABBC”的前缀与后缀的最长公共长度数组。表示的含义为：将子串的指针变换为当前指针所指向的nexts数组的值的位置，再来回忆一下之前求得的nexts数组

当前j指向的字符B对应的nexts数组的值为2，因此，将j指向子串的下标为2的位置，继续向后比较。
如下图所示

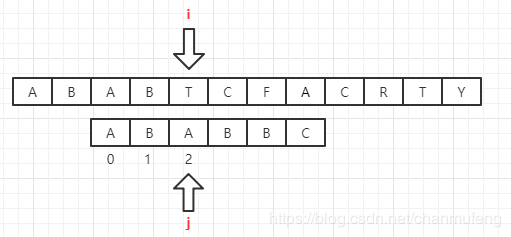
接下来我们来说明，KMP为什么可以直接跳过某些字符，加快搜索
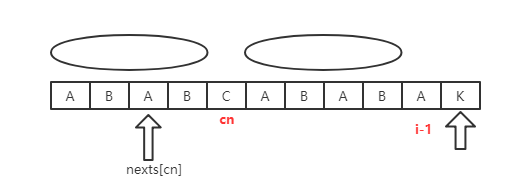
如下图所示，假设X和Y字符之前的所有字符都匹配成功，且Y的最长前缀和最长后缀表示范围如椭圆所示

根据KMP算法，接下来子串将会按照Y的nexts中的值改变当前指针，如下图所示

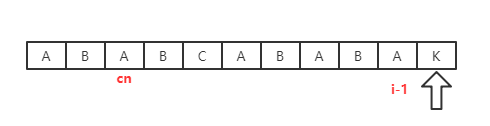
那么问题来了，为什么i和k之间的位置不需要作为匹配的位置，而是直接跳过了呢？？我们这里用反证法来证明，假设i和k之间的位置p处可以进行匹配，则会出现如下情况

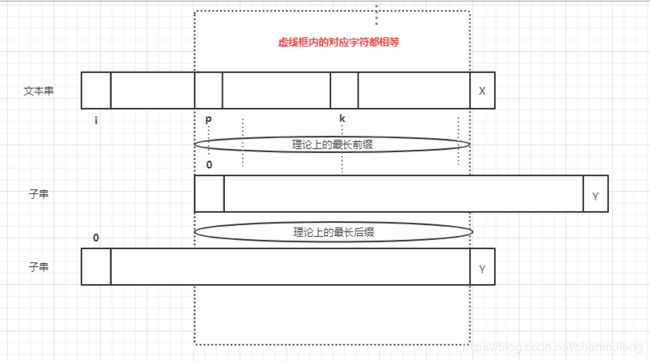
而实际上，字符Y对应的nexts数值并没有我们推导出来的“理论上的最长前缀”那么长（仅从图像宽度就可以看出来），所以矛盾，因此j=nexts[j]的合理性得到证明

到此为止，KMP算法的核心已经介绍完了，理解了上面的内容，代码也就很容易了

/**
 1. 判断str2是否在str1中，是则返回起始字符索引在str1中的索引，否则返回-1
 */
public class KMP {
    public static int getIndexOf(String str1, String str2) {
        if (str1 == null || str2 == null || str2.length() < 1 || str1.length() < str2.length()) {
            return -1;
        }
        int i = 0;
        int j = 0;
        // getNext方法将在下文介绍，这里提前使用nexts数组
        int[] nexts = getNext(str2);
        while (i < str1.length() && j < str2.length()) {
            if (str1.charAt(i) == str2.charAt(j)) {
                i++;
                j++;
            } else if (j == 0) {
                i++;
            } else {
                j = nexts[j];
            }
        }
        return j == str2.length() ? i - j : -1;
    }
}

nexts数组的求取

我们规定，nexts数组的前两个值分别为-1和0，因此我们从下标为2的位置开始继续填充nexts数组

假设i-1位置的值已知为cn，现在求i位置的值
根据i-1的值我们可以知道最长前缀和最长后缀，并在上图做了标识。我们只需要判断cn位置的值是否和i-1位置的值相等即可

1. 如果相等

if (str.charAt(i - 1) == cn) {
   nexts[i++] = ++cn;
}

2. 如果不相等
   
   即cn位置的字符不等于i-1位置的字符，则将cn移动到nexts[cn]指示的位置
   

接着进行比较，如果相等则nexts[i++] = ++cn,否则继续变换cn，直到cn不能再向前移动，来到第三种情况
3. 其他情况
即str[cn]!=str[i-1] && cn <= 0
这种情况下，直接nexts[i++]=0

获取nexts数组的完整代码如下：

    public static int[] getNext(String str2) {
        int len = str2.length();
        if (len == 1) {
            return new int[]{-1};
        }

        int[] nexts = new int[len];
        nexts[0] = -1;
        nexts[1] = 0;

        int cn = 0;
        for (int i = 2; i < len; i++) {
            if (str2.charAt(i - 1) == cn) {
                nexts[i++] = ++cn;
            } else if (cn > 0) {
                cn = nexts[cn];
            } else {
                nexts[i++] = 0;
            }
        }
        return nexts;
    }

KMP算法代码

/**
 * 判断str2是否在str1中，是则返回起始字符索引在str1中的索引，否则返回-1
 */
public class KMP {

    public static int getIndexOf(String str1, String str2) {
        if (str1 == null || str2 == null || str2.length() < 1 || str1.length() < str2.length()) {
            return -1;
        }
        int i = 0;
        int j = 0;
        int[] nexts = getNext(str2);
        while (i < str1.length() && j < str2.length()) {
            if (str1.charAt(i) == str2.charAt(j)) {
                i++;
                j++;
            } else if (j == 0) {
                i++;
            } else {
                j = nexts[j];
            }
        }
        return j == str2.length() ? i - j : -1;
    }

    public static int[] getNext(String str2) {
        int len = str2.length();
        if (len == 1) {
            return new int[]{-1};
        }

        int[] nexts = new int[len];
        nexts[0] = -1;
        nexts[1] = 0;

        int cn = 0;
        for (int i = 2; i < len; i++) {
            if (str2.charAt(i - 1) == cn) {
                nexts[i++] = ++cn;
            } else if (cn > 0) {
                cn = nexts[cn];
            } else {
                nexts[i++] = 0;
            }
        }
        return nexts;
    }

    public static void main(String[] args) {
        String str1 = "abcab124agf";
        String str2 = "abcab124agf";
        System.out.println(getIndexOf(str1, str2));
        System.out.println(str1.indexOf(str2));
    }
}