周志华西瓜书《机器学习》第三章线性模型
又好像很久更新了,但这几天我都有在学习哦~。一位同学和我说感觉我的笔记很多是对书本原文的再现,缺少自己的思考和重点提炼。我反思了一下好像真的是这样的呢,这样子写似乎的确是和原文没有多大的区别(而且敲那么多字非常的累)。
所以从这篇笔记开始我会挑选书中的重点来记录啦,对于个别比较难理解的公式也会单独拿出来推导,不再把时间花在重复劳动上。
在写文章方面我只是一个小白,希望大家多多包涵。
3.1基本形式
对于一个物体,线性模型通过学得各个属性的线性组合来对其进行预测:
f ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + . . . + w d x d + b f\left ( x \right )=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+...+w_{d}x_{d}+b f(x)=w1x1+w2x2+w3x3+...+wdxd+b
上式可以用向量形式 f ( x ) = w T x + b f\left ( x \right )=w^{T}x+b f(x)=wTx+b来进行简单表示。
当我们学习得到 w = ( w 1 ; w 2 ; w 3 . . . ; w d ; ) w=\left ( w_{1}; w_{2}; w_{3}...; w_{d};\right ) w=(w1;w2;w3...;wd;)和 b b b之后便可以将模型确定下来。
- 线性模型的应用范围比较有限,但我们可以在这几个基础上通过层级结构或高维映射得到功能更为强大的非线性模型。
- 在线性模型中, w w w直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性(comprehensibility) 。
3.2 线性回归
我们可以使用"线性回归" (linear regression)来学得一个模型从而对预测值做出准确的预测输出标记。
在线性回归中,我们试图学得: f ( x ) = w T x + b ≅ y i f\left ( x \right )=w^{T}x+b\cong y_{i} f(x)=wTx+b≅yi。在这里我们用均方误差来进行性能度量,直接让均方误差最小化便可求得结果。即:
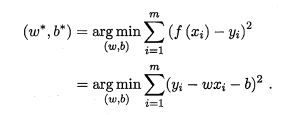
我们求解 w w w和 b b b让 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E_{\left ( w,b \right )}=\sum_{i=1}^{m}\left ( y_{i}-wx_{i}-b \right )^{2} E(w,b)=∑i=1m(yi−wxi−b)2实现最小值,这个过程可以通过对 w w w和 b b b求导来实现:
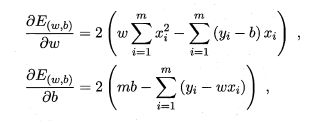
让两者分别为0便可以求得 w w w和 b b b的最优解:
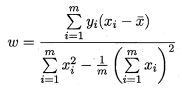

对于有多个属性的情况,我们可以用多元线性回归来实现问题的求解,将数据集用一个矩阵X来进行表示:

数据集的标记我们也可以用向量形式 y = ( y 1 ; y 2 ; . . . ; y m ; ) y=\left ( y_{1}; y_{2};...;y_{m};\right ) y=(y1;y2;...;ym;)来表示,从而可以得到和单属性相似的结果:

在上文部分,我们实现了单属性和多属性的线性回归推导,但在我们的实际生活中,线性回归的应用场景并不是那么常见,我们可以通过加一层映射来实现对y“衍生物”的逼近。
如 x x x到 y y y的实际映射为指数函数,我们令 y ‘ = l n y y^{`}=lny y‘=lny,那么x到 y ‘ y^{`} y‘的映射就变成了线性函数,我们可以继续用刚才讲过的那一部分知识来分析问题。得到 l n y = w T x + b lny=w^{T}x+b lny=wTx+b。
上式形式上仍然是线性回归,但是在实质上已经是在求解输入空间到输出空间的非线性函数映射。这里的对数函数起到了将线性回归模型的预测值和真实标记联系起来的作用。

更一般的,我们通过引入单调可微函数g(`)得到广义线性模型:
y = g − 1 ( w T x + b ) y=g^{-1}\left ( w^{T}x+b \right ) y=g−1(wTx+b)
3.3对数几率回归
这里我们首先要注意的是对数几率回归是用于处理分类问题吗,不是回归问题。
我们通过一个单调可微函数将分类任务的真实标记 y y y与线性回归模型的预测值联系起来。
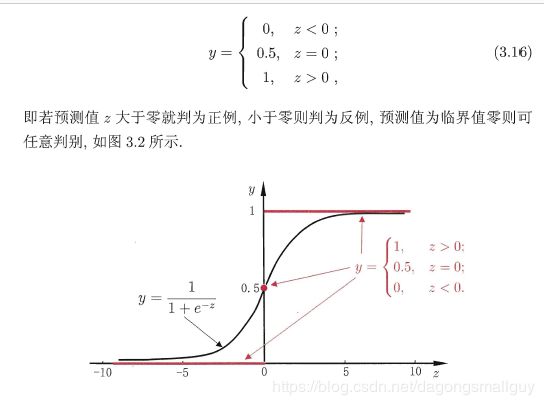
因为单位阶跃函数不连续,所以我们用对数几率函数来进行替代:
y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1,将对数几率函数作为我们之前提出的可微函数g(·),得:
y = 1 1 + e − ( w T x + b ) y=\frac{1}{1+e^{-\left ( w^{T}x+b \right )}} y=1+e−(wTx+b)1
上式可以推导为: l n y 1 − y = w T + b ln\frac{y}{1-y}=w^{T}+b ln1−yy=wT+b。
其中我们把 y y y看做是正例的可能性, 1 − y 1-y 1−y看成是反例的可能性,则=两者的比值 y 1 − y \frac{y}{1-y} 1−yy称为几率,反映了 x x x作为正例的相对可能性对几率取对数则得到"对数几率": l n y 1 − y ln\frac{y}{1-y} ln1−yy
接下来,我们就可以用“极大似然法”来对 w w w和 b b b进行估计。
3.4线性判别分析
线性判别分析(LDA)是一种经典的线性学习方法:给定一个训练样本,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别:
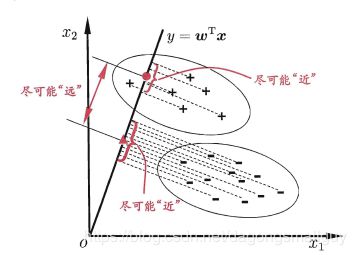
投影: w T μ 0 w^{T}\mu _{0} wTμ0和 w T μ 1 w^{T}\mu _{1} wTμ1
协方差: w T ∑ 0 w w^{T}\sum _{0} w wT∑0w和 w T ∑ 1 w w^{T}\sum _{1} w wT∑1w
欲使同类样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小;而欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大。
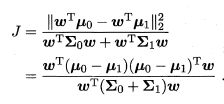
借助"类内散度矩阵" 和"类间散度矩阵",我们可以将上式转化为:
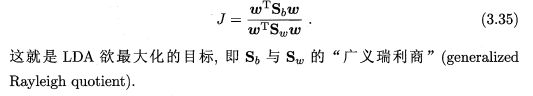
3.5 多分类学习
这一部分主要是讲述如何对数据集进行拆分换个集成。
有些二分类学习方法可直接推广到多分类,但在更多情形下,我们是基于一些基本策略,利用二分类学习器来解决多分类问题。
对于考虑N 个类别 C 1 , C 2 , C 3 . . . . C N C_{1},C_{2},C_{3}....C_{N} C1,C2,C3....CN, 多分类学习的基本思路是"拆解法"即将多分类任务拆为若干个二分类任务求解.
最经典的拆分策略有三种. “一对一” (One vs. One,简称OvO) 、“一对其余” (One vs. Rest ,简称OvR)和"多对多" (Many vs. Many,简称MvM)。
3.6类别不平衡问题
类别不平衡(class-imbalance)就是指分类任务中不同类别的训练样例数目差别很大的情况。
当训练集中正、反例的数目不同时,我们直接拿预测几率和观测几率进行比较就可以得出结论。如正例数目为 m + m^{+} m+,反例数目为 m − m^{-} m−,则观察几率为 m + m − \frac{m_{+}}{m_{-}} m−m+,当分类器的预测几率高于观测几率便可以判断为正例:
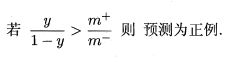
具体与上文的判别方法进行结合,我们只需要对预测值进行调整即可:
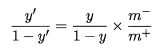
也就是我们常说的“再缩放”