机器学习(周志华) 西瓜书 第三章课后习题3.5—— Python实现

机器学习(周志华) 西瓜书 第三章课后习题3.5—— Python实现

个人原创，禁止转载——Zetrue_Li

 

数据集：

复制下列数据并粘贴到记事本，保存为data.txt：

编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

Python代码：

# -*- coding: utf-8 -*-

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

def loadData(filename):
	dataSet = pd.read_csv(filename)
	return dataSet

# 对集合分类
def compute_X(dataSet):
	D0, D1 = dataSet.loc[dataSet['好瓜']=='否'], dataSet.loc[dataSet['好瓜']=='是']
	
	X0 = np.array(D0[['密度', '含糖率']])
	X1 = np.array(D1[['密度', '含糖率']])
	return X0, X1


# 计算均值向量
def compute_Mu(X0, X1):
	Mu0, Mu1 = np.zeros((X0.shape[1], 1)), np.zeros((X0.shape[1], 1))
	for x in X0:
		x = x.reshape(x.shape[0], 1)
		Mu0 += x

	for x in X1:
		x = x.reshape(x.shape[0], 1)
		Mu1 += x

	return Mu0/X0.shape[0], Mu1/X1.shape[0]

# 类内散度矩阵
def within_class_scatter_matrix(X0, X1, Mu0, Mu1):
	Covariance0, Covariance1 = np.zeros((X0.shape[1], X0.shape[1])), np.zeros((X1.shape[1], X1.shape[1]))
	for x in X0:
		x = x.reshape(x.shape[0], 1)
		dif = x - Mu0
		Covariance0 += np.dot(dif, dif.T)

	for x in X1:
		x = x.reshape(x.shape[0], 1)
		dif = x - Mu1
		Covariance1 += np.dot(dif, dif.T)

	return Covariance0 + Covariance1

# 计算omega矩阵
def compute_Omega(Sw, Mu0, Mu1):
	Omega = np.dot(np.linalg.inv(Sw), (Mu0-Mu1))
	return Omega

# 画图
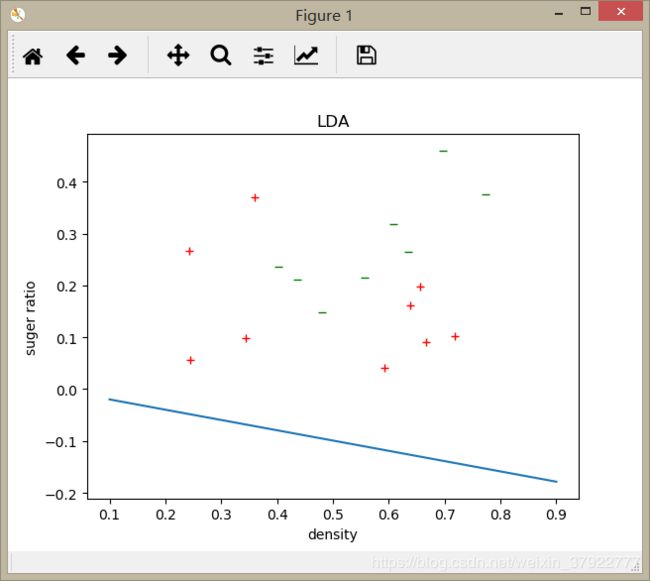
def draw_figure(Omega, X0, X1):
	for x in X0:
		plt.plot(x[0], x[1], '+r')

	for x in X1:
		plt.plot(x[0], x[1], '_g')

	# 斜率
	k = -Omega[0, 0] / Omega[1, 0]

	# 两点确定一直线
	line_x, line_y = [0.1, 0.9], []
	for x in line_x:
		line_y.append(k * x)

	plt.plot(line_x, line_y)

	plt.title('LDA')
	plt.xlabel('density')
	plt.ylabel('suger ratio')
	plt.show()

if __name__=="__main__":
	
	# 读取数据
	filename = 'data.txt'
	dataSet = loadData(filename)

	# 线性判别分析
	X0, X1 = compute_X(dataSet)
	Mu0, Mu1 = compute_Mu(X0, X1)
	Sw = within_class_scatter_matrix(X0, X1, Mu0, Mu1)
	Omega = compute_Omega(Sw, Mu0, Mu1)

	print('ω:')
	print(Omega)

	# 绘图 figure
	draw_figure(Omega, X0, X1)

实现结果：