机器学习(周志华) 西瓜书 第四章课后习题4.3—— Python实现
机器学习(周志华) 西瓜书 第四章课后习题4.3—— Python实现
-
实验题目
试编程实现基于信息熵进行划分选择的决策树算法,并为表4.3中数据生成一棵决策树。
-
实验原理
决策树基本算法:
基于信息熵增益的划分选择:
连续值处理:
缺省值处理
详见西瓜书4.4.2:缺失值处理讲解
-
实验过程
数据集获取
获取书中的西瓜数据集3.0,并存为data_3.txt
编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否
算法实现
数据定义,定义属性及其取值种类、类标签种类
读取数据函数:
叶节点选择标签函数:
判断D中样本在A上的取值是否相同函数
计算给定数据集的熵函数
计算按key划分的信息增益值函数
生成连续值属性的候选划分点集合T
计算样本D基于划分点t二分后的连续值属性信息增益
找出最大增益划分点
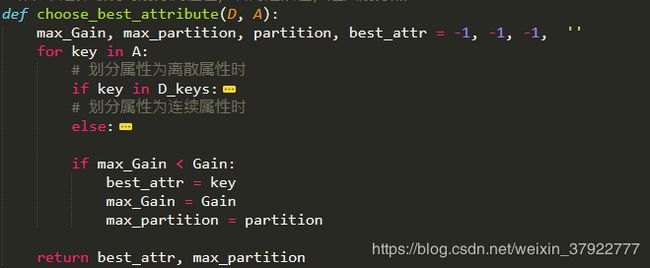
从A中选择最优的划分属性值,若为连续值,返回划分点
递归生成决策树
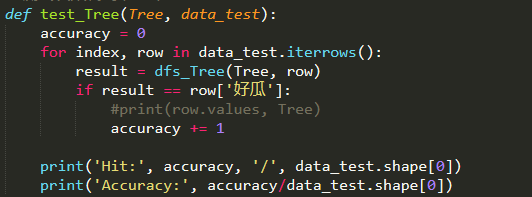
测试决策树的准确率
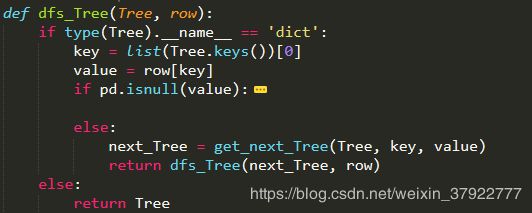
深度优先遍历,判断预测值
绘制树图的模块:
详见 https://blog.csdn.net/weixin_37922777/article/details/88821957
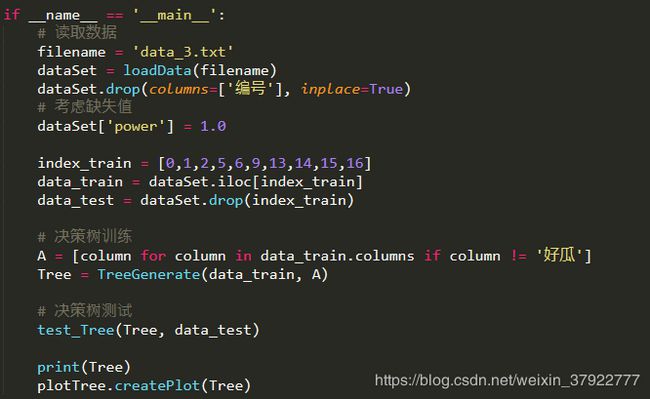
主函数:
-
实验结果
-
程序清单:
import json
import math
import plotTree
import numpy as np
import pandas as pd
D_keys = {
'色泽': ['青绿', '乌黑', '浅白'],
'根蒂': ['蜷缩', '硬挺', '稍蜷'],
'敲声': ['清脆', '沉闷', '浊响'],
'纹理': ['稍糊', '模糊', '清晰'],
'脐部': ['凹陷', '稍凹', '平坦'],
'触感': ['软粘', '硬滑'],
}
keys = ['是', '否']
# 读取数据
def loadData(filename):
dataSet = pd.read_csv(filename)
return dataSet
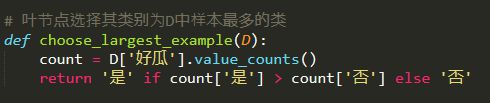
# 叶节点选择其类别为D中样本最多的类
def choose_largest_example(D):
count = D['好瓜'].value_counts()
return '是' if count['是'] > count['否'] else '否'
# 判断D中的样本在A上的取值是否相同
def same_value(D, A):
for key in A:
if key in D_keys and len(D[key].value_counts()) > 1:
return False
return True
# 计算给定数据集的熵
def calc_Ent(dataSet):
numEntries = dataSet['power'].sum()
Count = dataSet.groupby('好瓜')['power'].sum()
Ent = 0.0
for key in keys:
#print(Count[key])
if key not in Count:
Ent -= 0.0
else:
prob = Count[key] / numEntries
Ent -= prob * math.log(prob, 2)
return Ent
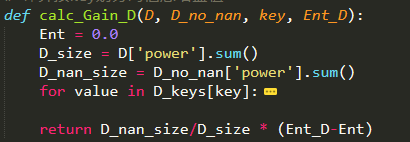
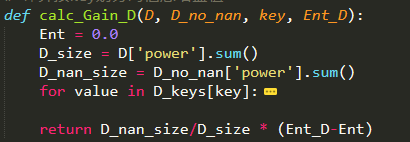
# 计算按key划分的信息增益值
def calc_Gain_D(D, D_no_nan, key, Ent_D):
Ent = 0.0
D_size = D['power'].sum()
D_nan_size = D_no_nan['power'].sum()
for value in D_keys[key]:
Dv = D.loc[D[key]==value]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size/D_nan_size * Ent_Dv
return D_nan_size/D_size * (Ent_D-Ent)
# 生成连续值属性的候选划分点集合T
def candidate_T(D, key, n):
L = set(D[key])
T = []
a, Sum = 0, 0
for value in L:
Sum += value
a += 1
if a == n:
T.append(Sum/n)
a, Sum = 0, 0
if a > 0:
T.append(Sum/a)
return T
# 计算样本D基于划分点t二分后的连续值属性信息增益
def calc_Gain_t(D, D_no_nan, key, t, Ent_D):
Ent = 0.0
D_size = D['power'].sum()
D_nan_size = D_no_nan['power'].sum()
Dv = D.loc[D[key]<=t]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size/D_nan_size * Ent_Dv
Dv = D.loc[D[key]>t]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size/D_nan_size * Ent_Dv
return D_nan_size/D_size * (Ent_D-Ent)
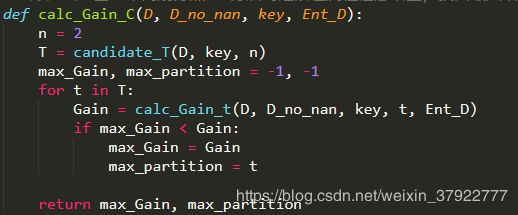
# 计算样本D基于不同划分点t二分后的连续值属性信息增益,找出最大增益划分点
def calc_Gain_C(D, D_no_nan, key, Ent_D):
n = 2
T = candidate_T(D, key, n)
max_Gain, max_partition = -1, -1
for t in T:
Gain = calc_Gain_t(D, D_no_nan, key, t, Ent_D)
if max_Gain < Gain:
max_Gain = Gain
max_partition = t
return max_Gain, max_partition
# 从A中选择最优的划分属性值,若为连续值,返回划分点
def choose_best_attribute(D, A):
max_Gain, max_partition, partition, best_attr = -1, -1, -1, ''
for key in A:
# 划分属性为离散属性时
if key in D_keys:
D_no_nan = D.loc[pd.notna(D[key])]
Ent_D = calc_Ent(D_no_nan)
Gain = calc_Gain_D(D, D_no_nan, key, Ent_D)
# 划分属性为连续属性时
else:
D_no_nan = D.loc[pd.notna(D[key])]
Ent_D = calc_Ent(D_no_nan)
Gain, partition = calc_Gain_C(D, D_no_nan, key, Ent_D)
if max_Gain < Gain:
best_attr = key
max_Gain = Gain
max_partition = partition
return best_attr, max_partition
# 函数TreeGenerate 递归生成决策树,以下情形导致递归返回
# 1. 当前结点包含的样本全属于一个类别
# 2. 当前属性值为空, 或是所有样本在所有属性值上取值相同,无法划分
# 3. 当前结点包含的样本集合为空,不可划分
def TreeGenerate(D, A):
Count = D['好瓜'].value_counts()
if len(Count) == 1:
return D['好瓜'].values[0]
if len(A)==0 or same_value(D, A):
return choose_largest_example(D)
node = {}
best_attr, partition = choose_best_attribute(D, A)
D_size = D.shape[0]
# 最优划分属性为离散属性时
if best_attr in D_keys:
for value in D_keys[best_attr]:
Dv = D.loc[D[best_attr]==value].copy()
Dv_size = Dv.shape[0]
Dv.loc[pd.isna(Dv[best_attr]), 'power'] = Dv_size / D_size
if Dv.shape[0] == 0:
node[value] = choose_largest_example(D)
else:
new_A = [key for key in A if key != best_attr]
node[value] = TreeGenerate(Dv, new_A)
# 最优划分属性为连续属性时
else:
#print(best_attr, partition)
#print(D.values)
left = D.loc[D[best_attr] <= partition].copy()
Dv_size = left.shape[0]
left.loc[pd.isna(left[best_attr]), 'power'] = Dv_size / D_size
left_key = '<= ' + str(partition)
if left.shape[0] == 0:
node[left_key] = choose_largest_example(D)
else:
node[left_key] = TreeGenerate(left, A)
right = D.loc[D[best_attr] > partition].copy()
Dv_size = right.shape[0]
right.loc[pd.isna(right[best_attr]), 'power'] = Dv_size / D_size
right_key = '> ' + str(partition)
if right.shape[0] == 0:
node[right_key] = choose_largest_example(D)
else:
node[right_key] = TreeGenerate(right, A)
# plotTree.plotTree(Tree)
return {best_attr: node}
# 获得下一层子树分支
def get_next_Tree(Tree, key, value):
if key not in D_keys:
partition = float(list(Tree[key].keys())[0].split(' ')[1])
if value <= partition:
value = '<= ' + str(partition)
else:
value = '> ' + str(partition)
return Tree[key][value]
# 深度优先遍历,判断预测值
def dfs_Tree(Tree, row):
if type(Tree).__name__ == 'dict':
key = list(Tree.keys())[0]
value = row[key]
if pd.isnull(value):
result = {key: 0 for key in D_keys['好瓜']}
for next_key in Tree[key]:
next_Tree = Tree[key][next_key]
temp = dfs_Tree(next_Tree, row)
result[temp] += 1
return '是' if count['是'] > count['否'] else '否'
else:
next_Tree = get_next_Tree(Tree, key, value)
return dfs_Tree(next_Tree, row)
else:
return Tree
# 测试决策树的准确率
def test_Tree(Tree, data_test):
accuracy = 0
for index, row in data_test.iterrows():
result = dfs_Tree(Tree, row)
if result == row['好瓜']:
#print(row.values, Tree)
accuracy += 1
print('Hit:', accuracy, '/', data_test.shape[0])
print('Accuracy:', accuracy/data_test.shape[0])
if __name__ == '__main__':
# 读取数据
filename = 'data_3.txt'
dataSet = loadData(filename)
dataSet.drop(columns=['编号'], inplace=True)
# 考虑缺失值
dataSet['power'] = 1.0
index_train = [0,1,2,5,6,9,13,14,15,16]
data_train = dataSet.iloc[index_train]
data_test = dataSet.drop(index_train)
# 决策树训练
A = [column for column in data_train.columns if column != '好瓜']
Tree = TreeGenerate(data_train, A)
# 决策树测试
test_Tree(Tree, data_test)
print(Tree)
plotTree.createPlot(Tree)