《机器学习》周志华-Uzi
【第一章 绪论】
归纳与演绎
induction归纳:从特殊到一般的“泛化”(generalization)——归纳学习(inductive learning)
deduction演绎:从一般到特殊的“特化”(specialization)
奥卡姆剃刀(occam’s razor)
奥卡姆剃刀定律(Occam's Razor, Ockham's Razor)又称“奥康的剃刀”,它是由14世纪逻辑学家、圣方济各会修士
奥卡姆的威廉
(William of Occam,约1285年至1349年)提出。这个原理称为“如无必要,勿增实体”,即“简单有效原理”。正如他在《箴言书注》2卷15题说“切勿浪费较多东西去做,用较少的东西,同样可以做好的事情。”
“计算”的目的往往是数据分析,而数据科学的核心也恰是通过数据分析来获得价值。
大数据时代的三大关键技术:机器学习、云计算、众包(crowdsourcing)
【第二章 模型评估与选择】
评估方法:
1.留出法(hold-out)
2.交叉验证法(cross-validation)
k折交叉验证
(k-fold cross validation)
3.自助法(bootstrapping)
在初始数据量足够时,留出法和交叉验证法更常用一些。
调参(parameter tuning):
机器学习,两类参数:1.算法的参数-“超参数”,数目常在10以内-通常是人工设定多个参数候选值后产生模型
2.模型的参数-通过学习来产生多个候选模型
均是产生多个模型之后基于某种评估方法来进行选择
最终模型:模型选择完成后,学习算法和参数配置已选定,用所有数据重新训练模型。这才是我们最终提供的模型。
训练数据(训练集、验证集validation set) 测试数据
分类结果混淆矩阵:
| 预测结果 | ||
| 真实情况 | 正例 | 反例 |
| 正例 | TP(真比例) | FN(假反例) |
| 反例 | FP(假比例) | TN(真反例) |
查准率precision : P = TP/(TP+FP)
查全率recall : R = TP/(TP+FN)
F1 score :
F1 = 2*P*R/(P+R) = 2*TP/(样例总数+TP-TN)
F1是基于查准率与查全率的调和平均(harmonic mean)定义的:1/F1 = 1/2*(1/P+1/R)
与算数平均和几何平均相比,调和平均更重视较小值。
(例如:商品推荐系统,尽可能少打扰用户,查准率! 逃犯信息检索系统,尽可能少漏掉逃犯,查全率!)
(beta=1时,退化为F1;beta>1,recall有更大的影响;beta<1时,precision有更大的影响。
先在各混淆矩阵上分别计算出P、R,在计算平均值。就得到相应的“宏F1”。
宏F1 : macro-P = 1/n*sigma(Pi) macro-R = 1/n*sigma(Ri) macro-F1 = 2 * macro-P * macro-R /(macro-P + macro-R)
先将各混淆矩阵的对应元素进行平均,得到TPFPTNFN的平均值,再基于这些平均值计算出“微F1”。
微F1: micro-P = mean(TP)/[mean(TP) +mean(FP)] micro-R = mean(TP) / [mean(TP) + mean(FN)] micro-F1 = 2* micro-P * micro-R / (micro-P + micro-R)
ROC与AUC:
学习器:将测试样本进行排序,“最可能”是正例的排在最前面,“最不可能”是正例的排在最后面。分类过程相当于是以某个“截断点”(cut point)将样本分为两部分,前为正例,后为反例。若更重视“查准率”,选择更靠前的位置进行截断;若更重视“查回率”,选择更靠后的位置进行截断。
排序本身质量的好坏,体现了学习器“一般情况下”泛化性能的好坏。——> “ROC曲线”——Receiver Operating Characteristic “受试者工作特征”
比较性能:比较ROC曲线,难以比较时,比较roc曲线下的面积,即AUC(Area Under ROC Curve)—>
考虑的是样本的排序质量
代价敏感错误率与代价曲线:
不同类型的错误所造成的后果不同。为权衡不同类型错误所造成的不同影响,可为错误赋予“非均等代价”(unequal cost)。
二分类代价矩阵:
| 预测类别 | ||
| 真实类别 | 第0类 | 第1类 |
| 第0类 | 0 | cost01 |
| 第1类 | cost10 | 0 |
若将第0类判别为第1类所造成的损失更大,则cost01>cost10;损失程度相差越大,cost01、cost10值的差别越大。
非均等代价下,我们所希望的不再是简单的最小化错误次数,而是希望最小化“总体代价”(total cost)。 不使用ROC曲线,而使用“代价曲线”(cost curve)。
比较检验:
统计假设检验(hypothesis test)
t检验、交叉验证t检验、McNemar检验、Friedman检验与Nemenyi后续检验
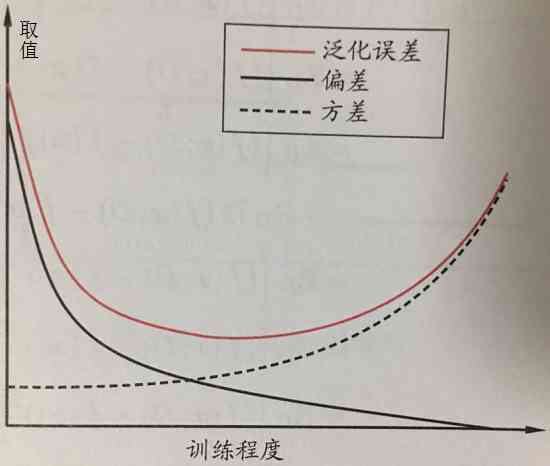
偏差与方差:
“偏差-方差分解”(bias-variance decomposition)是解释学习算法泛化性能的一种重要工具,试图对学习算法的
期望泛化错误率进行拆解。
—>泛化误差可分解为偏差、方差和噪声之和。
偏差:度量了学习算法的期望预测与真实结果的偏离程度,即刻画了
学习算法本身的拟合能力。
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了
数据扰动所造成的影响。
噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了
学习问题本身的难度。
偏差与方差是有冲突的—>“偏差-方差窘境”(bias-variance dilemma)
学习算法可控制
训练程度:决策树—>控制层数;神经网络—>控制训练轮数;集成学习方法—>控制基学习器个数
【第三章 线性模型】
非线性模型———>线性模型 + 层级结构 or 高维映射
对离散属性,若属性间存在“序”关系,可通过连续化将其转化为连续值,e.g.三值属性“高”“中”“低”——>转化为{1.0,0.5,0.0}
若属性间不存在“序”关系,假定有k个属性值,则通常转化为k维向量,e.g.属性“瓜类”的取值“西瓜”、“南瓜”、“黄瓜”——>转化为(0,0,1)、(0,1,0)、(1,0,0)
如何确定w,b ???——>关键在于如何衡量 f(x) 与 y 之间的差异。
均方误差(square loss,平方损失)——>回归任务中常用的性能度量, 因此, 均方误差最小化。
——>非常好的几何意义,对应了常用的“欧几里得距离”,即“欧式距离”(Euclidean Distance)。
——>基于
均方误差最小化来进行的模型求解 ——>“最小二乘法”(least square method) ——>线性回归中,就是试图找到一条直线,是所有样本到直线上的欧式距离之和最小。
广义线性模型: y = g
-1
(w
T
x + b),函数g称为“联系函数”。——>广义线性模型的参数估计常通过
加权最小二乘法
或
极大似然估计法
进行。
对数几率回归: 分类任务! ——> 只需找到一个
单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。
——>最理想的是“单位阶跃函数” (unit-step function / Heaviside function)
单位阶跃函数:
“sigmoid函数”——>将z值转化为一个接近0或1的y值,在z=0附近变化很陡 :
把sigmoid函数 作为 g
-1
代入,得到
——> 化简:
若将 y 视为 样本x 作为正例的可能性,则 1-y 视为 样本x 作为反例的可能性 ,两者的比值 y/(1-y)称为“几率”(odds),反映了x 作为正例的相对可能性。
对“几率”取对数,得到“对数几率”(log odds,亦称 logit) ,ln[y/(1-y)] ——>“对数几率回归”(logistic regression,亦称logit regression)。
虽然名字是“回归”,但实际是一种分类学习方法!!
优点:1.直接对分类可能性进行建模,无需事先假设数据分布。——> 避免了假设分布不准确所带来的问题
2.不仅预测出“类别”,而且得到近似概率预测,对许多需利用概率辅助决策的任务很有用
3.“对率函数”是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可直接用于求解最优解。
极大似然法 (maximum likelihood method)来估计w,b。对率回归模型最大化“对数似然”(loglikelihood) ,即令每个样本属于其真实标记的概率越大越好。
——>高阶可导连续凸函数。根据凸优化理论,经典的数值优化算法“
梯度下降法”(gradient descent method),“
牛顿法”(Newton method)等都可求得其最优解。
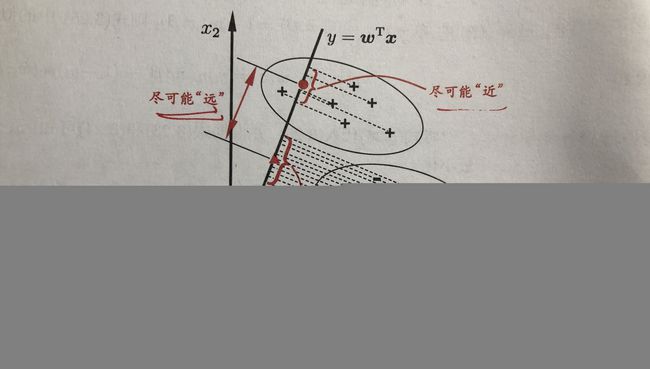
线性判别分析(LDA, Linear Discriminant Analysis), 亦称“Fisher 判别分析”。
LDA的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;
在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
多分类LDA将样本投影到d’维空间,d’通常远小于数据原有的属性数d。——>可通过这个投影来减小样本点的维数,且投影过程中使用了类别信息。——>因此,LDA也常被视为一种经典的
监督降维技术。
多分类学习:
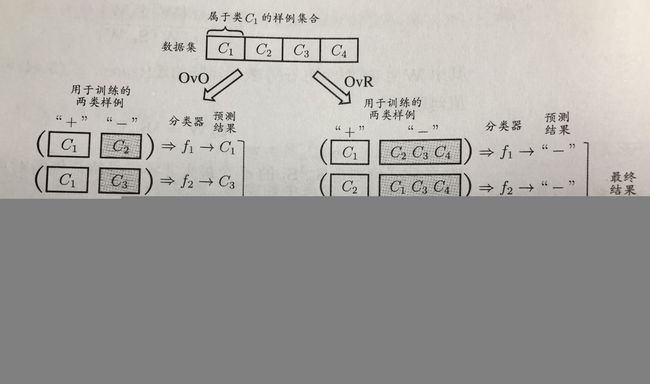
基本思路——>“拆解法”,即将多分类任务拆为若干个二分类任务求解。
最经典的三种拆解方法:1.“一对一” (One vs. One ,简称OvO) ——> N个类别两两配对,产生 N(N-1)/2 个二分类任务。
在测试阶段,新样本将同时提交给所有分类器,可得到 N(N-1)/2 个分类结果,最终结果投票产生,即把预测的最多的类别作为最终分类结果。
[需训练分类器数量多,但每次训练只用两个类的样例]
2.“一对其余” (One vs. Rest ,简称OvR) ——> 每次将一个类的样例作为正例,其余作为反例来训练N个分类器。
测试时,若仅一个分类器预测为正值,则对应的类别标记作为最终分类结果;若多个预测为正值,则通常考虑各分类器的预测置信度,选最大。
[需训练的分类器少,但每次训练需用所有类的样例]
类别很多时,选择OvO,这样训练时间开销通常比OvR更小。
至于预测性能,则取决于具体的数据分布,在多数情形下两者差不多。
3.“多对多”(Many vs. Many,简称MvM) ——> 正反类构造必须有特殊的设计,不能随意选取。
最常用的MvM技术:“纠错输出码”(Error Correcting Output Codes,简称ECOC)
——>将编码思想引入类别拆分,并尽可能在解码过程中具有容错性。
——>对同一个学习任务,ECOC编码越长,纠错能力越强。需训练分类器越多,计算、存储开销越大。
对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义。
对同等长度的编码,理论上,任意两个类别之间的编码距离越远,则纠错能力越强。
类别不平衡(class-imbalance):
基本策略——>“再缩放”(rescaling),亦称“再平衡”(rebalance)
“训练集是真实样总体的无偏采样”这个假设往往不成立。 e.g. 正例<<反例
现有技术大题有三类做法:1.直接对训练集里的反类样例进行“
欠采样”(undersampling),亦称“降采样”(downsampling),即去除一些反例使得正、反例数目接近。
——> 随机丢弃反例,可能丢失重要信息。代表算法:EasyEnsemble——> 利用集成学习机制,将反例划分为若干集合供不同学习器使用,对每个学习器都欠采样,全局看不会丢失重要信息。
2.对训练集里的正样例进行“
过采样”(oversampling),亦称“上采样”(upsampling),即增加一些正例使得正、反例的数目接近。
——> 不能简单的对初始正例样本进行重复采样,会导致严重的过拟合。
代表算法:SMOTE—— >对训练集里的正例进行插值来产生额外的正例。
3.直接基于原始训练就进行学习,但在用训练好的分类器进行预测时,将嵌入到其决策过程中,称为“
阈值移动”(threshold-moving)。
[欠采样法的时间开销通常远小于过采样法]
“再缩放”也是“代价敏感学习”(cost-sensitive learning)的基础。将m-/m+用cost+/cost-代替即可,其中cost+是将正例误分为反例的代价,cost-是将反例误分为正例的代价。
【第四章 决策树】
决策树(decision tree)的目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”(divide-and-conquer)策略。
关键:
如何选择最优划分属性。
希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”(purity)越来越高。
信息熵(information entropy)——>度量样本集合纯度
值越小,D的纯度越高。
信息增益(information gain)越大,则使用属性a来进行划分所获得的“纯度提升”越大。
ID3决策树学习算法(Iterative Dichotomiser):以信息增益为准则来选择划分属性。
信息增益准则对可取值数目较多的属性有所偏好。
C4.5决策树算法:不直接使用信息增益,而是使用“增益率”(gain ratio)来选择最优划分属性。
增益率准则对可取值数目较少的属性有所偏好。
C4.5并不是直接选择增益率最大的候选划分属性,而是使用一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
其中:
C4.5Rule决策树
CART决策树:使用“基尼指数”(Gini index)来选择划分属性。
Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。值越小,数据集D的纯度越高。
属性a的基尼指数定义:
剪枝(pruning):对付“过拟合”
基本策略:“预剪枝”(prepruning):在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
“后剪枝”(postpruning):先从训练集生成一颗完整的决策树,然后自底向上地对非结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能的提升,则将该子树替换为叶结点。
[后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般而言,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但训练时间开销大得多。]
连续值处理:
连续属性离散化技术:二分法(bi-partition),C4.5决策树算法中采用的机制
选取最优的划分点进行样本集合的划分。 注:与离散属性不同,若当前结点划分属性为连续属性,该属性还可作为其后代结点的划分属性。(e.g. 在父结点上使用了“密度<0.381”,不会禁止在子结点上使用“密度<0.294”)
缺失值处理:不完整样本,即样本的某些属性值缺失
1.如何在属性缺失的情况下进行划分属性的选择??
2.给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分??
权重
多变量决策树(multivariate decision tree):非叶结点不再是仅对某个属性,而是对属性的线性组合进行测试。
——>不像传统“单变量决策树”(univariate decision tree),不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
OC1算法:贪心地寻找每个属性的最优权制,在局部优化的基础上再对分类边界进行随机扰动以试图找到更好的边界
感知机树(Perceptron tree)
“增量学习”(incremental learning):通过调整分支路径上的划分属性次序来对树进行部分重构。 代表算法:
ID4、ID5R、ITI
——>可有效降低每次接收到新样本后的训练时间开销,但对多步增量学习模型后的模型会与基于全部数据训练而得的模型有较大差别。
【第五章 神经网络】
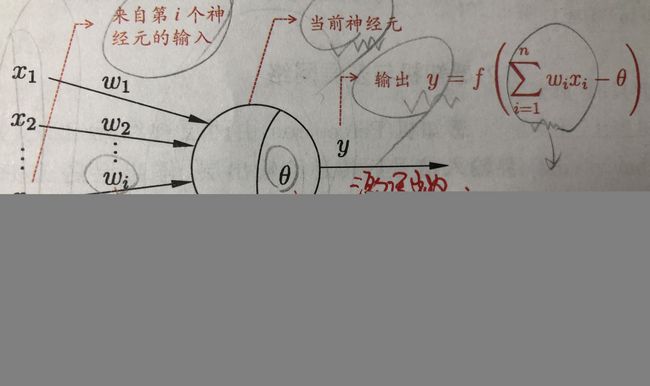
神经网络(neural networks):是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经网络系统对真实世界物体作出的交互反应。
“M-P神经元模型”
感知机(Perception)
多层前馈神经网络(multi-layer feedforward neural networks) “前馈”:指网络拓补结构上不存在环路或回路。
神经网络的学习过程,就是根据训练数据来调整神经元之间的“连接权”(connection weight)以及每个功能神经元的阈值——>神经网络“学“到的东西蕴含在
连接权和阈值中。
误差逆传播算法/反向传播算法(error BackPropagation,BP算法)
通常说“BP网络”,是指用BP算法训练的多层前馈神经网络。
累积误差逆传播算法(accumulated error backpropagation)
BP神经网络经常遭遇“过拟合”:1.“早停”(early stopping)——>训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阈值。
2.“正则化”(regularization)——>在误差目标函数中增加一个用于描述网络复杂度大的部分,例如连接权与阈值的平方和。
训练过程将会偏好比较小的连接权和阈值,使网络输出更加“光滑”,从而对过拟合有所缓解。
神经网络训练过程——>参数寻优过程,即在空间中寻找一组最优参数,使得E最小。
“局部极小”(local minimum) ——>参数空间内梯度为零的点,只要其误差函数值小于零点的误差函数值,就是局部极小点。
“全局最小”(global minimum)
基于梯度的搜索,是使用最为广泛的参数寻优方法。
“跳出”局部极小的策略:1.以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数。
2.“模拟退火”技术。每一步都以一定的概率接受比当前解更差的结果。在每次迭代中,接受“次优解”的概率要随着时间的推移而逐渐降低,从而保证算法的稳定性。(但也会造成“跳出”全局最小)
3.随机梯度下降
遗传算法(genetic algorithms)——>常用来训练神经网络以更好的逼近全局最小。
RBF网络(Radial Basis Function,径向基函数):1.确定神经元中心ci,常用随机采样、聚类等
2.利用BP算法等来确定参数wi和betai
ART网络(Adaptive Resonance Theory,自适应谐振理论) 竞争型学习(competitive learning)——>常用的无监督学习策略。 “胜者通吃”(winner-take-all)原则。
由比较层、识别层、识别阈值和重置模块构成。
计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离,距离最小者胜。
SOM网络(Self-Organizing Map,自组织映射) 竞争学习型的无监督神经网络,它能将高维输入数据映射到低维空间(通常为二维),同时保持输入数据在高维空间的拓补结构,
即将高维空间中的相似的样本点映射到网络输出层中的邻近神经元。
级联相关网络(Cascade-Correlation)——>结构自适应网络
Elman网络 “递归神经网络”(recurrent neural network)允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号。从而能处理与时间有关的动态变化。
Boltzman机
深度学习
【第六章 支持向量机】
间隔与支持向量
支持向量机(Support Vector Machine)
核函数(kernel function)
软间隔与正则化
硬间隔(hard margin)所有样本必须划分正确
软间隔(soft margin)允许支持向量机在一些样本上出错
替代损失(surrogate loss):hinge损失、指数损失(exponential loss)、对率损失(logistic loss)
支持向量回归(Support Vector Regression,SVR)
核方法(kernel methods):通过“核化”(即引入核函数)来将线性学习器拓展为非线性学习器。
“核线性判别分析”(Kernelized Linear Discriminant Analysis,KLDA)
【第七章 贝叶斯分类器】
贝叶斯决策论(Bayesian decision theory): 概率框架下实施决策
所有相关概率已知,如何基于这些概率和误判损失来选择最优的类别标记
决策树、BP神经网络、支持向量机 ——>判别式模型(discriminative models)
生成式模型(generatice models)
【第八章 集成学习】
分为两类:1.个体学习器间存在强依赖关系、必须串行生成的序列化方法——>Boosting
2.个体学习器间不存在强依赖性、可同时生成并行化方法——>Bagging和随机森林(Random Forest)
boosting:弱学习器提升为强学习器的算法。
bagging:
随机性来自:样本扰动
随机森林(random forest):对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性进行划分。k控制了随机性的引入程度。
(k=d,等于传统决策树;k=1,随机选择一个属性;推荐值 k = log
2d)
随机性来自样本扰动、属性扰动
结合策略: 加权平均法 、 投票法
多样性增强:数据样本扰动、输入属性扰动、输出表示扰动、算法参数扰动
【第九章 聚类学习】
聚类既能作为一个单独的过程,用于找寻数据内在的分布结构;也可作为分类等其他学习任务的前驱过程。
“性能度量”:“有效性指标”(validity index)
——>“簇内相似度”(intra-cluster similarity)高
“簇间相似度”(inter-cluster similarity)低
聚类性能度量外部指标:
Jaccard 系数 、FM指数 、Rand指数
聚类性能度量内部指标:
DB指数、 Dunm指数
距离计算: “距离度量”基本性质:非负性、同一性、对称性、直递性
有序属性——>闵可夫斯基距离
无序属性——>VDM(Value Difference Metric)
样本空间中不同属性的重要性不同时,使用加权距离。
基于某种形式的距离来定义“相似度度量”(similarity measure),距离越大,相似度越小。 很可能不满足“直递性” “非度量距离”
“距离度量学习”(distance metric learning)
原型聚类(prototype-based clustering)
k均值算法

无标记。
学习向量量化

加入标记,判别与标记是否一致,一致则靠近;否则远离。学习率yita可设置。
高斯混合聚类
密度聚类(density-based clustering):假设聚类结构能通过样本分布的紧密程度确定。
从样本密度的角度来考察样本之间的可连接度,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
基于“邻域”参数来刻画样本分布的紧密程度。
层次聚类(hierarchical clustering) ——>“自底向上” AGNES
——>“自顶向下” DIANA
改进后:BIRCH、ROCK等
聚类不存在客观标准
聚类集成(clustering ensemble):有效降低聚类假设与真实聚类结构不符、聚类过程中的随机性等带来的不利影响。
异常检测(anomaly detection):借助聚类或距离计算进行,如将远离所有簇中心的样本作为异常点,或将密度极低处的样本作为异常点。
【第十章 降维与度量学习】
k邻近学习: 最近邻近分类器,泛化错误率不超过贝叶斯最优分类器的错误率的两倍。
低维嵌入
主成分分析(Principal Component Analysis,简称PCA):无监督线性分类法(监督线性降维:线性判别分析LDA)
最近重构性、最大可分性,这是两种等价推导
舍弃是有必要的:一方面,样本的采样密度增大,这是降维的重要动机;另一方面,当数据收到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,将他们舍弃能在一定程度上起到去躁的效果。
核化线性降维:
核主成分分析(kernelized PCA,简称KPCA) 需对所有样本求和,因此它的计算开销大。
流形学习(manifold learning):“流形”是在局部与欧氏在局部具有欧氏空间的性质,能用欧氏距离来进行距离计算。
——>等度量映射(Isometric Mapping,简称Isomap):得到训练样本在低维空间的坐标。
(对于新样本,将训练样本的高维空间坐标作为输入,低维空间坐标作为输出,训练一个回归学习器来对新样本的低维空间坐标进行预测)
近邻连接图上,计算两点的最短路径,Dijkstra算法或Floyd算法,得到任意两点间的距离。
近邻图的构建:指定近邻点的个数、指定距离阈值
E
——>局部线性嵌入(Locally Linear Embedding,简称LLE):试图保持邻域内样本之间的线性关系。
度量学习:
“学习”出一个合适的度量。
【第十一章 特征选择与稀疏学习】
常见的特征选择方法:过滤式选择(filter):Relief(Relevant Features)-二分类问题 指定阈值或预选取的特征个数k,主要是设计“相关统计量”来度量特征的重要性。
Relief-F -多分类问题
包裹式选择(wrapper):直接把最终将要使用的学习器的性能作为特征子集的评价准则—>为给定学习器选择最有利于其性能、“量身定做”的特征子集。
LVW(Las Vegas Wrapper)- 在拉斯维加斯方法框架下使用随机策略来进行子集搜索,并以最终分类器的误差为特征子集的评价准则。
拉斯维加斯方法/蒙特卡罗方法 两个随机化方法。主要区别:有时间限制时,前者或者给出满足要求的解,或者不给出解;
后者一定给出解,但此解未必满足要求。无时间限制,则相同。
嵌入式选择(embedding):将特征选择过程与学习器训练过程融合为一体,两者在同一个优化过程中完成,即在学习器训练过程中 自动的进行了特征选择。
“岭回归(Ridge Regression)”、“LASSO(Least Absolute Shrinkage and Selection Operator)”、
ElasticNet回归(ElasticNet是Lasso和Ridge回归技术的混合体。它使用L1来训练并且L2优先作为正则化矩阵。)
L1范数、L2范数正则化都有助于降低过拟合风险,但前者还会带来一个额外的好处:比后者更易获得“稀疏(spares)解”,即他求解的w会有更少的非零分量。
基于L1正则化的学习方法就是一种嵌入式特征选择方法,其特征选择过程与学习器的训练过程融为一体,同时完成。
L1正则化问题的求解:近端梯度下降(Proximal Gradient Descent,简称PGD
稀疏表示与字典学习:“字典学习”(dictionary learning)-侧重于学得字典的过程,亦称“稀疏编码”(sparse coding)- 侧重于对样本进行稀疏表达的过程。
压缩感知(compressed/compressive sensing):根据部分信息来恢复全部信息。—>如何利用信号本身所具有的稀疏性,从部分观测样本中恢复原信号。
—>分为“感知测量”:如何对原始样本进行处理以获得稀疏样本表示。涉及:傅立叶变换、小波变换、字典学习、稀疏编码等
和“重构恢复”:如何基于稀疏性从少量观测中恢复原信号(压缩感知的精髓)
奈奎斯特(Nyquist)采样定理,令采样频率达到模拟信号最高频率的两倍,则采样后的数字信号就保留了模拟信号的全部信息。
“限定等距性”(Restricted Isometry Property,简称RIP) “基寻踪去噪”(Basis Pursuit De-Noising)
矩阵补全(matrix completion)技术 半正定规划(Semi-Definite Programming,简称SDP)
——>直接催生了人脸识别的鲁棒性主成分分析和基于矩阵补全的协同过滤
【第十二章 计算学习理论】
泛化误差
经验误差
经验误差与泛化误差之间的逼近程度。
“不合”(disagreement)来度量他们之间的差别。
会用到几个常用的不等式:Jensen不等式、Hoeffding不等式、McDiarmid不等式
PAC学习(Probably Approximately Correct,简称PAC),即“概率近似正确”学习理论
有限假设空间:可分情形、不可分情形
VC维(Vapnik-Chervonenkis dimension) —— 度量假设空间的复杂度
增长函数(growth function) —— 表示假设空间H对m个示例所能赋予标记的最大可能结果数
对分(dichotomy)
打散(shattering)
基于VC维的泛化误差界是 分布无关(distribution-free)、数据独立(data-independent)的。
Rademacher复杂度
稳定性:泛化损失、经验损失、留一损失。 均匀稳定性(uniform stability)
【第十三章 半监督学习】
聚类假设(cluster assumption)
流行假设(manifold assumption)
纯(pure)半监督学习 —— 基于“开放世界”
直推学习(transductive learning) —— 基于“封闭世界”
生成式方法(generative methods) —— 模型假设必须准确,即假设的生成式模型必须与真实数据分布吻合
半监督SVM(Semi-Supervised Support Vector Machine,简称S3VM)
图半监督学习 —— 一方面,此类算法难以处理大规模数据;另一方面,由于构图过程仅能考虑训练样本集,难以盼知新样本在图中的位置。
基于分歧的方法(disagreement-based methods) —— “多视图学习”(multi-view learning)的代表
协同训练算法,使用不同的学习算法、使用不同的数据采样、使用不同的参数设置
半监督聚类 —— “必连”(must-link,必属于同一簇)和“勿连”(cannot-link,必不属于同一簇);监督信息是少量的有标记样本
【第十四章 概率图模型】
概率图模型(probabilistic graphical model):用图来表达变量相关关系的概率模型。以图为表示工具,最常见的是:用一个结点表示一个或一组随机变量,结点之间的边表示变量间的概率相关关系,即“变量关系图”。
根据边的性质不同,概率图模型可大致分为两类:
第一类:使用有向无环图表示向量间的依赖关系,称为有向图模型或贝叶斯网(bayesian network)
第二类:使用无向图表示变量间的相关关系,称为无向图模型或马尔科夫网(markov network)
隐马尔可夫模型(hidden markov model,简称HMM)是结构最简单的动态贝叶斯网(dynamic bayesian network),著名的有向图模型。主要用于:时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
马尔可夫随机场(markov random field,简称MRF) 典型的马尔科夫网。 —》无向图模型
有一组势函数(potential functions),亦称“因子”(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
局部马尔科夫性(local markov property)、成对马尔可夫性(pairwise Markov property)
条件随机场(conditional random field,简称CRF) 一种判别式无向图模型
生成式模型(隐马尔可夫模型、马尔可夫随机场)是直接对联合分布进行建模,
判别式模型(条件随机场)是对条件分布进行建模
链式条件随机场(chain-structured CRF)
概念图模型中最常用的采样技术是马尔可夫链蒙特卡洛(Markov chain monto carlo,简称MCMC):
先设法构造一条马尔可夫链,使其收敛至平稳分布恰为待估计参数的后验分布,然后通过这条马尔可夫链来产生符合后验分布的样本,并基于这些样本来进行估计。
Metropolis-Hastings(简称MH)算法 :基于“拒绝采样”(reject sampling)来逼近平稳分布p
【第十五章 规则学习】
序贯覆盖(sequential covering)
自顶向下、自底向上
剪枝优化
规则生成本质上是一个贪心搜索过程,需有一定的机制来缓解过拟合的风险,最常见的做法是剪枝(pruning)。
规则生长过程中,“预剪枝”;规则产生之后,“后剪枝”
基于某种性能度量指标来评估增、删逻辑文字前后的规则性能,或增、删规则前后的规则集性能,从而判断是否要剪枝。
后剪枝最常用的是“减错剪枝”(reduce error pruning,简称REF)
一阶规则学习
【第十六章 强化学习】
任务与奖赏:
“强化学习”(reinforcement learning)
强化学习的“策略”实际上相当于监督学习中的“分类器”或“回归器”,
“强化学习”在某种意义上可看作具有“延迟标记信息”的监督学习问题。
k摇臂赌博机
通过尝试来发现各个动作产生的结果,而没有训练数据告诉机器应当做哪个动作。
欲最大化单步奖赏需考虑两个方面:1、需要知道每个动作带来的奖励;2、要执行奖赏最大的动作。
一般情况下,一个动作的奖赏值是来自于一个概率分布,仅通过一次尝试并不能确切的获得平均奖赏值。
“仅探索”(exploration-only) :将所有的尝试机会平均分配给每个摇臂(即轮流按下每个摇臂),最后以每个摇臂各自的平均吐币概率作为其奖赏期望的近似估计
“仅利用”(exploitation-only):按下目前最优的(即到目前为止平均奖赏最大的)摇臂。
“探索-利用窘境”(exploration-exploitation dilemma):欲累计奖赏最大,则必须在探索与利用之间达成较好的折中。
e贪心算法
每次尝试时,以e的概率进行探索,即以均匀概率随机选取一个摇臂;以1-e的概率进行利用,即选择当前平均奖赏最高的摇臂。
平均奖赏更新:
Qn(k)=1/n[(n-1)*Qn-1(k)+Vn]
无论摇臂被尝试多少次都仅需记录两个值;已尝试次数n-1和最近平均奖赏Qn-1(k)
若摇臂奖赏的不确定性较大,需要较大的e值;若摇臂的不确定性较小,需要较小的e值。通常,令e取一个较小的常数,如0.1或0.01。
若尝试次数非常大,那么在一段时间后,摇臂的奖赏都能很好的近似出来,不再需要探索,这种情况下可让e随着尝试次数的增加而逐渐减小,例如,令e=1/t^0.5
有模型学习(model-based learning)
免模型学习(model-free learning)
蒙特卡洛强化学习
时序差分学习(temporal difference,简称TD)
模仿学习(imatation learning)
直接模仿学习
逆强化学习