关于 0.1+0.2 == 0.3 不成立的一些细节
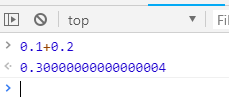
很早之前看到一关于js的问题,如下
实际上 0.1+0.2 != 0.3 这个问题不是js特有,来看一段java代码
@Test
public strictfp void test() {
System.out.println(0.1f + 0.2f == 0.3f);
System.out.println(0.1 + 0.2 == 0.3);
}程序的运行结果是
true
false这个问题应该是基础中的基础,众所周知,这是一个不可避免的浮点数精度丢失问题,同十进制一样,二进制中也会存在无限循环小数,而计算机对浮点数的表示通常是用 32 或 64 位的二进制,这使得在二进制的表达上必须采用“截断”的手段丢掉一些二进制位
下面我来分析为什么上面的运行结果是这样,由于Java不能直接查看浮点数的十六进制表达,所以用c语言来分析
1、IEEE754 标准
IEEE754是最广泛运用的浮点数表达的格式。Java里面有一个不怎么常见的strictfp关键字,用于修饰方法,被修饰的方法中的浮点运算都会严格遵守IEEE754规范。关于IEE754的细节,可以翻阅相关资料,这里就讨论主要的。
2、IEEE754 标准下浮点数的存储格式
浮点数的存储分为三个部分,s, e, f,对应符号(sign),指数(exp),有效数位(fraction)
对于float,s+e+f = 1+8+23
对于double,s+e+f=1+11+52
来看下面一段代码
准备两个函数,用于显示浮点数的二进制表达
void float_hex(float* f) {
int *p = (int *)f;
printf("%f -> %08x\n", *f, *p);
}
void double_hex(double* d){
int *p = (int *)d;
printf("%lf -> %08x %08x\n", *d, *p, *(p+1));
}main函数的调用
int main() {
float f = 0.1f;
float_hex(&f);
double d = 0.1;
double_hex(&d);
return 0;
}0011 1101 1100 1100 1100 1100 1100 1101
1)规范化表达
下面来验证一下,对于0.1,转化成二进制表达
0.000011001100110011....
规范化表达(类似于十进制的科学记数法)
1.100110011001100 x 2^-4
其中符号位0。
2)指数的表达
接下来的指数部分应该是-4,可是实际上存储的是是0111 1011,实际上这是移码的表达,移的是127,也就是指数部分存储的最终内容是127+(-4)=123,也就是0111 1011
3)有效部分截断时的四舍五入
有效数位部分按道理来讲是 1100 1100 1100 的循环直至截断,由于规范化表达,使得小数点左边的一位一定是1,所以这一位被省略了,剩下的就是1001 1001 1001的循环,由于有效只能表达23位,所以应该是(灰色表达要被丢弃的部分)
100 1100 1100 1100 1100 1100 1100 1100...
细心的人会注意到最后,四位并不是1100,而是1101,这是因为截断尾数时采用了四舍五入的方式,如果截断的部分第一位为1,说明截断部分的数值大于或等于上一位的1/2,因此向前进一位所表达的误差会更小,因此被截断的 1100 1100 1100.. 会对上一位产生进位影响,所以最后四位是1100 + 1 = 1101
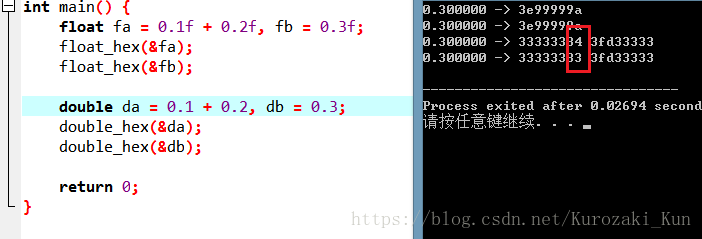
对于double型也是一样的方式,值得注意的是代码中显示的是 9999 9999a 3fb9 9999,
但实际上这个double的表达是 3fb9 9999 9999 9999a,代码打印的结果是因为这里采用大端存储的缘故
3、浮点数加法
指数不同的两个浮点数是不能直接相加的,拿
0.2的有效数位表达和0.1是相同的,但是指数部分比0.1的指数多1,因为恰好0.1x2=0.2,也可以写代码验证一下。
0.1的指数部分是-4,0.2指数部分是-3,小阶要向大阶“看齐”,0.1若要表示成指数为-3,就需要将有效数位整体右移,这样一来就能对有效数位相加
1.100 1100 1100 1100 1100 1101 0
0.110 0110 0110 0110 0110 0110 1
______________________________________
10.011 0011 0011 0011 0011 0011 1
橙色部分不会因为右移而丢失,因为在计算浮点数的时候会运用两个比float位数多的临时变量来计算,double也是
规范化,四舍五入后尾数为
001 1001 1001 1001 1010
指数为-2,表达出来是 0111 1101,0.1+0.2的结果应该表达为
0011 1110 1001 1001 1001 1001 1001 1010(3E99 999A)
4、为什么 0.1f+0.2f == 0.3f 成立
上面分析的是0.1+0.2都是浮点数表达,即0.1f+0.2f,结果是3E99 999A,直接用浮点数表达0.3f,也会得到结果3E99 999A,所以Java代码中第一个双等号的结果是true。因此,这个 true 的产生是二者截断后恰好都有进位的原因,并不是精确意义上的相等。
5、为什么0.1+0.2 == 0.3 不成立
用同样的方式分析double,给double型变量直接赋值 0.3 和赋值 0.1+0.2 会得到不一样的结果,具体原因是 0.1 + 0.2的时候尾数截断产生了进位,而直接表达 0.3 的时候没有,详细流程可以自己分析一下,这里不赘述。
因此Java代码中第二个双等号的结果是false
6、判断浮点数的运算结果
如果要想判断0.1+0.2==0.3,应该写成形如 Math.abs(0.1+0.2 - 0.3) < 1e-6 的形式。