《机器学习实战》第九章学习笔记(分类树回归CART)
一、CART(Classification And Regression Tree)
CART算法既可以用于分类还可以用于回归,CART树的生成就是递归构建二叉决策树的过程,对于回归树用平方误差最小化准则,对于分类树用基尼指数(Gini index)最小化准则,进行特征选择,生成二叉树。
1.1 回归树的生成
1.2 分类树的生成
1.2.1 基尼指数
1.2.2 分类树的生成
1.3 树回归的一般方法
(1) 收集数据:采用任意方法收集数据;
(2) 准备数据:需要数值型的数据,标称型数据应该映射成二值型数据;
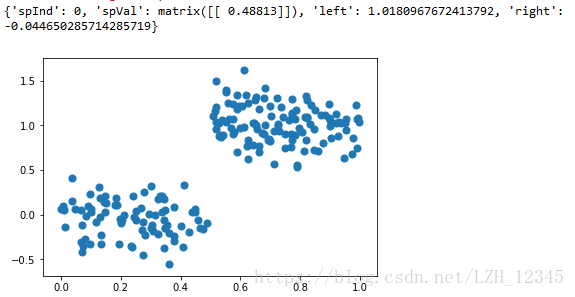
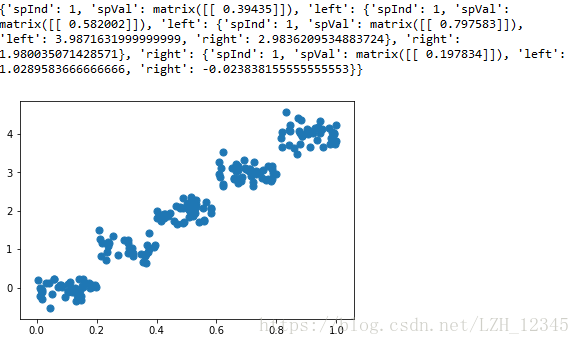
(3) 分析数据:绘出数据的二维可视化显示结果,以字典方式生成树;
(4) 训练算法:大部分时间都花费在叶节点树模型的构建上;
(5)测试算法:使用测试数据上的R^2(相关系数) 值来分析模型的效果;
(6)使用算法:使用训练出的树做预测,预测結果还可以用来做很多事情。
二、CART算法用于回归
2.1 代码实现
# -*- coding: utf-8 -*-
"""
Created on Mon May 7 19:27:00 2018
CART算法的实现代码
@author: lizihua
"""
from numpy import *
import matplotlib.pyplot as plt
#加载数据
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split("\t")
fltLine = list(map(float,curLine))
dataMat.append(fltLine)
return dataMat
#在给定的特征和特征值的情况下,通过数组过滤的方式将上述数据分成二个子集返回
def binSplitDataSet(dataSet, feature, value):
mat0 = dataSet[nonzero(dataSet[:,feature]>value)[0],:]
mat1 = dataSet[nonzero(dataSet[:,feature]<=value)[0],:]
return mat0,mat1
#创建叶结点,此时数据不能继续切分
def regLeaf(dataSet):
return mean(dataSet[:,-1])
#创建
def regErr(dataSet):
return var(dataSet[:,-1])*shape(dataSet)[0]
#errType:计算总方差(平方误差和)函数 = regErr
#ops:用户定义的参数构成的元组,用来完成树的构建,
#ops=(tolS,tolN),tolS:容许的误差下降值;tolN:切分的最小样本
#chooseBestSplit的目的是找到数据的最佳二元切分方式,若无,则返回None,并同时调用createTree产生叶结点
def chooseBestSplit(dataSet,leafType = regLeaf,errType = regErr,ops = (1,4)):
tolS = ops[0];tolN = ops[1]
#停止切分的条件1:若剩余的不同特征数目=1时,则退出
if len(set(dataSet[:,-1].T.tolist()[0])) ==1:
return None,leafType(dataSet)
m,n = shape(dataSet)
S = errType(dataSet)
bestS = inf; bestIndex = 0; bestValue = 0
for featIndex in range(n-1):
#for splitVal in set(dataSet[:,featIndex].T.A.tolist()[0]):
for splitVal in dataSet[:,featIndex]:
mat0,mat1 = binSplitDataSet(dataSet,featIndex,splitVal)
#当切分的数据集小于切分的最小样本tolN时,则退出循环
if (shape(mat0)[0]2.2 结果显示
三、树剪枝
![]()
3.1 预剪枝
前面CART实现算法中巳经进行了预剪枝操作。函数chooseBestSplit( )中通过输入(tolS,tolN)提前终止条件的过程,实际上是在进行一种所谓的预剪枝。
3.2 后剪枝
后剪枝则需要使用测试集和训练集,首先指定参数, 使得构建出的树足够大、足够复杂,便于剪枝。接下来从上而下找到叶节点,用测试集来判断将这些叶节点合并是否能降低测试误差。如果是的话就合并。
后剪枝的算法过程:
3.3 回归树后剪枝函数
3.3.1代码实现
#后剪枝函数
#判断是否是树,换言之,就是判断当前处理的节点是否是叶节点
def isTree(obj):
return (type(obj).__name__ == 'dict')
#从上往下遍历树直到叶节点为止,若找到两个叶节点,则计算它们的平均值
#该函数对树进行塌陷处理,即返回树的平均值
def getMean(tree):
if isTree(tree['right']):
tree['right'] = getMean(tree['right'])
if isTree(tree['left']):
tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
#后剪枝函数:两个参数:tree:代剪枝的树,testData:剪枝所需测试数据
def prune(tree,testData):
#判断测试集是否为空,空则返回树的均值,否则,对测试数据进行切分
if shape(testData)[0]==0:
return getMean(tree)
#判断分支是子树还是节点,若是子树,则调用prune函数进行剪枝
if (isTree(tree['right'])) or (isTree(tree['left'])):
lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
if isTree(tree['left']):
tree['left'] = prune(tree['left'],lSet)
if isTree(tree['right']):
tree['right'] = prune(tree['right'],rSet)
#对左右分支进行剪枝之后,仍要检查分支是否仍是子树,若皆不是,则合并
if not isTree(tree['left']) and not isTree(tree['right']):
lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
#计算合并前的误差平方和
errorNoMerge = sum(power(lSet[:,-1]-tree['left'],2))+sum(power(rSet[:,-1]-tree['right'],2))
treeMean = (tree['left']+tree['right'])/2.0
#计算合并后的误差平方和
errorMerge = sum(power(testData[:,-1] - treeMean,2))
#若合并后的误差比不合并的误差小,则进行合并,反之,则不合并
if errorMerge < errorNoMerge:
print('merging')
return treeMean
else:
return tree
else:
return tree
if __name__ == "__main__":
dataSet2 = loadDataSet('ex2.txt')
dataMat2 = mat(dataSet2)
myTree = createTree(dataMat2,ops=(0,1))
dataTest = loadDataSet('ex2test.txt')
dataTestMat = mat(dataTest)
bestTree = prune(myTree,dataTestMat)
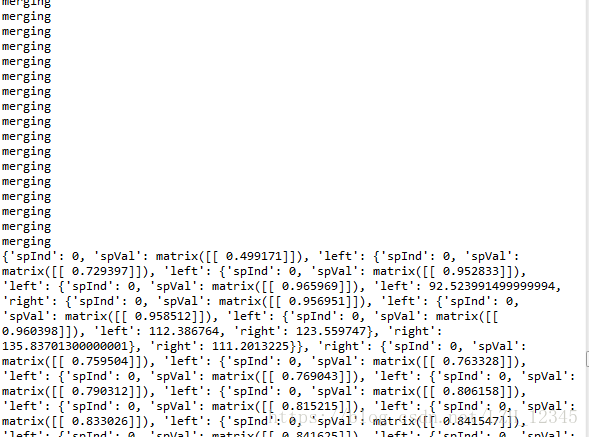
print(bestTree)3.3.2 部分结果显示
四、模型树
4.1 基本介绍
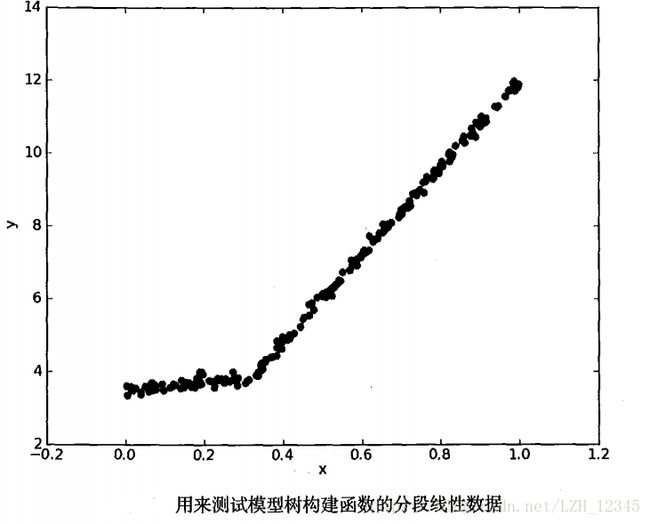
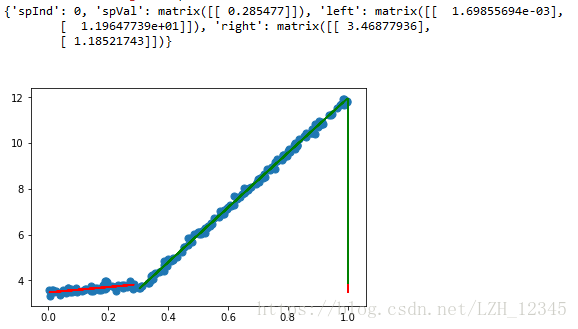
用树来对数据建模,除了把叶节点简单地设定为常数值之外, 还有一种方法是把叶节点设定为分段线性函数,这里所谓的分段线性(piecewise linear )是指模型由多个线性片段组成。如下图所示:
可以设计两条分别从0.0~0.3、从0.3~1.0的直线,于是就可以得到两个线性模型。因为数据集里的一部分数据(0.0~0.3)以某个线性模型建模,而另一部分数据(0.3~1.0)则以另一个线性模型建模,因此我们说采用了所谓的分段线性模型。
决策树相比于其他机器学习算法的优势之一在于结果更易理解。很显然,两条直线比很多节点组成一棵大树更容易解释。模型树的可解释性是它优于回归树的特点之一。另外,模型树也具有更髙的预测准确度。
模型树的误差计算:对于给定的数据集,应该先用线性的模型来对它进行拟合,然后计算真实的目标值与模型预测值间的差值。最后将这些差值的平方求和就得到了所需的误差。
4.2 代码实现
#线性模型函数,将被以下两个函数调用,其余过程与简单的线性回归函数过程一般
def linearSolve(dataSet):
m,n = shape(dataSet)
#初始化X,Y
X = mat(ones((m,n))); Y = mat(ones((m,1)))#create a copy of data with 1 in 0th postion
X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]
xTx = X.T*X
if linalg.det(xTx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\n\
try increasing the second value of ops')
ws = xTx.I * (X.T * Y)
return ws,X,Y
#生成叶结点模型
def modelLeaf(dataSet):#create linear model and return coeficients
ws,X,Y = linearSolve(dataSet)
return ws
#线性模型误差
def modelErr(dataSet):
ws,X,Y = linearSolve(dataSet)
yHat = X * ws
return sum(power(Y - yHat,2))
#绘制原始点的散点图以及拟合效果
def treePlot(xArr,yArr,tree):
xcord=[]
for i in range(len(xArr)):
xcord.append(xArr[i])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord,yArr, marker='o', s=50)
xArr1=xArr[xArr > tree['spVal']].T
xArr2=xArr[xArr <= tree['spVal']].T
x1 = insert(xArr1,0,values = ones(len(xArr1)),axis = 1)
x2 = insert(xArr2,0,values = ones(len(xArr2)),axis = 1)
yHat1 = x1*tree['left']
yHat2 = x2*tree['right']
plt.plot(x1,yHat1,c='g')
plt.plot(x2,yHat2,c='r')
plt.show()
if __name__ == "__main__":
dataSet3 = loadDataSet('exp2.txt')
dataMat3 = mat(dataSet3)
myTree = createTree(dataMat3,modelLeaf,modelErr,(1,10))
print(myTree)
treePlot(dataMat3[:,0],dataMat3[:,-1],myTree)