机器学习实战笔记-树回归
9.1 复杂数据的局部性建模
第3章使用决策树来进行分类。决策树不断将数据切分成小数据集,直到所有目标变量完全相 同 ,或者数据不能再切分为止。决策树是一种贪心算法,它要在给定时间内做出最佳选择,但并不关心能否达到全局最优。
树回归
优点:可以对复杂和非线性的数据建模。
缺点:结果不易理解。
适用数据类型:数值型和标称型数据。
第3章使用的树构建算法是ID3。ID3的做法是每次选取当前最佳的特征来分割数据,并按照该特征的所有可能取值来切分。也就是说,如果一个特征有4种取值,那么数据将被切成4份。一旦按某特征切分后,该特征在之后的算法执行过程中将不会再起作用,所以有观点认为这种切分方式过于迅速。另外一种方法是二元切分法,即每次把数据集切成两份。如果数据的某特征值等于切分所要求的值,那么这些数据就进人树的左子树,反之则进人树的右子树。
除了切分过于迅速外,ID3算法还存在另一个问题,它不能直接处理连续型特征。只有事先将连续型特征转换成离散型,才能在ID3算法中使用。但这种转换过程会破坏连续型变量的内在性质。而使用二元切分法则易于对树构建过程进行调整以处理连续型特征。具体的处理方法是:如果特征值大于给定值就走左子树,否则就走右子树。另外,二元切分法也节省了树的构建时间,但这点意义也不是特别大,因为这些树构建一般是离线完成,时间并非需要重点关注的因素。
CART是十分著名且广泛记载的树构建算法,它使用二元切分来处理连续型变量。对CART稍作修改就可以处理回归问题。第3章中使用香农熵来度量集合的无组织程度。如果选用其他方法来代替香农熵,就可以使用树构建算法来完成回归。
下面将实观CART算法和回归树。回归树与分类树的思路类似,但叶节点的数据类型不是离散型,而是连续型。
树回归的一般方法
(1) 收集数据:采用任意方法收集数据。
(2) 准备数据:需要数值型的数据,标称型数据应该映射成二值型数据。
(3) 分析数据:绘出数据的二维可视化显示结果,以字典方式生成树。
(4) 训练算法:大部分时间都花费在叶节点树模型的构建上。
(5)测试算法:使用测试数据上的R2值来分析模型的效果。
(6)使用算法:使用训练出的树做预测,预测結果还可以用来做很多事情
9.2 连续和离散型特征的树的构建
在树的构建过程中,需要解决多种类型数据的存储问题。与第3章类似,这里将使用一部字典来存储树的数据结构,该字典将包含以下4个元素。
□待切分的特征。
□待切分的特征值。
□右子树。当不再需要切分的时候,也可以是单个值。
□左子树。与右字树类似。
这与第3章的树结构有一点不同。第3章用一部字典来存储每个切分,但该字典可以包含两个或两个以上的值。而CART算法只做二元切分,所以这里可以固定树的数据结构。树包含左键和右键,可以存储另一棵子树或者单个值。字典还包含特征和特征值这两个键,它们给出切分算法.所有的特征和特征值
函数createTree()的伪代码大致如下:
找到最佳的待切分特征:
如果该节点不能再分,将该节点存为叶节点
执行二元切分
在右子树调用createTree()方法
在左子树调用createTree()方法
CART的实现代码如下:
from numpy import *
#注意,这次将xmat和ymat合在一起了,后面通过xmat[:,-1]获取xmat
#general function to parse tab -delimited floats
#assume last column is target value
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
#通过map(),将每一行的数据转换为float,在python3中需要再转换为list
fltLine = list(map(float,curLine)) #map all elements to float()
dataMat.append(fltLine)
return dataMat
#二分数据集
def binSplitDataSet(dataSet, feature, value):
#assume dataSet is NumPy Mat so we can array filtering
#通过数组过滤分离出dataSet中feature特征大于,小于等于value的数据
#我用的python3,书中的代码是python2,跑不成功,我自己把这两行调整了一下
mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:]
mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:]
return mat0,mat1
#leafType,求叶节点的函数
#errType,误差计算函数(分离出的左右子树对应ymat方差乘以子树数据集长度的累加)
#ops,元组,第一个值为误差阈值,第二个值为子树对应数据集的行数
def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
#通过最小化ymat方差选出拆分数据集的最好特征值
feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
#choose the best split
#if the splitting hit a stop condition return val
retTree = {}
retTree['spInd'] = feat
retTree['spVal'] = val
lSet, rSet = binSplitDataSet(dataSet, feat, val)
retTree['left'] = createTree(lSet, leafType, errType, ops)
retTree['right'] = createTree(rSet, leafType, errType, ops)
return retTree 书中createTree的解读:
该函数首先尝试将数据集分成两个部分,切分由函数chooseBestSplit()完成(这里未给出该函数的实现)。如果满足停止条件,chooseBestSplit()将返回None和某类模型的值,如果不满足停止条件,chooseBestSplit()将创建一个新的Python字典并将数据集分成两份,在这两份数据集上将分别继续递归调用createTree()函数。
测试代码如下:
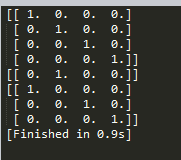
testMat = mat(eye(4))
print(testMat) mat0,mat1 = binSplitDataSet(testMat,1,0.5) print(mat0) print(mat1)9.3 将CART算法用于回归
为成功构建以分段常数为叶节点的树,需要度量出数据的一致性。可以通过平方误差的总差值求出数据的混乱度,也就是均方差乘以数据集中的样本数来得到。
9.3.1构建树
函数chooseBestSplit()只需完成两件事:用最佳方式切分数据集和生成相应的叶节点。
函数chooseBestSplit()伪代码如下:
对每个特征:
对每个特征值:
将数据集切分成两份 .
计算切分的误差
如果当前误差小于当前最小误差,那么将当前切分设定为最佳切分并更新最小误差
返回最佳切分的特征和阈值
回归树的切分函数,代码如下所示:
def regLeaf(dataSet):#returns the value used for each leaf
return mean(dataSet[:,-1])
def regErr(dataSet):
return var(dataSet[:,-1]) * shape(dataSet)[0]
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr,ops=(1,4)):
tolS = ops[0]; tolN = ops[1]
#if all the target variables are the same value: quit and return value
if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1
return None, leafType(dataSet)
m,n = shape(dataSet)
#the choice of the best feature is driven by Reduction in RSS error from mean
S = errType(dataSet)
bestS = inf; bestIndex = 0; bestValue = 0
#遍历每个特征
for featIndex in range(n-1):
#遍历每个特征的每个不同值,找出误差最小的特征值
for splitVal in set(dataSet[:,featIndex].flatten().A[0]):
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
#如果切分的子树长度太短,则跳过
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue
newS = errType(mat0) + errType(mat1)
if newS < bestS:
bestIndex = featIndex
bestValue = splitVal
bestS = newS
#if the decrease (S-bestS) is less than a threshold don't do the split
#如果误差下降值小于容许的误差下降至,那么合并这棵树为叶节点
if (S - bestS) < tolS:
return None, leafType(dataSet) #exit cond 2
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): #exit cond 3
return None, leafType(dataSet)
return bestIndex,bestValue#returns the best feature to split ones
#and the value used for that split9.3.2运行代码
from numpy import *
myDat = loadDataSet('ex00.txt')
myMat = mat(myDat)
myTree = createTree(myMat)
print(myTree)测试截图如下:

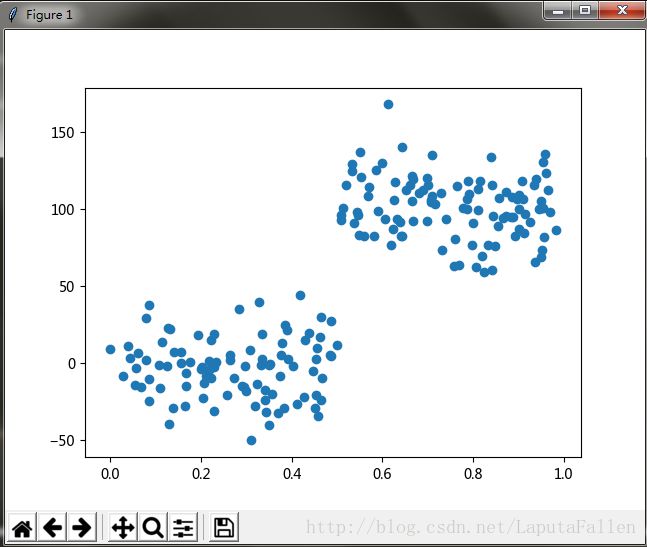
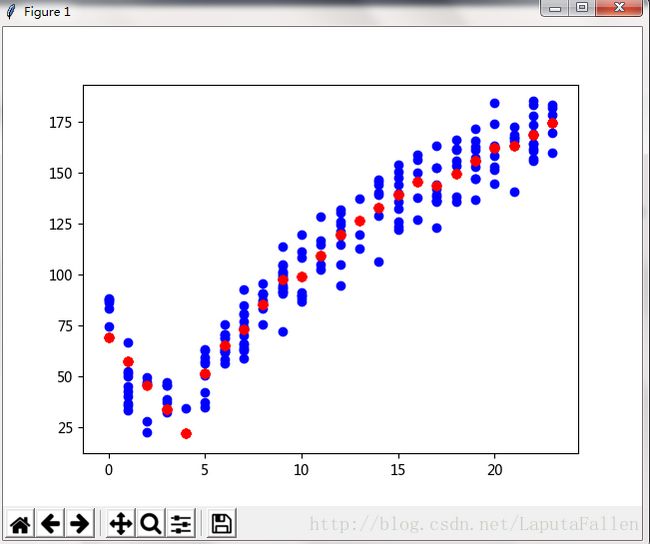
数据点分布如下:
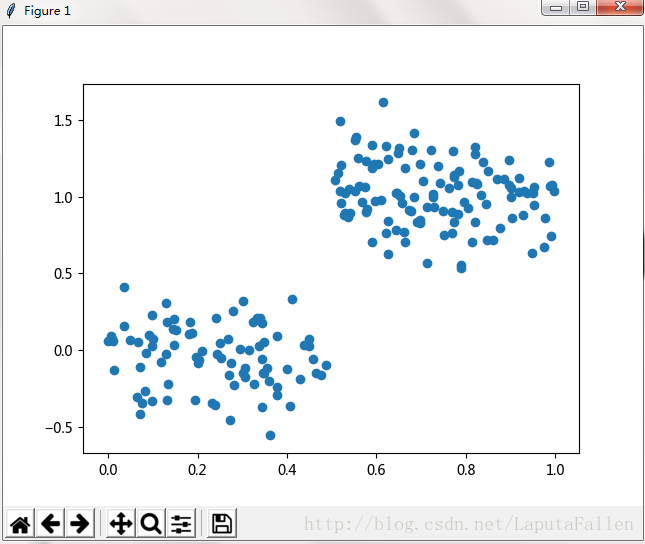
再看另一个多次切分的数据集,代码如下:
from numpy import *
myDat1 = loadDataSet('ex0.txt')
myMat1 = mat(myDat1)
print(createTree(myMat1))9.4 树剪枝
一棵树如果节点过多,表明该模型可能对数据进行了“过拟合”。通过降低决策树的复杂度来避免过拟合的过程称为剪枝(pnming)。其实本章前面巳经进行过剪枝处理。在函数chooseBestSplit()中的提前终止条件,实际上是在进行一种所谓的预剪枝(prepruning)操作。另一种形式的剪枝需要使用测试集和训练集,称作后剪枝(postpruning)。
9 . 4 . 1 预剪
上节两个简单实验的结果还是令人满意的,但背后存在一些问题。树构建算法其实对输人的参数tolS和tolN常敏感,如果使用其他值将不太容易达到这么好的效果。为了说明这一点,在Python提示符下输人如下命令:
from numpy import *
myDat = loadDataSet('ex00.txt')
myMat = mat(myDat)
myTree = createTree(myMat,ops = (0,1))
print(myTree)
print(getWidth(myTree))
#笔者自己写的获取树的宽度的方法
def getWidth(tree):
width = 0
if isTree(tree):
width += getWidth(tree['left'])
width += getWidth(tree['right'])
else:
return 1
return width测试截图如下:

与上节中只包含两个节点的树相比,这里构建的树过于臃肿,它甚至为数据集中每个样本都分配了一个叶节点。
如图所示的散点图,看上去与图9-1非常相似。但如果仔细地观察y轴就会发现,前者的数量级是后者的100倍。这将不是问题,对吧?现在用该数据来构建一棵新的树(数据存放在ex2.txt),在Python提示符下输人以下命令:
from numpy import *
myDat = loadDataSet('ex2.txt')
myMat = mat(myDat)
myTree = createTree(myMat)
print(myTree)
xArr = mat(myDat)[:,0].flatten().A[0]
yArr = mat(myDat)[:,1].flatten().A[0]
paint(xArr,yArr)
#paint为笔者自己写的绘图函数
def paint(xArr,yArr):
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xArr,yArr)
plt.show()我们发现,只因为y变为了原来的100倍,构建的树的叶子节点就比原来多了很多。产生这个现象的原因在于停止条件tolS对误差的数量级十分敏感。如果在选项中花费时间并对上述误差容忍度取平方值,或许也能得到仅有两个叶节点组成的树:
from numpy import *
myDat = loadDataSet('ex2.txt')
myMat = mat(myDat)
myTree = createTree(myMat,ops = (10000,4))
print(myTree)测试截图如下:

然而,通过不断修改停止条件来得到合理结果并不是很好的办法。事实上,我们常常甚至不确定到底需要寻找什么样的结果。
后剪枝,即利用测试集来对树进行剪枝。由于不需要用户指定参数,后剪枝是一个更理想化的剪枝方法。
9.4.2 后剪枝
使用后剪枝方法需要将数据集分成测试集和训练集。首先指定参数,使得构建出的树足够大、足够复杂,便于剪枝。接下来从上而下找到叶节点,用测试集来判断将这些叶点合并是否能降低测试误差。如果是的话就合并。
函数prune()的伪代码如下:
基于已有的树切分测试数据:
如果存在任一子集是一棵树,则在该子集递归剪枝过程
计算将当前两个叶节点合并后的误差
计算不合并的误差
如果合并会降低误差的话,就将叶节点合并
回归树剪枝函数代码如下:
def isTree(obj):
return (type(obj).__name__=='dict')
#从上往下遍历树直到叶节点为止。如果找到两个叶节点则计算它们的平均值。该函数对树进行塌陷处理(即返回树平均值)
def getMean(tree):
if isTree(tree['right']): tree['right'] = getMean(tree['right'])
if isTree(tree['left']): tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
def prune(tree, testData):
if shape(testData)[0] == 0: return getMean(tree) #if we have no test data collapse the tree
#if the branches are not trees try to prune them
if (isTree(tree['right']) or isTree(tree['left'])):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)
#if they are now both leafs, see if we can merge them
if not isTree(tree['left']) and not isTree(tree['right']):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
#对合并前后的误差进行比较。如果合并后的误差比不合并的误差小就进行合并操作,反之则不合并直接返回
errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\
sum(power(rSet[:,-1] - tree['right'],2))
treeMean = (tree['left']+tree['right'])/2.0
errorMerge = sum(power(testData[:,-1] - treeMean,2))
if errorMerge < errorNoMerge:
print("merging")
return treeMean
else: return tree
else: return tree测试代码如下:
myDat = loadDataSet('ex2.txt')
myMat2 = mat(myDat)
myTree = createTree(myMat2, ops=(0,1))
print(getWidth(myTree))
myDatTest = loadDataSet('ex2test.txt')
myMat2Test = mat(myDatTest)
prune(myTree,myMat2Test)
print("####################################################################################################")
print(getWidth(myTree))
#笔者自己写的计算叶子节点数目的函数
def getWidth(tree):
width = 0
if isTree(tree):
width += getWidth(tree['left'])
width += getWidth(tree['right'])
else:
return 1
return width测试截图如下:

由于直接看数字典可能不够清晰,因此我把它转化为对比宽度。可以发现效果还是很明显的但,没有像预期的那样剪枝成两部分,这说明后剪枝可能不如预剪枝有效。一般地,为了寻求最佳模型可以同时使用两种剪枝技术。
9.5模型树
用树来对数据建模,除了把叶节点简单地设定为常数值之外,还有一种方法是把叶节点设定为分段线性函数,这里所谓的分段线性(piecewise linear) 是指模型由多个线性片段组成。
考虑图9-4中的数据。如果使用两条直线拟合是否比使用一组常数来建模好呢?答案显而易见。可以设计两条分别从0.0~0.3、从0.3~1.0的直线,于是就可以得到两个线性模型。因为数据集里的一部分数据(0.0~0.3)以某个线性模型建模,而另一部分数据(0.3~1.0)则以另一个线性模型建模,因此我们说采用了所谓的分段线性模型。
决策树相比于其他机器学习算法的优势之一在于结果更易理解。很显然,两条直线比很多节点组成一棵大树更容易解释。模型树的可解释性是它优于回归树的特点之一。另外,模型树也具有更髙的预测准确度。
下面将利用树生成算法对数据进行切分,且每份切分数据都能很容易被线性模型所表示。该算法的关键在于误差的计算。应该怎样计算误差呢?前面用于回归树的误差计算方法这里不能再用。稍加变化,对于给定的数据集,应该先用线性的模型来对它进行拟合,然后计算真实的目标值与模型预测值间的差值。最后将这些差值的平方求和就得到了所需的误差。
模型树的叶节点生成函数,代码如下:
#根据ws计算公式,求出子树对应的ws矩阵
#helper function used in two places
def linearSolve(dataSet):
m,n = shape(dataSet)
#注意,x矩阵第一列全部为1,
X = mat(ones((m,n))); Y = mat(ones((m,1)))#create a copy of data with 1 in 0th postion
X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]#and strip out Y
xTx = X.T*X
if linalg.det(xTx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\n\ try increasing the second value of ops')
ws = xTx.I * (X.T * Y)
return ws,X,Y
#create linear model and return coeficients
def modelLeaf(dataSet):
ws,X,Y = linearSolve(dataSet)
return ws
#误差计算
def modelErr(dataSet):
ws,X,Y = linearSolve(dataSet)
yHat = X * ws
return sum(power(Y - yHat,2))测试代码如下:
myDat = loadDataSet('exp2.txt')
myMat2 = mat(myDat)
myTree = createTree(myMat2, modelLeaf,modelErr)
print(myTree) 测试截图如下:
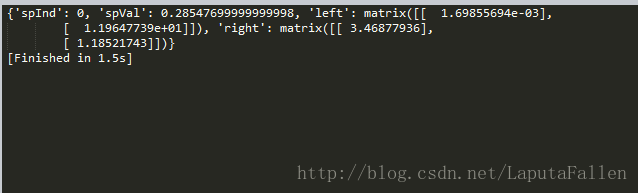
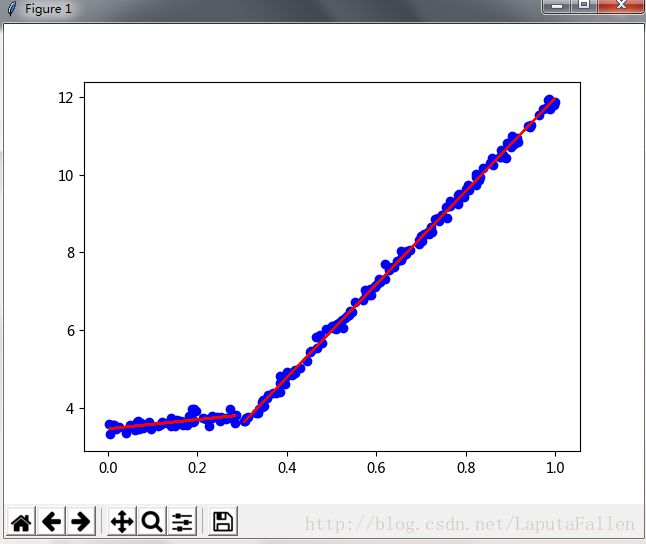
可以看到 ,该代码以0.285 477为界创建了两个模型,而图9-4的数据实际在0.3处分段。createTree ()生成的这两个线性模型分别是y=3 . 468+1.1852x和y=0 . 001 6985+11.964 77x,与用于生成该数据的真实模型非常接近。该数据实际是由模型y=3.5+1.0x和y=0+12再加上高斯噪声生成的。在图9-5上可以看到图9-4的数据以及生成的线性模型。
绘图代码如下:
myDat = loadDataSet('exp2.txt')
myMat2 = mat(myDat)
myTree = createTree(myMat2, modelLeaf,modelErr)
leftTree,rightTree = binSplitDataSet(myMat2,myTree['spInd'],myTree['spVal'])
#数据集对应的x,y
xArr = myMat2[:,0].flatten().A[0]
yArr = myMat2[:,1].flatten().A[0]
#得出左子树对应的x,以及推测的y
xMat1 = mat(ones((shape(leftTree)[0],2)))
xMat1[:,1] = leftTree[:,0]
xArr1 = leftTree[:,0].flatten().A[0]
yArr1 = (xMat1*myTree['left']).flatten().A[0]
#得出右子树对应的x,以及推测的y
xMat2 = mat(ones((shape(rightTree)[0],2)))
xMat2[:,1] = rightTree[:,0]
xArr2 = rightTree[:,0].flatten().A[0]
yArr2 = (xMat2*myTree['right']).flatten().A[0]
#xArr,yArr画散点图
#xArr1,yArr1和xArr2,yArr2画点图
paint(xArr,yArr,xArr1,yArr1,xArr2,yArr2)
#笔者自己定义的绘图函数,用来绘制点图和散点图
def paint(xArr,yArr,xArr1,yArr1,xArr2,yArr2):
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xArr,yArr,c="blue")
ax.plot(xArr1,yArr1,c="red")
ax.plot(xArr2,yArr2,c="red")
plt.show()模型树、回归树以及第8章里的其他模型,哪一种模型更好呢?一个比较客观的方法是计算相关系数,也称为 R2 值。该相关系数可以通过调用Numpy库中的命令corrcoef(yHat,y,rowvar=0)来求解,其中yHat是预测值,y是目标变量的实际值。
前一章使用了标准的线性回归法,本章则使用了树回归法,下面将通过实例对二者进行比较,最后用函数corrcoef()来分析哪个模型是最优的。
9 . 6 示例:树回归与标准回归的比较
前面介绍了模型树、回归树和一般的回归方法,下面测试一下哪个模型最好。本节首先给出一些函数,它们开以在树构建好的情况下对给定的输人进行预测,之后利用这些函数来计算三种回归模型的测试误差。这些模型将在某个数据上进行测试,该数据涉及人的智力水平和自行车的速度的关系。
用树回归进行预测的代码如下:
#回归树叶节点模型
def regTreeEval(model, inDat):
return float(model)
#模型树叶节点模型
def modelTreeEval(model, inDat):
n = shape(inDat)[1]
#注意,在X中添加第一列为1
X = mat(ones((1,n+1)))
X[:,1:n+1]=inDat
#返回线性模型预测的值
return float(X*model)
#递归整棵树,直到找到叶节点,然后通过modelEval对应的模型求出对应的预测值
def treeForeCast(tree, inData, modelEval=regTreeEval):
if not isTree(tree): return modelEval(tree, inData)
if inData[tree['spInd']] > tree['spVal']:
if isTree(tree['left']): return treeForeCast(tree['left'], inData, modelEval)
else: return modelEval(tree['left'], inData)
else:
if isTree(tree['right']): return treeForeCast(tree['right'], inData, modelEval)
else: return modelEval(tree['right'], inData)
#循环调用treeForeCast,得出预测值的助阵
def createForeCast(tree, testData, modelEval=regTreeEval):
m=len(testData)
yHat = mat(zeros((m,1)))
for i in range(m):
yHat[i,0] = treeForeCast(tree, mat(testData[i]), modelEval)
return yHat
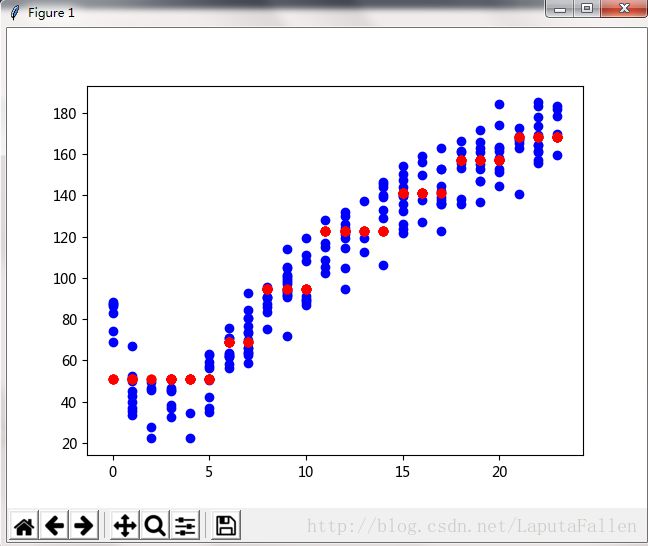
回归树测试代码如下:
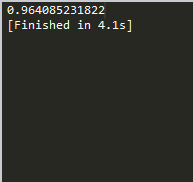
trainMat = mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat = mat(loadDataSet('bikeSpeedVsIq_test.txt'))
xArr = trainMat[:,0].flatten().A[0]
yArr = trainMat[:,1].flatten().A[0]
myTree = createTree(trainMat,ops=(1,20))
yHat = createForeCast(myTree,testMat[:,0])
xArr1 = testMat[:,0].flatten().A[0]
yArr1 = yHat.flatten().A[0]
print(corrcoef(yHat,testMat[:,-1],rowvar=0)[0,1])
#paint1为笔者自己写的绘图函数,画出训练数据点和预测数据点
paint1(xArr,yArr,xArr1,yArr1)线性回归树测试代码如下:
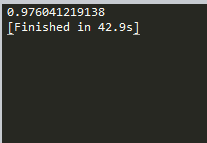
trainMat = mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat = mat(loadDataSet('bikeSpeedVsIq_test.txt'))
xArr = trainMat[:,0].flatten().A[0]
yArr = trainMat[:,1].flatten().A[0]
myTree = createTree(trainMat,modelLeaf,modelErr,(1,20))
yHat = createForeCast(myTree,testMat[:,0],modelTreeEval)
xArr1 = testMat[:,0].flatten().A[0]
yArr1 = yHat.flatten().A[0]
print(corrcoef(yHat,testMat[:,-1],rowvar=0)[0,1])
paint1(xArr,yArr,xArr1,yArr1)
我们知道, R2 值越接近1.0越好,所以从上面的结果可以看出,这里模型树的结果比回归树好 。下面再看看标准的线性回归效果如何,这里无须导人第8章的任何代码,本章已实现过一个线性方程求解函数linearSolve():
trainMat = mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat = mat(loadDataSet('bikeSpeedVsIq_test.txt'))
ws,X,Y = linearSolve(trainMat)
yHat = zeros((shape(testMat)[0],1))
print(ws)
for i in range(shape(testMat)[0]):
yHat[i] = testMat[i,0]*ws[1,0] + ws[0,0]
print(corrcoef(yHat,testMat[:,1],rowvar=0)[0,1])测试截图如下:

可以看到,该方法在 R2 值上的表现上不如上面两种树回归方法。所以,树回归方法在预测复杂数据时会比简单的线性模型更有效
本章后面章节是利用pythonGUI库Tkinter对回归模型比较,与机器学习关系不大,感兴趣的话可以查阅<机器学习实战>。