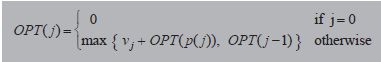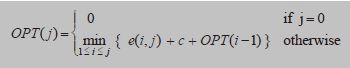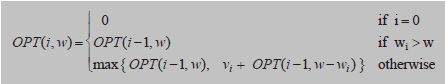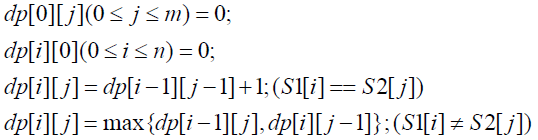算法课笔记系列(四)—— 动态规划
这两周都太忙,所以上周也没总结。这周一起补上。
上周讲的是Matroid,一个非常抽象的概念,中文翻译为“拟阵”。这个内容放到下一篇博文中。这篇总结一下这周讲的“动态规划(Dynamic Programming, 简称DP)”。动态规划可以应用在生物信息学,控制理论,信息理论,运筹学(Operations research)和计算机科学中的理论、图像、人工智能、编译器等等。
首先,对着之前的算法思路进行一个对比:
【贪心算法】是对问题增量地建立一个解决方法,仅考虑当前情况下的最优,并不断优化标准;
【分治算法】是将一个问题分解为若干个规模相等的子问题,解出子问题,然后将子问题的解进行组合,得到原问题的解;
而【动态规划】,则是将一个问题分解为有重合部分的子问题,将子问题的解不断地扩大成更大的子问题的解,最终得出满足条件的原问题的解。
针对课堂上讲的案例,这里做了一个list总结:
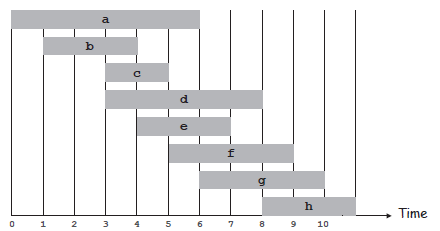
(1)Weighted Intervan Scheduling
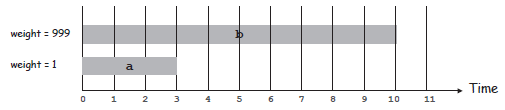
是不是觉得跟之前的贪心算法中的区间调度的例子很像?哈哈~其实就是一个问题,不过与之前贪心算法中不同的是,该区间调度是对每一个时间段给了一个权重,要解决的问题是同时兼容的任务的含有最大权重的子集。
当然,当所有任务的权重都等于1的时候,就变成典型的贪心算法了。我们回忆一下,在贪心算法中,对于该问题,我们是考虑最早结束时间,如果一个任务与之前选中的任务可以兼容,那么就加入到集合中。但是这种思路在权重任意并且不定的情况下是不可行的。反例如下:
对于该问题的考虑如下,首先按照任务的结束时间先后对任务进行排序编号,为f1,f2,…fn, 定义p(j)是任务i与任务j兼容的最大的索引项i。令OPT(j)为问题的最优解,包含任务1,2…任务j。
第一种情况:OPT选择任务j
此时,需要将任务j的权重加进来,不能加入不兼容的任务{p(j)+1,…,j-1},包含剩下的兼容的任务1,2,…p(j)问题的最优解。
第二种情况:OPT不选择任务j
这样,OPT一定包含剩下的兼容的任务1,2,…j-1问题的最优解。
针对该算法,使用暴力算法的话将会使得复杂度指数级增长,因此采用制表法/记忆法(Memoization), 将每一个子问题的结果放在一个缓存中;可以是一个查找表。
(2)Segmented Least Squares
给出一个平面中的n个点:(x1,y1), (x2, y2),…(xn,yn).目标是找到一条直线y = ax + b使得所有点与该直线上的垂直点的平方差的和最小。
(3)背包问题
有一个背包和n个物品,第i个物品的重量为wi(kg)>0,价值为vi>0。背包的容量为W(kg),目标是装满背包使得总价值最大。
这是最典型的动态规划的算法之一。
(4)RNA secondary Structure
有一个字符串B =b1b2,…bn. 全为字母{A, C, G, U}组成。因为RNA是单链的结构,因此可以扩展为回环,组成碱基对。这样的结构对于理解分子结构很重要,该结构称为RNA的二级结构。目标是给定一个分子B = b1b2,…bn,找出一个二级结构S能够最大化碱基对的数目
(5)序列对齐
给定两个字符串,找出两个字符串对齐的最小损耗(可gap)。如下图所示:
后面几个问题的分析暂时没写,先把结论放这里。最近实在是太忙,有时间会补上。
=====================分===割===线===============2016.4.4更新=============
前天晚上写得蛮匆促的,觉得没有很细致。现在补充一下。根据九度算法笔记整理。
动态规划的算法很多时候都是递推求解,像N阶楼梯上楼问题(一次可以走两阶或者一阶,问有多少种上楼方式,要求采用非递归)就是经典的递推求解问题。若我们把N分别等于1,2,3…的答案依次排列为一个数列,即需要求这个数列每一个数的值。定义f[n]为数列中第n个数,同时F[n]为台阶总数为n时的上台阶方式总数。首先,当数据规模较小时,我们可以直接得到答案,比如F[1] = 1,f[2]= 2。其次,我们必须确定数列之间的递推关系。当n大于2时,我们考虑每种上台阶方式的最后一步,到底是两步还是一步(只有这两种走法)。分别考虑这两种走法,即我们将此时所有的上楼梯方式按照最后一步走法的不同分成两类,分别确定这两类的上楼梯方式数目。经n-1阶到达n阶,因为其最后一步是确定的,所有其上楼梯方式数量与原问题中到达n-1阶的方式数量相同,同为F[n-1];同理,经n-2阶到达n阶,其上楼梯方式数量与原问题中到达n-2阶的方式数量相同,同为F[n-2]。这样,我们就确定了达到n阶楼梯总的上楼方式个数为F[n-1]和F[n-2]的和,即F[n] = F[n-1]+F[n-2]。这就是该数列的递推关系。初始值F[1] = 1,f[2]= 2,由此可以而出所有F[n]的值。
下面转到动态规划问题的其他一些例子。
1.最长递增子序列(LIS)
最长递增子序列是动态规划中最经典的问题之一。
在一个已知的序列{a1,a2,…an}中,取出若干数组成新的序列{ai1,ai2,…aim},其中下标i1,i2,…im保持递增,即新数列中的各个数之间依旧保持原数列中的先后顺序,那我们称新的序列{ai1,ai2,…aim}为原序列的一个子序列。若在子序列中,当下标ix>iy时,aix > aiy,那么我们称这个子序列为原序列的一个递增子序列。最长递增子序列问题,就是在一个给定的原序列中,求得其最长递增子序列长度。
有序列{a1,a2,…an},求其最长递增子序列。按照递推求解的思想,我们用F[i]代表递增子序列以ai结束时它的最长长度。当i较小时,我们容易直接得出其值,如F[1] = 1.那么,如何由已经求得的F[i]值推得后面的值呢。假设,F[1]到F[x-1]的值都已经确定,注意到,以ax结尾的递增子序列,除了长度为1的情况,其他情况中,ax都是紧跟在一个由ai(i
例:序列{1,4,3,2,6,5}的最长递增子序列长度的所有F[i]如下表:
总结一下,求最长递增子序列的递推公式为:
2.最长公共子序列(LCS)
另一个经典的动态规划问题是最长公共子序列。
与最长递增子序列的子序列定义相同,在字符串S中按照其先后顺序依次取出若干个字符,并将它们排列成一个新的字符串,这个字符串就被称为原字符串的子串。
有两个字符串S1和S2,求一个最长公共子串,即求字符串S3,它同时为S1和S2的子串,且要求它的长度最长,并确定这个长度。这个问题被我们称为最长公共子序列问题。
与求最长递增子序列一样,我们首先将原问题分割成一些子问题,我们用dp[i][j]表示S1中前i个字符与S2中前j个字符分别组成的两个前缀字符串的最长公共子串长度。显然的,当i,j较小时我们可以直接得出答案,如dp[0][j]必须等于0.那么,假设我们已经求得dp[i][j](0 <= i < x, 0 <=j < y)的所有值,考虑如何由这些值继而推得dp[x][y],求得S1前x个字符组成的前缀子串和S2前y个字符组成的前缀子串的最长公共子序列长度。
若S1[x] =S2[y],即S1中的第x个字符和S2中的第y个字符相同,同时由于他们都是各自前缀子串的最后一个字符,那么必须存在一个最长公共子串以S1[x]或S2[y]结尾,其他部分等价于S1中前x-1个字符和S2中前y-1个字符的最长公共子串。所以这个子串的长度比dp[x-1][y-1]又增加1,即dp[x][y] = dp[x-1][y-1] + 1.相反的,如果S1[x]≠ S2[y],此时其最长公共子串长度为S1中前x-1个字符和S2中前y个字符的最长公共子串长度与S1中前x个字符和S2中前y-1个字符的最长公共子串长度的较大者,即在两种情况下得到的最长公共子串都不会因为其中一个字符串又增加了一个字符长度发生改变。综上所述: ![]()
总结一下,最长公共子序列问题的递推条件:
假设有两个字符串S1和S2,其中S1长度为n,S2长度为m,用dp[i][j]表示S1前i个字符组成的前缀子串与S2前j个字符组成的前缀子串的最长公共子串长度,那么:
由这样的递推公式和显而易见的初始值,我们即能一次求得个dp[i][j]的值,最终dp[n][m]中保存的值即为两个原始字符串的最长公共子序列长度。
3.背包问题
背包问题有多种变形,0-1背包,完全背包和多重背包等。这里只阐述0-1背包的问题。
有个容量为V的背包和一些物品。这些物品分别有两个属性,体积w和价值v,每种物品只有一个。要求用这个背包装下价值尽可能多的物品,求该最大价值,背包可以不被装满。
因为最优解中,每个物品都有两种可能的情况,就是在背包中或者不在背包中(背包中有0个该物品或者1个),所以把这个问题称为0-1背包问题。
用dp[i][j]表示在总体积不超过j的情况下,前i个物品所能达到的最大价值。初始时,dp[0][j](0 <= j < V)为0.依据每种物品是否被放入背包,每个状态有两个状态转移的来源。若物品i被放入背包,设其体积为w,价值为v,则dp[i][j] = dp[i-1][j-w]+v,即在总体积不超过j-w时前i-1件物品可组成的最大价值的基础上再加上i物品的价值v;若物品不加入背包,则dp[i][j] = dp[i-1][j],即此时与总体积不超过j的前i-1件物品组成的价值最大值等价。选择他们之中的较大的值成为dp[i][j]的值。综上所述,0-1背包的状态转移方程为:
![]()
状态转移中可以发现,dp[i][j]的转移仅仅与dp[i-1][j-list[i].w]和dp[i-1][j]有关,即仅与二维数组中本行的上一行有关。因此,上面方程可以优化为一维: