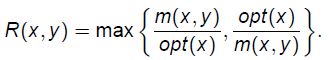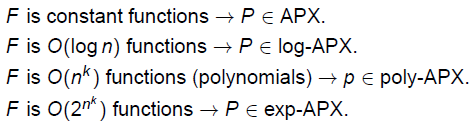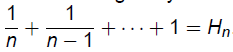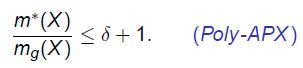算法课笔记系列（九）——近似算法（Part1）

这一周的内容是近似算法(Approximation Algorithm)。

对于许多的问题的算法，我们通常目标在于设计一个可以在多项式时间内运行的算法。然而，上一节的NP问题告诉我们这样的算法不一定存在。近似算法其实是针对NP难问题的一种退让，对于许多P不等于NP的最优化问题，无法在多项式时间内找到最优解。因此，如果可以只求一个我们可以接受的解，而不是非要最优解，那么可能存在一个多项式时间的算法。

因此，这里的“近似”其实就是针对最优化问题而言的。其主要应用也是用来解决最优化的问题，并且要求其时间花销为多项式级别的时间。

首先，提出一个NP的优化问题，即NPO问题。

        

不同的NOP问题的相似程度可能有非常大的差别。

一个NP优化问题P可以用一个四元组（I， Sol， m， goal）来表示，也就是：

I : I是P的实体的集合，可以在多项式时间内被识别；

Sol: 给定一个x∈  I， Sol(x)表示x的可能的解的集合；对于任意的y∈  Sol(x), |y|是|x|的多项式；给定任何|x|的多项式x和y，如果有y∈  Sol(x)，那么这个问题可以在多项式时间内决定。

m: 给定一个实例x∈  I，y∈  Sol(x)， y是x的一个可行解，m(x,y)表示y的值，并且，可以在多项式时间内被解决的函数

Goal ∈ {max, min}。表示这是一个最大化问题还是最小化问题。

下面定义一个NPO类：

类NPO是所有NP优化问题的集合。NPO问题的目标是，对于一个实体x，找到一个最优解，也就是一个可行解y使得m(x,y)=goal{m(x,y’): y’∈ Sol(x)}.

近似算法则是给定一个NP优化问题P=(I,Sol, m, goal)，一个算法A是对P的一个近似算法，如果给定任意的实例x∈  I， 它返回一个近似解，也就是一个有着保障质量的可行解A(x) ∈Sol(x) 。这里的保障的质量是只在近似与启发法之间的差异。

对于一个近似算法，我们关心以下两点：

1.      算法的时间复杂度（必须为多项式级的）

2.      解的近似程度（可能与算法设计、问题规模、输入实例等有关）

为了衡量解的近似程度，提出了近似比。

令P为一个NPO问题，给出一个实例x和x的一个可行解y，我们定义y对于x的一个性能比值为

         

r-近似的定义为：

给定一个优化问题P和一个P的近似算法A，A被称为一个r近似算法则对于P，如果给定P的任意实例x，近似算法A(x)的性能比界为r，即

下面定义F-APX，给定一类函数F，一个NPO问题P属于类F-APX如果一个r近似多项式时间算法A对于P存在，对于某个函数r∈ F。

           

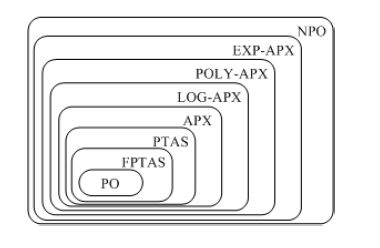
一个NPO问题P属于类PTAS如果一个算法A存在使得对于任意有理数ε> 0, 当将A应用到输入(x, ε), 它返回x的一个（1+ε）近似解在|x|的多项式时间内。通俗解释说，任意给定一个ε，这种“模式”都可以在多项式时间内完成，并且可以任意的逼近最优解。但是，随着ε变小，所花的时间可能急剧增多，比如O(n^2/ε)O(n^2/ε)。

这样的“模式”称为多项式时间近似模式（Polynomial-time approximation scheme，简称PTAS）。

FPTAS（Full PTAS）则是，如果一个算法A存在使得对于任意有理数ε> 0, 当将A应用到输入(x, ε), 它返回x的一个（1+ε）近似解在|x|和1/ε的多项式时间内.

如果P不等于NP，那么.

                    

       下面开始一些实际的例子。首先是从贪心算法的角度，下周将接触到从序列算法的角度。

使用贪心算法的角度的流程是，给定一个问题的实例指定一组条目。目标是决定满足问题限制的条目的一个子集，最大化或者最小化评价函数。具体步骤为，首先根据一些标准对这些条目进行排序，接着从空集开始增量的建立问题的解，一次只考虑一个条目，然后保持被选择了的条目的集合；当达到问题的限制条件时，终止。

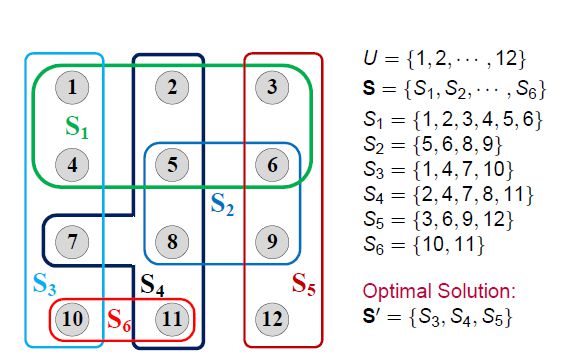
1.   集合覆盖问题

给定一个有n个元素的集合 ，U的一个子集的集合为 ，目标是找到一个子集能够覆盖U的所有元素。测量函数为计算选择子集的总成本，

         

算法实现为：

         

一个集合S的成本有效性是指它覆盖新元素时的平均成本，一个元素e的成本是当e被覆盖时的平均成本。贪心集合覆盖的时间复杂度为O（mn）。

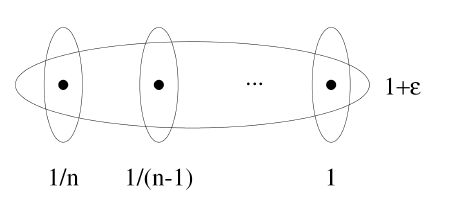
贪心集合覆盖时一个对于最小集合覆盖问题的Hn因子近似算法，其中，即调和数。（Log-APX）

                   

       最优覆盖的成本为1+ε，当贪心算法将输出覆盖的成本为

2.   最大背包问题

给定一个包含条目的有限集合X和一个正整数b，对于每一个xi∈ X，有一个价值pi∈ Z+，和一个大小ai∈ Z+。

我们目标是找到条目的一个集合使得,测量函数为计算选择条目的总价值测量函数为计算选择自己的总成本 .

              

贪心背包问题的复杂度为O（nlogn），对于该算法的近似比，事实上，贪心背包问题的解从最优值而言可以是任意远的。贪心背包的糟糕性能是因为算法并不能包含有着最高性能的利益的元素当最优解仅仅包含这个元素时。

3.   最大独立集问题

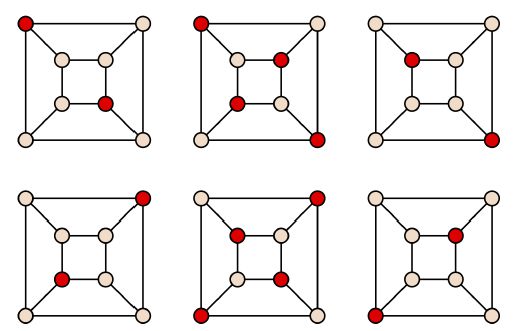
给定一个图G=（V,E），目标是为了在G上找到一个独立集, 使得对于任意的边 (u, v) ∈ E，有u ∉ V‘或者 v ∉ V‘。一个立方体有6个最大独立集（下图中红色结点标注）

               

                

给出一个有n个顶点和m条边的图G，令,贪心独立集的近似比为

 

Reference：

http://zhangxiaoyang.me/categories/intro-to-algorithms-tutorial/intro-to-algorithms-tutorial-9.html