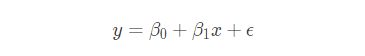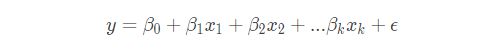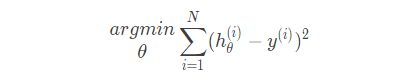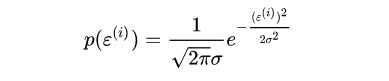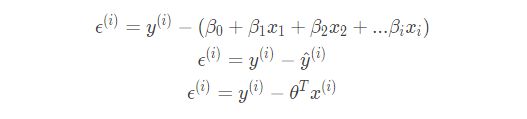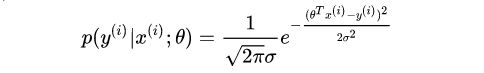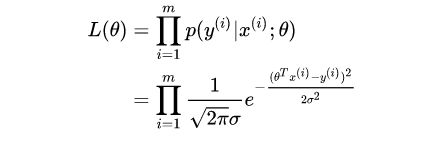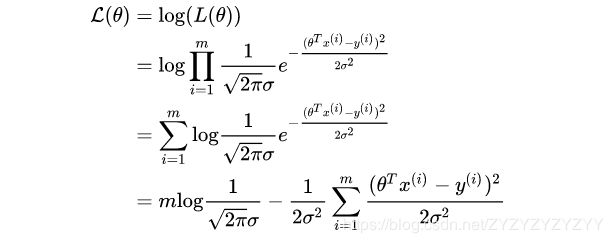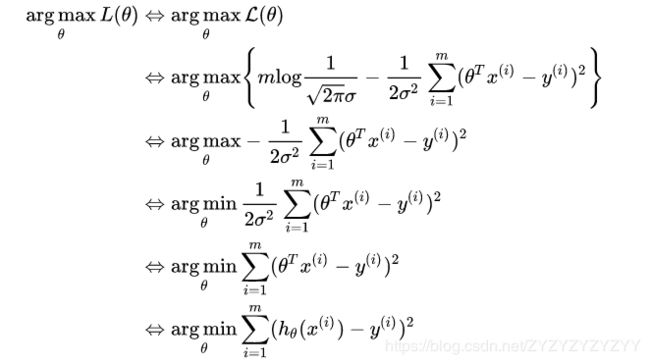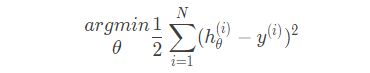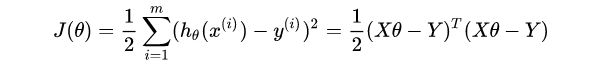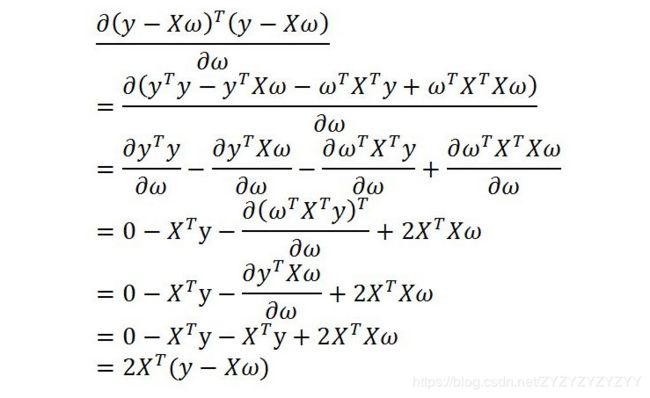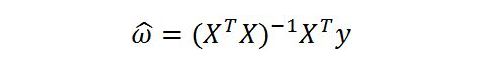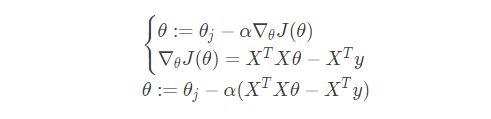机器学习学习笔记一：线性回归（一）

线性回归作为监督学习中经典的回归模型之一，是初学者入门非常好的开始。宏观上考虑理解性的概念，我想我们在初中可能就接触过，y=ax，x为自变量，y为因变量，a为系数也是斜率。如果我们知道了a系数，那么给我一个x，我就能得到一个y，由此可以很好地为未知的x值预测相应的y值。这很符合我们正常逻辑，不难理解。那统计学中的线性回归是如何解释的呢？

 

对于统计模型线性回归，我想从以下六个方面来展开，并分两篇文章进行详细解读：

• 线性回归模型定义

• 线性回归的损失函数

• 线性回归参数估计

• 线性回归预测

• 线性回归拟合优度

• 线性回归假设检验

• 线性回归诊断

 

▌线性回归模型定义

 

线性回归按变量数量的多少可以分为：一元线性回归（简单线性回归）和多元线性回归。

一元线性回归，也就是有一个自变量，其模型可以表示如下：

公式中参数解释如下：

x：自变量

y：因变量

β 0：截距

β 1：变量回归系数

ϵ：误差项的随机变量1

这些参数中，（β 0+β 1x）反映了由于x的变化而引起的y的线性变化；ϵ反映了除了x和y之间的线性关系之外的随机因素对y的影响，是不能由x和y之间的线性关系所解释的变异性。可以这么来理解ϵ：我们对y的预测是不可能达到与真实值完全一样的，这个真实值只有上帝知道，因此必然会产生误差，我们就用ϵ来表示这个无法预测的误差。

同样的，多元线性回归模型的表示如下：

 

我们通过引入了ϵ可以让模型达到完美状态，也就是理论的回归模型。但是我们要如何定义这个无法预测的误差项呢？为此，伟人们提出了一些假设条件：

在统计学中，高斯－马尔可夫定理陈述的是：在误差零均值，同方差，且互不相关的线性回归模型中，回归系数的最佳无偏线性估计（BLUE）就是最小方差估计。

 

总结一下，有如下几个主要的假设条件：

（1）误差项ϵ是一个期望为0的随机变量，即E(ϵ)=0

（2）对于自变量的所有值，ϵ的方差σ^2
都相同

（3）误差项ϵ是一个服从正态分布的随机变量，且相互独立，即ϵ~N(0,σ^2)

ϵ正态性意味着对于给定的自变量，因变量y也是一个服从正态分布的随机变量。根据回归模型的假设，有如下多元回归方程：

 

▌线性回归的损失函数

从样本数据考虑，如果想让我们预测值尽量准确，那么我们就必须让真实值与预测值的差值最小，即让误差平方和ϵ最小，用公式来表达即：

用平方而没用误差绝对值是因为：平方对于后续求导比较方便。

虽然我们得到了损失函数，但是如果从统计理论的角度出发来推导损失函数，我认为更有说服力，也能更好地理解线性回归模型，以及为什么开始要提出那些假设条件。

根据上面假设条件：ϵ 服从均值为0，方差为σ的正态分布，且独立，因此随机变量ϵ 的概率密度函数（正态分布的概率密度函数）为：

我们把前面的多元线性回归模型简单地变换一下，如下：

然后将得到的ϵ公式带入上面概率密度函数：

有了概率密度函数，我们自然会想到用最大似然估计推导损失函数：

 

然后我们将似然函数取对数，这样可以将概率密度的乘法转换为加法：

 

再然后我们对似然函数取最大值，即最大化似然函数：

这样我们就从统计理论的角度得到了我们要找的损失函数，与我们最小化误差平方和得到的结果是一样的，也从侧面证实了前面提出假设的正确性。因此，多元线性回归模型的损失函数为：

公式里的1/2对损失函数没有影响，只是为了能抵消求导后的乘数2。

▌线性回归参数估计

损失函数只是一种策略，有了策略我们还要用适合的算法进行求解。在线性回归模型中，求解损失函数就是求与自变量相对应的各个回归系数和截距。有了这些参数，我们才能实现模型的预测（输入x，给出y）。

对于误差平方和损失函数的求解方法有很多，典型的如最小二乘法，梯度下降等。下面我们分别用这两种方法来进行求解。

 

最小二乘法

最小二乘法可以将误差方程转化为有确定解的代数方程组（其方程式数目正好等于未知数的个数），从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。

我们将代数方程组用矩阵来代替可以简化推导过程，以及代码实现。

这里会涉及到矩阵求导的用法，详细介绍请看下面wiki的参考链接：

https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities

 

我们令上面得到的公式等于0，即可得到最终的求解：

 

Python中对于矩阵的各种操作可以通过Numpy库的一些方法来实现，非常方便。但在这个代码实现中需要注意：X矩阵不能为奇异矩阵，否则是无法求解矩阵的逆的。下面是手撸最小二乘法的代码实现部分。

def standRegres(xArr,yArr):
    """
    函数说明:计算回归系数w
    Parameters:
        xArr - x数据集
        yArr - y数据集
    Returns:
        ws - 回归系数
    """
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    #根据文中推导的公示计算回归系数
    xTx = xMat.T * xMat 
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws

 

梯度下降法

梯度下降是另一种常用的方法，可以用来求解凸优化问题。它的原理有别于最小二乘法，它是通过一步步迭代（与最小二乘法的区别在后面介绍）求解，不断逼近正确结果，直到与真实值之差小于一个阈值，从而得到最小化损失函数的模型参数值的。它的公式如下：

对于损失函数的梯度（即求偏导的过程），上面在最小二乘法部分已经给出推导过程和结果。不同的是，我们不会将公式等于0来求极值，而是带入上面梯度下面公式来迭代完成求解，以下是梯度下降矩阵形式的最终求解结果。

 

最小二乘法 vs 梯度下降法

通过上面推导，我们不难看出，二者都对损失函数的回归系数进行了求偏导，并且所得到的推导结果是相同的，那么究竟哪里不同呢？

如果仔细观察，可以观察到：最小二乘法通过使推导结果等于0，从而直接求得极值，而梯度下降则是将推导结果带入迭代公式中，一步一步地得到最终结果。简单地说，最小二乘法是一步到位的，而梯度下降是一步步进行的。

因而通过以上的异同点，总结如下

最小二乘法：

• 得到的是全局最优解，因为一步到位，直接求极值，因而步骤简单

• 线性回归的模型假设，这是最小二乘方法的优越性前提，否则不能推出最小二乘是最佳（即方差最小）的无偏估计

梯度下降法：

• 得到的是局部最优解，因为是一步步迭代的，而非直接求得极值

• 既可以用于线性模型，也可以用于非线性模型，没有特殊的限制和假设条件

▌线性回归预测

 

上面我们已经手撸了最小二乘法和梯度下降法求解误差平方和损失函数的过程，即我们通过以上算法已经得到了我们想要的参数值。当然，我们也可以使用statsmodels或者sklearn库中已经被封装好了的模型来进行预测。不过，为了更好的了解模型，优化算法，而不仅仅是做一个调包侠，我们最好对每种算法都自己实现一遍。

为了更好的说明整个建模到预测的过程，我们通过一个例子来详细说明。对于一个数据集，我们通过自己手撸的最小二乘法来建模，求解参数然后进行预测。

class LeastSquared(object):
    def __init__(self):
        self.xArr = []
        self.yArr = []
        self.params = []
        self.y_predict = []

    def fit(self,xArr,yArr):
        self.xArr = xArr
        self.yArr = yArr
        xMat = np.mat(xArr)
        yMat = np.mat(yArr).T
        xTx = xMat.T*xMat
        if np.linalg.det(xTx) == 0.0:
            print('矩阵为奇异矩阵')
        params = xTx.I*(xMat.T*yMat)
        self.params = params

    def predict(self,x_new):
        y_predict = x_new*self.params
        self.y_predict = y_predict
        return y_predict

 

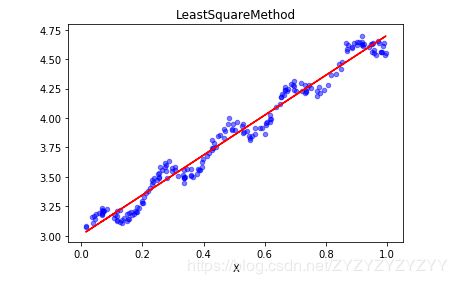
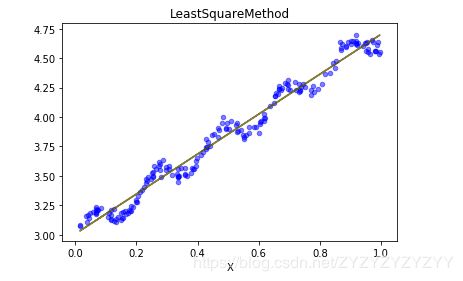
可以看到这是一个简单的二维平面，蓝色代表一个变量X和因变量Y的散点图，红色是我们通过最小二乘法拟合出来的直线。如果是多自变量，那么拟合结果将是一个平面，或者超平面。使用这个模型，我们就能对未知的X值进行预测。

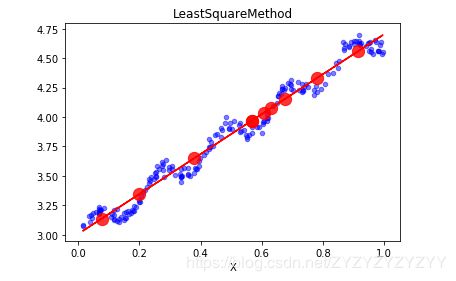
然后，我们在x的范围内再取10个随机数，并进行预测感受一下。

# 生成最小二乘法类
xArr, yArr = loadDataSet('ex0.txt')
ls = LeastSquared()
ls.fit(xArr,yArr) #训练模型
y_predict = ls.predict(xArr) #预测模型

# 在x范围内，随机生成10个新的x值
x_min = np.min(np.array(xArr)[:,1])
x_max = np.max(np.array(xArr)[:,1])
x_random = np.random.uniform(x_min,x_max,[10,1])

x_new = np.c_[np.ones(10),x_random.flatten()]
y_new = ls.predict(x_new)
y_new = y_new.flatten().tolist()[0]
x_new = x_random.flatten().tolist()

# 可视化
n = len(xArr)                                                      
xcord = [];ycord = [];y_hat = []
for i in range(n): 
    xcord.append(xArr[i][1])
    ycord.append(yArr[i])                    
    y_hat.append(y_predict.tolist()[i][0])
fig = plt.figure()
#添加subplot
ax = fig.add_subplot(111)                                            
#绘制样本点
ax.plot(xcord, y_hat, c = 'red')
ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5)                
ax.scatter(x_new,y_new, s=150, c='r', alpha = 0.8)
#绘制title
plt.title('LeastSquareMethod')                                                
plt.xlabel('X')
plt.show()

这时我们看到，生成的10个随机数都在我们的拟合直线上，对应的y值就是我们的预测值。同样的，我们也手撸了梯度下降算法进行的求解过程，二者得到的结果参数几乎相等。二者可视化效果如下所示（可以看到两个拟合直线是重合的，红色和绿色）：

二者所得参数对比如下，其中梯度下降迭代了500次，可以看到参数结果是几乎一样的。

 

#最小二乘法
ls.params
>>matrix([[3.00774324],
         [1.69532264]])

#梯度下降法，迭代500次
gd.params
>>matrix([[3.00758726],
         [1.69562035]])