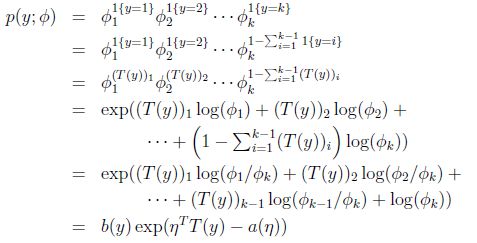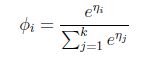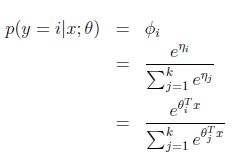机器学习学习笔记（二）——回归

回归（ressgression）

我对回归的认识

在我现在的认识中，回归是找到反映一系列事物的各个特征之间的联系和规律的方法，以充分了解这一系列事物，发现其内部存在的规律，得到回归模型。比如房价预测中房价与面积、地段、楼层等之前的关系，首先对已知的一组房价数据进行研究，建立回归模型，得到回归模型后，再对新数据进行预测。
回归方法的使用流程如下，估计函数h即是回归得到的模型。它可以对输入的数据进行估计预测。

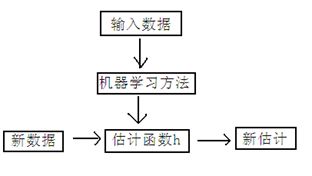
线性回归

线性回归：利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间的关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

线性回归需要满足三个条件：
• 假设结果和数据的特征之间满足线性关系
• 收集的数据中所有的分量都可以看做一个特征数据（有时收集的数据非常大，需要进行数据清洗。这里说的是数据的分量，即数据的一个类别（如房子的单价），而非某一个数据）。
• 每个特征至少对应一个未知的参数
向量表示：

只要找到一组合适的参数，就可以很好的表示出数据满足的模型。也就是说，如果我们将数据的所有特征和结果带入上式，并找到对应的参数，就可以完全地表示出所有的数据来。但这是没有意义的，因为我们本来就已经得到了这些数据的结果。我们找模型只是为了找出这组数据间普遍存在的规律。只是满足样本数据的话，就可能存在欠拟合（样本数据过少）和过拟合（样本数据过多）。因此，我们需要找到合适的拟合参数。具体如下图所示（依次是欠拟合、拟合和过拟合）。

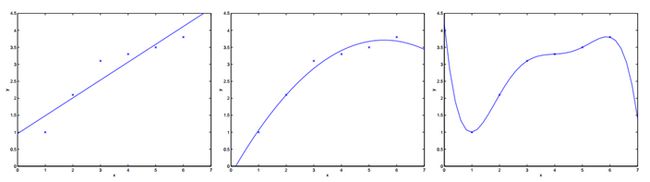
接下来，我们就需要求解刚才的那个公式，找到最适合的参数。因为已知样本中有数据。因此，上式就变成了一个线性矩阵方程，直接求解会很麻烦，现实数据中这样的方程很可能不存在解。因此，换一个思路——求解最接近的解——求与解之间的最小误差。即确定的参数的输出结果能满足既定的误差要求即可。

既然是用误差去评判h函数的参数的好坏，首先需要定义一个误差函数如下：

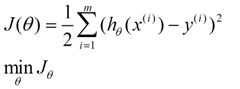
一般这个函数称为损失函数（loss function）或者误差函数(error function)，描述h函数不好的程度。
这个误差函数是用样本数据中的x(i)的估计值与真实值y(i)差的平方和作为误差估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。

为何选用差的平方和？？？
假设根据特征的预测结果与实际结果有误差∈^((i))，那么预测结果θ^T x^((i)) 和真实结果y^((i)) 满足下式：

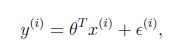
一般来讲，误差满足平均值为0的高斯分布，也就是正态分布。那么x和y的条件概率也就是

对于一组参数θ，输入特征x(i)后结果是y（i）的概率。这样就估计了一条样本的结果概率，然而我们期待的是模型能够在全部样本上预测最准，也就是概率积最大。即每个样本都正确的概率。

上面这个概率积称为最大似然估计。
取最大似然估计的对数函数得：

要使最大似然估计达到最大值，就要使下式达到最小值。

这样用这个式子表示损失函数，既满足误差最小的原则，又满足了最大似然估计的要求。完美！
这就解释了为何误差函数要使用平方和。
当然推导过程中也假定了误差满足高斯分布，但这个假定符合客观规律。

在这个误差函数中，θ是还是唯一的未知量。只要找到一组θ值使误差估计函数最小即可。调整θ以使得J(θ)取得最小值或满足既定误差要求有很多方法，其中有最小二乘法(min square)和梯度下降法（Gradient descent）。

 现在要做的就是确定参数θ，参数确定之后模型就可以使用了。我们希望可以在损失函数然J(θ)最小时确定参数θ。所以接下来的问题就是求J(θ)极小值的问题。上文说到了最小二乘法(min square)和梯度下降法（Gradient descent）。

Ø 梯度下降法
1>首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。（正因为初始点的选取随机，这导致了梯度下降法最大的问题是求得结果有可能是局部极小值，）
 2>改变θ的值，使得J(θ)按梯度下降的方向进行减少。
 梯度方向由J(θ)对θ的偏导数确定:

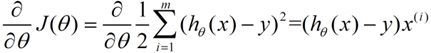
由于求的是极小值，因此梯度方向是偏导数的反方向。结果为

上式中α代表算法速度，下降时，每一步步长的大小，由自己设置。太大可能导致在某一步越过最小值，太小可能导致速度太慢。
迭代更新的方式有两种，一种是批梯度下降，也就是对全部的训练数据求得误差后再对θ进行更新，另外一种是增量梯度下降，每扫描一步都要对θ进行更新。前一种方法能够不断收敛，后一种方法结果可能不断在收敛处徘徊。
一般来说，梯度下降法收敛速度还是比较慢的。
另一种直接计算结果的方法是最小二乘法。
Ø 最小二乘法
将训练特征表示为X矩阵，结果表示成y向量，仍然是线性回归模型，误差函数不变。那么θ可以直接由下面公式得出
令J(θ) = 0得：

因为

所以，对损失函数求导得：

设定损失函数的导数是0，得下式结果。

但此方法要求X是列满秩的，而且求矩阵的逆比较慢。

局部加权回归

局部加权回归就是在损失函数的前提下，为每一个样本加入权值。
基本假设是

其中假设w^((i)) 符合公式

其中x是要预测的特征，这样假设的道理是离x越近的样本权重越大，越远的影响越小。这个公式与高斯分布类似，但不一样，因为w^((i)) 不是随机变量。如下图所示。

图中，τ越小，远处的点的权重下降越快；τ越大远处的点权重下降越慢。
最终的回归结果：

此方法称为非参数学习算法，因为误差函数随着预测值的不同而不同，这样θ无法事先确定，预测一次需要临时计算，每个点的模型都不相同，感觉类似KNN。

logistic回归

线性回归用来解决连续型模型，其回归结果是连续的。而logistic回归则多用来进行分类。
logistic回归本质上还是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0和1上。
对数回归的假设函数如下，线性回归假设函数只是θ^T x。

g(z)为一个sigmoid函数

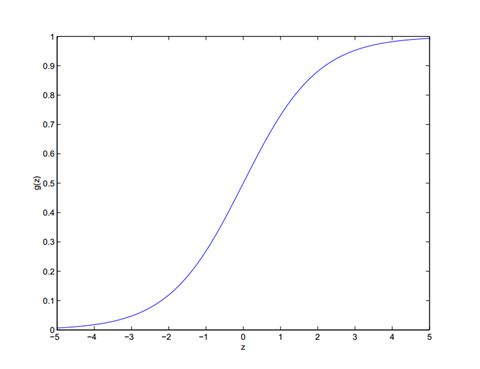
logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是

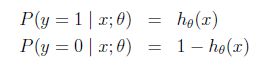
当然假设它满足泊松分布、指数分布等等也可以，只是比较复杂。
这里求的仍然是最大似然估计，不同的是这里没有损失函数。因此直接将最大似然估计取对数后再进行求导，这与对线性回归中对损失函数进行梯度下降的结果是一致的，不同的是θ^T x^((i)) 换成了hθ (x^((i) ))，而hθ (x^((i) ))实际上就是θ^T x^((i)) 经过g(z)映射过来的。得到迭代公式结果如下。

一种快速的求导迭代——牛顿法：

当要求解f(θ)=0时，如果f可导，那么可以通过迭代公式

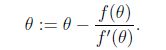
来迭代求解最小值。
当应用于求解最大似然估计的最大值时，变成求解l^′ (θ)=0的问题。
那么迭代公式写作

当θ是向量时，牛顿法可以使用下面式子表示

其中

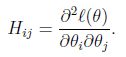
是n×n的Hessian矩阵。
牛顿法收敛速度虽然很快，但求Hessian矩阵的逆的时候比较耗费时间。
牛顿法收敛解析图：

当初始点X0靠近极小值X时，牛顿法的收敛速度是最快的。但是当X0远离极小值时，牛顿法可能不收敛，甚至连下降都保证不了。原因是迭代点Xk+1不一定是目标函数f在牛顿方向上的极小点。

4.softmax回归

一般线性回归
之所以在logistic回归时使用

是由一套理论作支持的。
这个理论便是一般线性模型。
首先，如果一个概率分布可以表示成

时，那么这个概率分布可以称作是指数分布。
伯努利分布，高斯分布，泊松分布，贝塔分布，狄特里特分布都属于指数分布。
在Logistic回归时采用的是伯努利分布，伯努利分布的概率可以表示成

其中

得到
Φ=1/(1+e^η )
这就解释了logistic回归时为了要用这个函数。
一般线性模型的要点是
1.y|x; θ 满足一个以η为参数的指数分布，那么可以求得η的表达式。
2.给定x，我们的目标是要确定T(y)，大多数情况下T(y)=y，那么我们实际上要确定的是h(x)，而h(x)=E[y|x]。（在对数回归中期望值是Φ，因此h是Φ；在线性回归中期望值是μ，而高斯分布中η=μ，因此线性回归中h=θ^T x）。
3.η=θ^T x
Softmax回归
Softmax回归属于一般线性回归的一种，也可以当做是对Logistic回归的扩展，在Logistic回归中，将所有的数据回归成0和1两类，而Softmax回归则将数据回归成0到K若干类。
假设预测值y有k种可能，即y∈{1,2,…,k},比如k=3时，可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。
定义

那么

这样

即式子左边可以有其他的概率表示，因此可以当做是k-1维的问题。
T(y)这时候一组k-1维的向量，不再是y。即T(y)要给出y=i（i从1到k-1）的概率

应用于一般线性模型

那么

最后求得

而y=i时

求得期望值

那么就建立了假设函数，最后就获得了最大似然估计

对该公式可以使用梯度下降或者牛顿法迭代求解。
解决了多值模型建立与预测问题。

总结

线性回归、logistic回归和softmax回归之间有着清楚的脉络联系。对于连续型模型使用线性回归，对于二分类模式使用logistic回归，对于softmax回归则是在logistic回归的基础上扩展到了k个分类。

代码实现（机器学习实战Python代码）：

完整代码：

from numpy import *

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
    labelMat = mat(classLabels).transpose() #convert to NumPy matrix
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat,labelMat=loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0] 
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)   #initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not 
            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():
    frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print "the error rate of this test is: %f" % errorRate
    return errorRate

def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))

完整代码，点击这里

特别感谢

1. 感谢许利杰前辈的邮件，本博客参考了许利杰前辈的资料！非常感谢！！