图解算法学习笔记（四）：快速排序

目录

1） 示例1：

2）快速排序

3) 再谈大O表示法

4）小结

本章内容：学习分而治之，快速排序

1） 示例1：

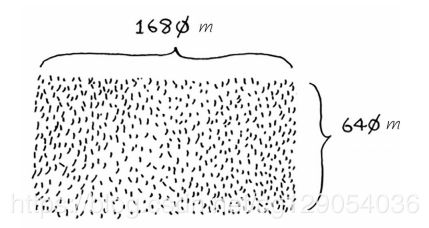
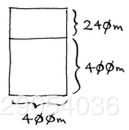
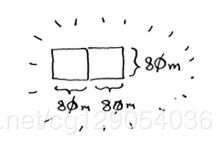
假设你是农场主，有一小块土地，你要将这块地均匀分成方块，且分出的方块尽可能大。如何分？

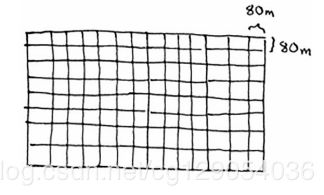
你要将这块地均匀分成方块，且分出的方块要尽可能大。显然，下面的分法不符合要求。

此时，你应该使用D&C策略（divide and conquer）。包括两步骤:

(1) 找出基线条件，这种条件必须尽可能简单。

(2)不断将问题分解（或者说缩小规模），直到符合基线条件。

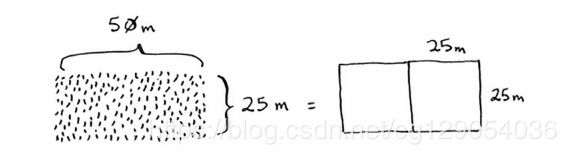
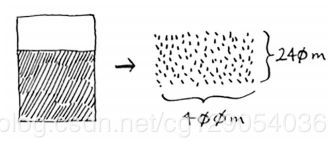
下面就来使用D&C找出问题的解决方案。首先，找出基线条件。最容易处理的情况是，一条边的长度是另一边的整数倍。

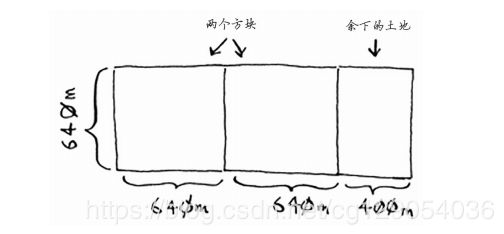
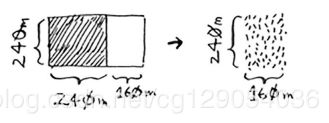
现在找出递归条件，这正是D&C的用武之地。每次递归都必须缩小问题的规模，如何缩小问题的规模呢，首先，找出这块地可容纳的最大方块。

如图，划出了两个方块，同时余下一小块地。现在是顿悟时刻，何不对余下的那一小块地使用相同的算法呢？

这里有一个关键的地方，就是适用于这小快地的最大方块，也是适用于整块地的最大方案。感兴趣的可以查查欧几里得算法。

https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm

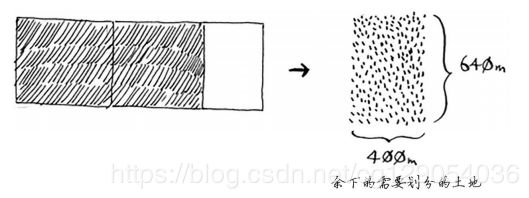
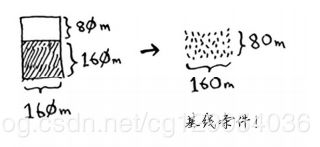
接下来就是使用同样算法。直到余下土地为方块。

           

      

现在我们找到了最大方块，如下图：

2）快速排序

快速排序是一种常用的排序算法，比选择排序快得多，例如，C语言标准库的函数qsort实现的就是快速排序。

对排序算法来说，最简单的数组什么样呢？就是根本不需要排序的数据。

因此，基线条件为数组为空或只包含一个元素。在这种情况，只需返回数组：

def quicksort(array):
    if len(array) < 2:
        return array

我们来看更长的数组。对包含两个元素的数组进行排序也很容易：

包含三个元素呢？

现在介绍快速排序的工作原理：首先，从数组中选择一个元素，这个元素被称为基准值(pivot).

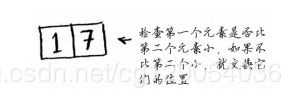
我们暂时将数组的第一个元素用作基准值.接下来，找出比基准值小的元素以及比基准值大的元素。

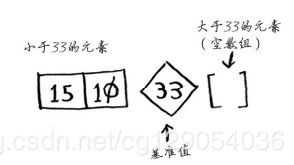
这被称为分区(partitioning)。这里只进行了分区，得到的两个子数组是无序的。如何对子数组进行排序呢？对于包含两个元素的数组以及空数组，快速排序知道如何将它们排序。因此对这两个子数组进行快速排序，再合并结果，就得到一个有序数组！

quicksort([15, 10]) + [33] + quicksort([])
> [10, 15, 33]

现在我们知道了如何对包含三个元素的数组进行排序了：

（1）选准基准值。

（2）将数组分成两个子数组：小于基准值的元素和大于基准值的元素。

（3）对这两个子数组进行快速排序。

下面是快速排序的代码：

def quicksort(array):
    if len(array) < 2:
        return array
    else:
        pivot = array[0]
        less = [i for i in array if i<= pivot]
        greater = [i for in array if i > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)

 

3) 再谈大O表示法

我们再来看看常见的大O运行时间：

这里需要说明的是，在平均情况下，快速排序的运行时间为O(n logn)。

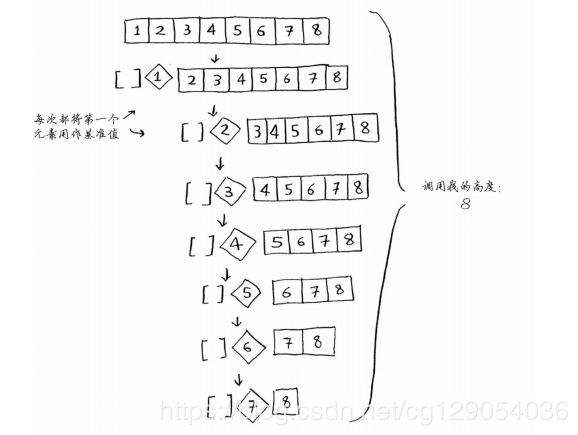
快速排序的性能高度依赖于你选择的基准值。来看下面这样一个有序数组，每次都选择第一个元素为基准值，来看看快速排序过程，

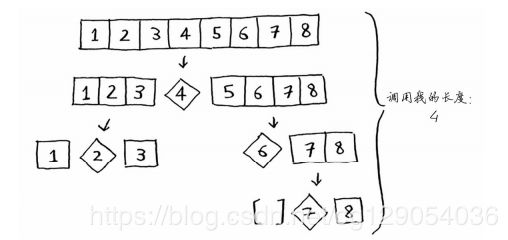
现在选择中间元素作为基准值，看看排序过程：

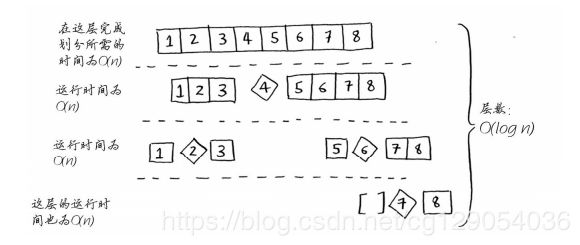
第一个示例展示的是最糟情况，栈长为O(n)，第二个示例展示的是最佳情况，栈长为O(log n)。与此同时，在调用栈的每层都涉及全部8个元素，操作数为O(n)。

现在可以得出快速排序的运行时间为O(n logn)（最佳情况），最佳情况也是平均情况。

4）小结

• D&C将问题逐步分解，使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组；
• 实现快速排序时，请随机选地选择用做基准值的元素，快速排序的平均运行时间为O(n log n);
• 大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在；
• 比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(log n)的速度为O(n)块很多。