机器学习实战(MachineLearinginAction) 第三章 决策树

决策树(decision tree)很流行的一个原因就是对机器学习算法的知识要求很低.

决策模块(decision block)
终止模块(terminating block):表示已经得出结论,可以终止运行
分支(branch)连接决策模块或终止模块.

有点:计算复杂度不高,易于理解,对中间值的缺失不敏感,可处理不相关特征数据.
缺点:可能会产生过度匹配问题.
使用数据类型:数值型和标称型

创建数据集

def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

计算信息熵
信息增益(information gain)
熵(entropy)
如果待分类的事物可能划分在多个分类中,则符号 xi x i 的信息定义为
l(xi)=−log2p(xi) l ( x i ) = − l o g 2 p ( x i ) ,注意这个是信息值
其中 p(xi) p ( x i ) 是选择该分类的概率.
为了计算熵,要计算所有类别所有可能值包含的信息期望值:
H=−∑Ni=0p(xi)log2p(xi) H = − ∑ i = 0 N p ( x i ) l o g 2 p ( x i ) ,这个才是熵
其中n是分类的数目.

信息熵图1

import matplotlib.pyplot as plt
from math import log
x = [i/100 for i in range(1,101)]
y = [-log(i,2) for i in x]
plt.xlabel("p(x)")
plt.ylabel("l(x)")
plt.title("entropy")
plt.plot(x,y)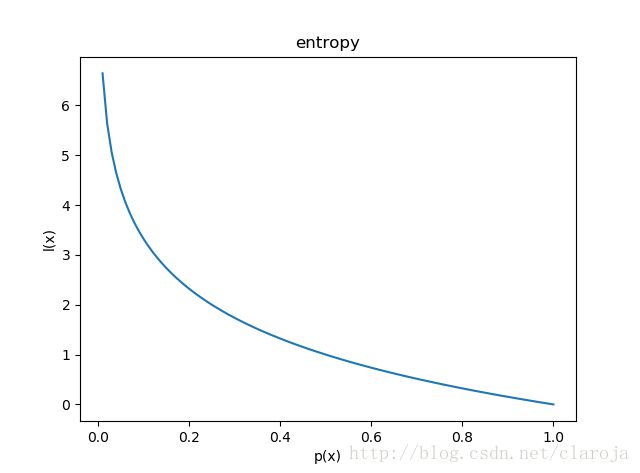

概率越小,信息量越大.比如明天我们这太阳从东边升起,这是概率为1的事情,所以信心量很小.

熵的计算的目标是目标变量,也就是说选择不同的特征,会对应不同的目标变量,而这些不同的目标变量会对应不同的熵

信息熵图2

import matplotlib.pyplot as plt
from math import log
from mpl_toolkits.mplot3d import Axes3D

x = [i/100 for i in range(1,100)] y = [1-i for i in x] z = [-i*log(i,2)-(1-i)*log((1-i),2) for i in x] fig = plt.figure() ax = Axes3D(fig) ax.scatter(x, y, z)

由上图可以看出在目标变量为2个种类时,当二者的出现概率都为0.5时

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)  # 计算数据集的长度
    labelCounts = {}
    for featVec in dataSet: # 计算每个目标变量的出现的次数
        currentLabel = featVec[-1]  # 获得该样本的目标变量
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0  # 计算目标变量出现的次数
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:  # 计算信息熵
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt

熵越高,则混合的数据也越多.

按照给定特征划分数据集

def splitDataSet(dataSet, axis, value):
    """ 分割数据集,去掉指定的axis :param dataSet: (list)数据集 :param axis: (int)要去掉的列 :param value: (int)在axis列符合条件的值 :return: 切割之后的数据集 """
    retDataSet = []  # 创建新的列表,是为了不破坏原有的列表,因为list类型是引用类型
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #截取该行之前的
            reducedFeatVec.extend(featVec[axis+1:])  # 添加该行之后的
            retDataSet.append(reducedFeatVec)
    return retDataSet

计算信息增益最大的的特征

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1  # 计算特征的个数,最后一列是类别标签
    baseEntropy = calcShannonEnt(dataSet)  # 计算熵的期望,这里使用的目标变量
    bestInfoGain = 0.0; bestFeature = -1  # 初始化最优信息增益,初始化最优特征
    for i in range(numFeatures):  # 迭代特征
        featList = [example[i] for example in dataSet]  # 创建所有样本的第i个特征的列表
        uniqueVals = set(featList)  # 去重
        newEntropy = 0.0  # 初始化熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)  # 获取分割之后的数据集
            prob = len(subDataSet)/float(len(dataSet))  # 获取该特征值的概率
            newEntropy += prob * calcShannonEnt(subDataSet)  # 计算该值的信息熵
        infoGain = baseEntropy - newEntropy # 计算信息增益
        if (infoGain > bestInfoGain):       # 如果信息增益大于最优增益
            bestInfoGain = infoGain         # 更新
            bestFeature = i
    return bestFeature                      # 返回信息增益最大的特征

创建树

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    """ 递归创建树 :param dataSet: (list)嵌套列表,数据集 :param labels: (list)标签列表 :return: (dict)返回嵌套字典 """
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]  # 当所有特征都相同的时候,停止
    if len(dataSet[0]) == 1:  # 当遍历完所有特征之后停止
        return majorityCnt(classList)  # 遍历特征之后如果特征值还不唯一,则通过计数的方法确定哪个是最终特征
    bestFeat = chooseBestFeatureToSplit(dataSet)  # 获取最优特征
    bestFeatLabel = labels[bestFeat]  # 获取特征对应的标签
    myTree = {bestFeatLabel:{}}  # 
    del(labels[bestFeat])  # 删除已经使用的标签
    featValues = [example[bestFeat] for example in dataSet]  # 获取样本最优特征,组成列表
    uniqueVals = set(featValues)  # 去重
    for value in uniqueVals:
        subLabels = labels[:]  # 复制所有剩余的labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree

叶节点(leaf node)
判断节点(decision node)

决策树分类器
就是查询嵌套词典

def classify(inputTree,featLabels,testVec):
    """ 决策树模型分类器 :param inputTree: (dict)一个嵌套字典,树模型 :param featLabels: (list)特征标签 :param testVec: (list)测试向量 :return: """
    firstStr = inputTree.keys()[0]  # 获得第一个节点key
    secondDict = inputTree[firstStr]  #
    featIndex = featLabels.index(firstStr)
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): # 如果是字典就继续递归,如果不是则返回
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel