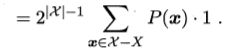周志华西瓜书《机器学习笔记》学习笔记第一章《绪论》
最近在帮学弟做一个关于OCR的项目,所以这几个星期都没有在CSDN上更新文章。今天登录后发现有还几个小伙伴关注我了,很开心~。我会继续在CSDN上更新一些内容,总结自己每个阶段的学习情况。
周志华老师的西瓜书堪称学习机器学习的必备书籍,很多学生包括我自己都是从这本书开始接触机器学习。周志华老师将这本书定位一本自学用书和科研参考书,但对于初学者来说,在学这本书的时候肯定有很多不明白的地方。我大概在去年的十月份开始接触这本书,当时学业压力比较大,只是大体上对这本书进行翻阅,没有深入思考,以至于现在对这本书的理解还是非常浅薄。为此我进行本系列文章的写作,一遍学一遍总结,我会尽自己最大的努力去推导书中的公式。
当然,我写的这些文章肯定也存在一些认识不够到位的地方,希望可以和大家多交流。谨以此作为自己学习的总结,并作为一个和大家进行交流的平台。
本章是全书的第一章,作者在这一章节主要介绍了一些机器学习中常用的概念和原理,并总结回顾机器学习的发展历程,气提纲挈领的作用,总体来说这一部分难度并不大。
1.1 引言
这一部分主要讲解了什么是机器学习,周志华老师在这里举了很多例子来帮助我们进行理解。
1、经验: 在生活中,我们存在很多用经验来做判断的事情,比如挑西瓜、用生活常识来判断明天的天气等,在计算机系统中,这些经验用"数据”来进行表示,一条数据就是一个经验。
2、机器学习的任务: 关于计算机从数据中产生“模型”的算法,也就是我们经常说的学习算法。有了这个模型,我们就可以将数据输入其中从而得到判断结果。
3、机器学习的形式化定义: 假设用P来评估计算机程序在某一个任务类T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们就说关于T和P,该程序对E进行了学习。
1.2 基本术语
这里是对一些基本术语的介绍:
1、属性: 反映事件或对象在某方向的表现或性质,也称为特征。如西瓜的“色泽”、“敲声”等。
2、属性值: 顾名思义,属性的取值就称为属性值,如“青绿”、“乌黑”等。
3、属性空间: 属性张成的空间称为属性空间,也称为样本空间或者“输入空间”。如把“色泽”、“根蒂”、“敲声”作为三个坐标轴,则他们张成一个描述西瓜的三维空间,每个西瓜都可以在这个空间中找到自己的坐标位置。由于空间中每个点都对应一个坐标向量,所以我们也在一个实例称为一个“特征向量”。
4、数据集: 一组记录的集合称为数据集。
5、样本: 其中每一条记录是关于一个事件或对象的描述,称为示例或样本,例如:(色泽=青绿;根蒂=稍蜷;敲声=沉闷)
6、学习: 从数据中学得模型的过程称为学习,这个过程一般通过执行某个学习算法来完成,也称为训练。
7、训练数据: 训练过程中使用的数据称为训练数据。
8、训练样本: 训练过程的每个样本称为训练样本。
9、训练集: 由训练样本组成的集合称为训练集。
10、假设: 学得模型对应了关于数据的某种潜在的规律,即hypothesis,这个英文名我们会在后续文章中继续用到。
11、学习器: 其实学习的过程是为了找出或者逼近真相,所以我们有时候也把模型称为“学习器”,可看作学习算法在给定数据和参数空间上的实例化。
12、标记(label): 想要学得一个模型,仅有已有的示例数据是不够的。要建立一个关于预测的模型,需要获得训练样本的“结果”信息。例如“((色泽=青绿;根蒂=稍蜷;敲声=浊响),好瓜)”。这里关于示例结果的信息“好瓜”,就称为标记。
13、分类: 如果我们预测的值是离散值,如“好瓜”、“坏瓜”,这一类学习任务就称为分类。
14、回归: 如果我们预测的值是连续值,例如西瓜的成熟度0.95,0.37,则我们称此类学习任务为回归。
15、监督学习(supervised learning): 训练的数据既有特征又有标签(,通过训练,典型代表是分类和回归。
16、无监督学习(unsupervised learning): 训练的数据没有标签存在,通过数据之间的内在联系和相似性将他们分成若干类。典型代表为聚类。
17、泛化能力: 我们学的模型可以适用于新样本的能力称为泛化能力,具有强泛化能力的模型可以很好的适用于整个样本空间。
18、独立同分布: 假设样本空间中全体样本服从一个未知的“分布”D,我们获得的每个样本都是独地从这个分布上采样获得的,即“独立同分布”。
1.3 假设空间
归纳(induction)和演绎(deduction)是科学推理的两大基本手段。
- 归纳(induction): 从特殊到一般的“泛化”过程。即从具体的事实归结出一般性规律
- 演绎(deduction): 从一般到特殊的“特化”(specialization)过程。即从基础原理推演出具体的情况
归纳学习有狭义和广义之分,广义的归纳学习大体相当于从样例中进行学习,而狭义的归纳学习则要求从训练数据中学得概念,因此也称为"概念学习"或者“概念生成”。
概念学习中最基本是“布尔概念学习”,即对“是”、“不是”主要可以表示为0/1的布尔值的目标概念的学习。
我们可以把学习过程看做是一个在所有的假设(hypothesis)组成的空间中进行搜索的空间,搜索目标是找到与训练集“匹配”(fit)的假设,即能够将训练集中的瓜判断正确的假设。假设一旦确定,假设空间及其规模大小就确定了。
我们以西瓜问题的假设空间为例来对这一部分进行说明:西瓜的色泽、根蒂和浅白均有三个可能的取值,除此以外,还有一个取任何值均合适的参数“ * ",所以我们面临的假设空间规模大小为 4 × 4 × 4 + 1 = 65 4\times4\times4+1=65 4×4×4+1=65
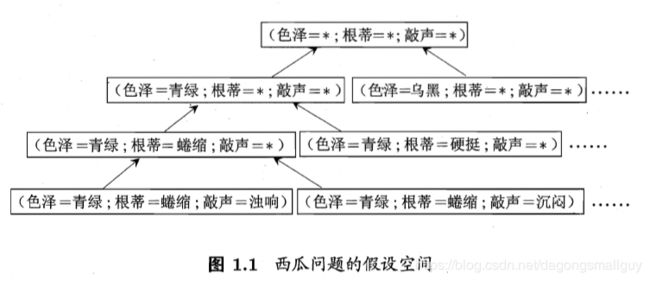
我们可以有很多策略对这个假设空间进行搜索,例如自顶向下,从一般到特殊,或是自底向上,从特殊到一般,搜索过程中可以不用不断删除与正例不一致的假设,和与反例一致的假设,最红将会得到与训练集一致(即对所有的训练样本能够进行正确判断)的假设,这就是我们学的得的结果。
在现实问题中,我们有时候会面临很大的假设空间,但是学习过程是基于有限样本集进行的。因此可能有多个假设与训练集一致,即存在着一个与训练集一致的“假设集合”,我们称之为“版本空间”。
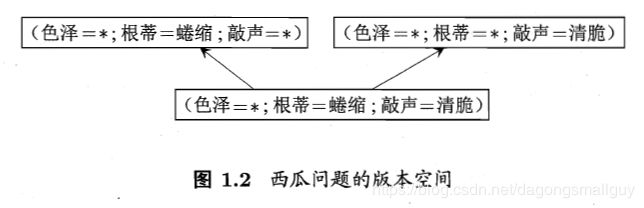
1.4 归纳偏好
通过学习得到的模型可以对应假设空间中的一个假设。但是上文版本空间的有关知识告诉我们,当存在多个假设时,不同的假设有不同的输出,这显然不符合我们的期望。
我们把机器学习算法在学习过程中对某种类型的偏好就称为“归纳偏好”,或者简称为“偏好”。任何一个有效的机器学习算法都必须要有偏好,否则会被假设空间中的看似在训练集中“等效”的假设所迷惑从,从而产生无法确定的结果。
归纳偏好对应了学习计算法本身所作的关于“什么样的模型更好的假设”,在具体的现实问题中,这个假设是否成立。即算法的归纳偏好是否与问题本身匹配,大多数情况下直接决定了算法能否取的很好的性能。
“奥卡姆剃刀”为我们提供了一种常用的,自然科学研究种最基本的法则,可以用来引导算法确立“正确”的偏好。即“若有多个假设与观察一致,则选择最简单的那个”。
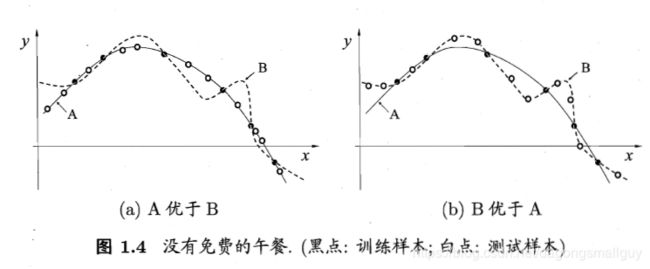
根据“奥卡姆剃刀”法则,对于如下两个算法A和B,我们根据平滑曲线的某种“描述简单性”希望算法A的性能比算法B更好。左图的结果显示:与B相比,A与训练集外的样本更一致,换言之,A的泛化能力比B强。但是右图的结果显示算法B的性能更好,这种情况也有可能出现。
接下来,我们用简单的数学公式对以上理论进行说明。
我们假设样本空间 χ \chi χ和假设空间 H H H都是离散的,令 P ( h ∣ X , ε a ) P\left ( h|X,\varepsilon _{a} \right ) P(h∣X,εa)代表算法 ε a \varepsilon _{a} εa基于训练数据 X X X产生假设 h h h的概率,再令 f f f代表我们希望学习的真实函数。
则 ε a \varepsilon _{a} εa的“训练集外误差”,即 ε a \varepsilon _{a} εa在训练集外的所有样本上的误差为:

在这个公式中, P ( x ) P(x) P(x)为函数 x x x本身的概率,我们用指示函数选出与真实函数不同的那一部分,然后将其乘以h相应的概率,因为在这里我们提出的h不止一个,我们需要对所有的h的误差进行求和。
对于二分类问题,当它的真实函数可以是任何函数 χ \chi χ都在0到1之间时,我们对所有可能的f按均匀分布对误差求和,有: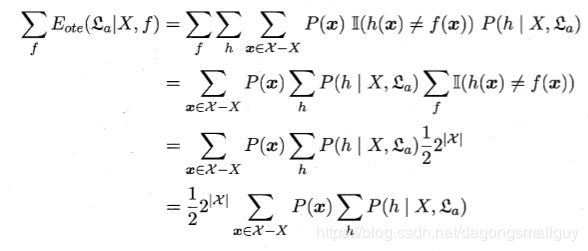
对于上式我们需要做如下解释,若 f f f均匀分布,则我们有一般的 f f f对 x x x的预测与 h h h不一致。所以在二分类问题中,当样本数为 χ \chi χ时,我们有 2 ∣ χ ∣ 2^{\left | \chi \right |} 2∣χ∣个对 f f f的预测,其中一半不符合,所以我们有:
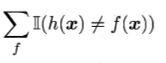
等于 1 2 × 2 ∣ χ ∣ \frac{1}{2}\times 2^{\left | \chi \right |} 21×2∣χ∣
我们从这个式子里面发现似乎总误差与具体选择哪个学习算法无关, 这与我们的生活常识产生矛盾。无论一个算法多么笨拙,无论一个算法多么聪明,他们的期望性能相同,这个就是我们常说的“没有免费的午餐”定理。
但是在推导出这个结果之前,我们假设 f f fd均匀分布,所有问题的出现机会都相同,或者所有的问题都同等重要,这与我们的事实发生矛盾。
NFL定理其实最想告诉我们的,是脱离具体的问题空谈什么算法最好毫无意义,考虑所有的潜在问题,则所有的学习算法都一样好,要谈论具体算法的好坏,必须要引入具体的问题。
1.5 发展历程
20世纪80年代,“从样例中学习”的一大主流师符号主义学习,其代表包括决策树和基于逻辑学习。
20世纪90年代中期之前,“从样例中学习”的另一主流技术是基于神经网络的连接主义学习。
20世纪90年代中期, “统计学习(statistical learning)”闪亮登场并迅速占据主流舞台,代表技术是支持向量机(Support Vector Machine,简称SVM)以及更一般的“核方法”(kernel methods)
21世纪初,连接主义卷土重来,掀起了以“深度学习”为名的热潮。深度学习的前身是连接主义学习