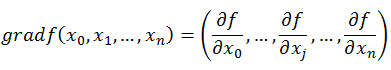机器学习——单层前馈神经网络与BP算法

以下内容均为个人理解，如有错误，欢迎指出

什么是人工神经网络

摘自维基百科¹

人工神经网络（英语：Artificial Neural Network，ANN），简称神经网络（Neural Network，NN）或类神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统，通俗的讲就是具备学习功能。现代神经网络是一种非线性统计性数据建模工具。

由此可知，人工神经网络是一个非线性模型，依网络架构，神经网络的分类主要有：

• 前馈神经网络（Feed Forward Network）
• 递归神经网络（Recurrent Network）
• 强化式架构（Reinforcement Network）

本文介绍BP算法在前馈神经网络的应用

M-P神经元模型

以下关于生物神经元工作方式的描述糅合了周志华老师的《机器学习》^[3]以及一些生物学知识

在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向连着连接的神经元发送化学物质，从而改变这些神经元内的电位，如果某个神经元的电位超过一个阈值时，便会转变为“兴奋”状态，向其他神经元发送化学物质，两个神经元信号的传递方向是单向的

从人工神经网络的概念可知其模仿了生物神经网络，而经典的M-P神经元模型便模仿了上述生物神经元的工作方式：

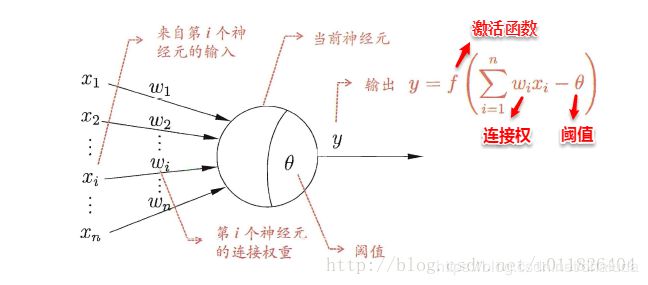
其中，$x_i$可理解为第i个相邻神经元向本神经元发送的化学物质量，$w_i$可理解为单位化学物质对于当前神经元电位的影响，则$w_i{x}_i$表示第i个神经元对本神经元电位的影响（增加or减少多少），假设当前神经元的电位原本为0，则${\sum }_1^n{w}_i{x}_i$表示当前神经元的电位，将其与阈值相减，若大于0，则神经元处于兴奋状态，用激活函数表示本神经元向下一个神经元发送的化学物质数量

单层前馈神经网络

将上述的多个M-P神经元模型按层连接，就能得到单层前馈神经网络，如下：

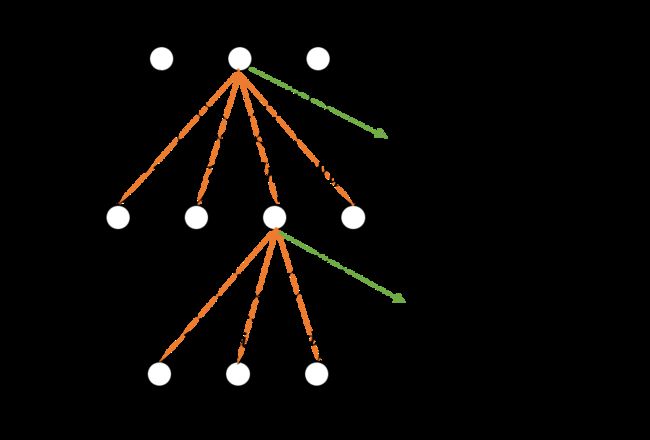
单隐层前馈神经网络由输入层、隐含层、输出层组成，其可简单模拟生物神经网络，每层神经元与下一层神经元连接，神经元之间不存在跨层连接、同层连接，输入层用于数据的输入，隐含层与输出层神经元对数据进行加工

常用的激活函数以及优缺点

我们用激活函数表示本神经元向下一个神经元发送的化学物质数量，科学家经过多年的实验，具有较好结果的激活函数如下

sigmoid函数

• 数学形式
  
  $y=\frac{1}{1+e^{-x}}$
  
  定义域$(-\infty ,+\infty )$，值域$(0,1)$

• 图像
  

• 缺点
  1、指数运算会耗费大量计算资源
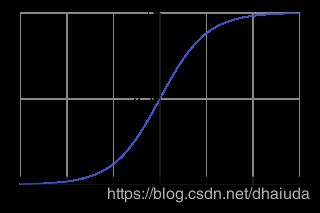
  2、容易出现梯度消失现象（使用batch GD或是mini-batch GD或是SGD），这是由sigmoid的导数图像决定的：
  
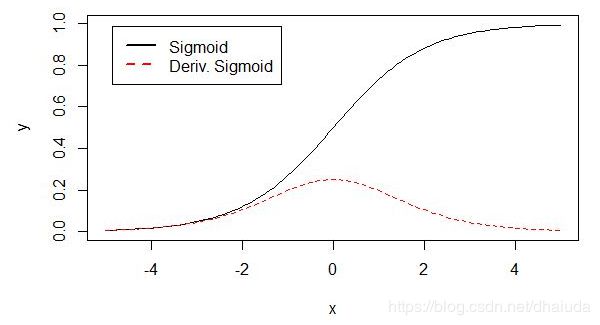
  虚线表示sigmoid的导数，可以看到其很快便趋近于0，这意味着某些权重的更新速度缓慢（使用batch GD或是mini-batch GD或是SGD），神经网络的收敛速度很慢。
  3、其不是零均值，这导致神经网络的收敛速度缓慢，关于这点，网络上大部分解释是这样的：
  
  这个观点我并不认同（也可能是我理解错了），下面的Tanh函数是零均值的，但是它仍然会出现上图所说的情况，假设我们使用Tanh函数作为激活函数，依据链式法则，$\sigma ({\sum }_i{w}_i{x}_i+b)$对$w_i$求导得：${\sigma }^{,}({\sum }_i{w}_i{x}_i+b)x_i$，${\sigma }^{,}({\sum }_i{w}_i{x}_i+b)$恒大于0，当$x_i$一直为正时，对$w_i$的更新也总是正值，个人比较认同的观点是零均值的函数在用SGD进行更新时，效果更接近自然梯度，而sigmoid函数不是零均值，神经网络的收敛速度缓慢

Tanh函数

• 数学形式：
  
  $tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
  
  定义域$(-\infty ,+\infty )$，值域$(0,1)$

• 图像
  

Tanh函数为sigmoid函数变换得到，它是0均值的

• 相比于sigmoid函数，其具有以下优点(摘自深度学习中的激活函数与梯度消失、梯度爆炸)

与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好。文献 [LeCun, Y., et al., Backpropagation applied to handwritten zip code recognition. Neural computation, 1989. 1(4): p. 541-551.] 中提到tanh 网络的收敛速度要比sigmoid快，因为tanh 的输出均值比 sigmoid 更接近 0，SGD会更接近 natural gradient[4]（一种二次优化技术），从而降低所需的迭代次数
关于自然梯度，请查看自然梯度

• 缺点
  1、由导数图像可知，其仍然存在梯度消失现象
  2、设计到指数运算，比较耗时

ReLU函数

• 数学形式
  
  $\text{ReLU}=\max (0,x)$
  
  定义域$(-\infty ,+\infty )$，值域$[0,+\infty )$
  
  
• 图像
  
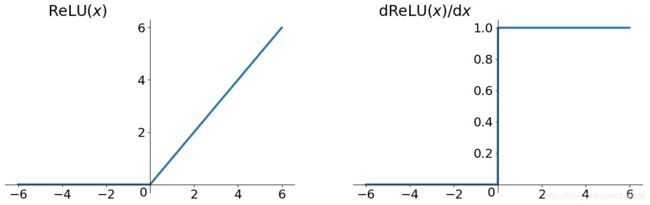
• 优点
  1、在正区间解决了梯度消失问题
  2、计算速度快，一次判断，就会有输出，不需要指数运算等
  3、收敛速度比sigmoid、tanh快
  实战中建议使用该函数
• 缺点
  1、不是零均值
  2、当某次梯度更新比较剧烈时，可能会导致ReLU函数的自变量持续小于0，此时ReLU的输出持续为0，神经元无法激活（死亡），对应的参数不会被更新，由于这个特性，ReLU函数训练后的神经网络具有稀疏性，部分神经元不会被激活。

ReLU的表现如此优异，我觉得一部分原因是因为它较好的模拟了人体神经元工作的场景，2001年，Dayan、Abott从生物学角度模拟出了脑神经元接受信号更精确的激活模型，如下图：

其中横轴是时间(ms)，纵轴是神经元的放电速率(Firing Rate)。同年，Attwell等神经科学家通过研究大脑的能量消耗过程，推测神经元的工作方式具有稀疏性和分布性；2003年Lennie等神经科学家估测大脑同时被激活的神经元只有1~4%，这进一步表明了神经元的工作稀疏性，而经过ReLU训练的神经网络也具有一定的稀疏性

为什么要使用激活函数

如果不使用激活函数，神经网络将会是一个线性模型，线性模型在多数情况下会有局限性，激活函数相当于在神经网络中加入了非线性因素，使神经网络变为非线性模型，更多请查看神经网络激励函数的作用是什么？有没有形象的解释？

神经网络的学习过程

以下摘自周志华老师的《机器学习》

神经网络的学习过程，就是根据训练数据来调整神经元之间的连接权（即单隐层神经网络那张图中的$w_{1j}、w_{2j}$等）以及每个功能神经元的阈值

如何更新神经元之间的连接权与阈值

使用BP算法更新神经元之间的连接权

什么是BP算法

摘自⁴维基百科

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。
反向传播要求有对每个输入值想得到的已知输出，来计算损失函数梯度。因此，它通常被认为是一种监督式学习方法，虽然它也用在一些无监督网络（如自动编码器）中。它是多层前馈网络的Delta规则的推广，可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元（或“节点”）的激励函数可微。

BP算法具有两个关键点：
1、根据输入值获得输出值，计算损失函数的梯度
2、将梯度反馈给最优化算法（例如梯度下降法），由最优化算法对连接权和阈值进行更新，使得损失函数变小

什么是梯度下降算法

首先了解下什么是方向导数

方向导数

• 概念：表示函数沿任意一个方向的变化率，变化率越大，函数沿这个方向增加的越快，它是一个标量
• 个人理解：

1、变化率即函数自变量沿某一方向变化时，因变量变化的快慢，方向导数的式子如下：

这个式子为什么可以反映函数自变量沿某一方向变化时，因变量变化的快慢？
以三维空间为例子（高纬空间也是一样的，只是不好想象），函数Z=f（x，y），A（x₀，y₀，z₀）、B（x₀+$\Delta$x₀，y₀+$\Delta$y₀，z₀+$\Delta$z₀）为Z上的两个点，以（$\Delta$x₀，$\Delta$y₀）方向做垂直于xOy平面的平面，记为H，H平面切割函数Z，会在平面H上留下一个轨迹，这个过程就是将函数Z投影到H平面，在H平面上建立坐标轴，A点记为 （$x_a,y_a$） ，B点为（$x_b,y_b$），则H平面上过 A^’、B^’ 点的直线的斜率为:

当A^’ 与 B^’ 之间的距离趋近于0（即$\rho$趋近于0），方向导数即为 A^’ 点的斜率，斜率可以反映一个函数的”陡峭“程度，即变化率，所以方向导数可以表示函数自变量沿某一方向（在本例中，为（$\Delta$x₀，$\Delta$y₀）方向）变化时，因变量变化的快慢

梯度

• 概念：方向导数取最大值的方向。在当前点，函数沿这个方向的增大速度最快
• 注意事项：梯度是一个向量，方向导数是一个实值

梯度的计算公式：

这个公式的推导不在此处讲解

我们认为梯度的反方向是当前点函数下降速度最快的方向，原因如下²：
对于函数$f(x)$来说，对$f(x+v)$在x处进行泰勒一阶展开得：$f(x+v)\approx f(x)+\nabla f(x{)}^{T}v$，$\nabla$表示梯度，梯度和$v$均为一个向量，$\nabla f(x{)}^{T}v$表示这两个向量的点积，我们想令函数下降的幅度最大，即令$\nabla f(x{)}^{T}v$具有最小值，当两个向量方向相反时，向量点积具有最小值，此时$\nabla f(x{)}^T$与$v$方向相反，所以梯度的反方向，是函数在当前点下降速度最快的方向，由此可导出梯度下降的公式，假设待优化参数$x$为$(x_1,x_2,....,x_n)$，则参数的更新公式如下：

$x_1=x_1-\eta \frac{\partial f(x)}{\partial x_1}$
$x_2=x_2-\eta \frac{\partial f(x)}{\partial x_2}$
…
$x_n=x_n-\eta \frac{\partial f(x)}{\partial x_n}$

其中$\eta$表示往梯度反方向前进的“步数”，“步数”过小会导致函数收敛速度过慢，过大会导致函数震荡不收敛

在单层前馈神经网络中使用BP算法

本节将基于下列条件推导参数的更新表达式

• $f(x)$表示sigmoid激活函数
• 对于训练样例（$x_k,y_k$）,单层前馈神经网络的输出为$\widehat{y_k}=(\widehat{y_1^k},\widehat{y_2^k},....,\widehat{y_l^k})$，即$\widehat{y_j^k}=f({\beta }_j-{\theta }_j)$，${\theta }_j$表示输出层第$j$个神经元的阈值，${\beta }_j$为输出层第$j$个神经元的输入，${\beta }_j={\sum }_{h=1}^q{w}_{hj}{b}_h$，$b_h$表示第h个隐含层神经元的输出，$w_{hj}$表示隐含层第$h$个神经元与输出层第$j$个神经元的连接权
• $b_h=f({\alpha }_h-{\gamma }_h)$，${\alpha }_h$表示第$h$个隐含层神经元的输入,${\alpha }_h={\sum }_{i=1}^d{v}_{ih}{x}_i$，$v_{ih}$表示输入层第$i$个神经元与隐含层第$h$个神经元的连接权，${\gamma }_h$表示隐含层第$h$个神经元的阈值
• 我们使用均方误差度量神经网络的输出$\widehat{y_j^k}$与训练样例的实例$y_k$的差距：$E_k=\frac{1}{2}{\sum }_{j=1}^l(\widehat{y_j^k}-y_j{)}^2$，这就是损失函数。使用梯度下降法更新连接权，使均方误差（损失函数）不断下降，我们先推导针对单个样例，单层前馈神经网络如何利用BP算法更新神经元的连接权

我们需要优化的参数（忽略了下标）有：$w、\theta 、\gamma 、v$，我们首先将训练数据（$x_k,y_k$）输入到单层前馈神经网络中，获得输出值后使用BP算法更新参数

针对sigmoid激活函数的推导过程

首先明确一点，sigmoid函数具有一个很好的性质，其一阶导数为$f(x)(1-f(x))$。我们随机初始化（也可以按条件初始化）所有待优化参数的值，先将训练样例输入到单层前馈神经网络，获得待优化参数（忽略下标）$w、\theta 、\gamma 、v$的值

1、对$w_{hj}$进行更新

运用求导的链式法则可得：$\frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \widehat{y_j^k}}\ast \frac{\partial \widehat{y_j^k}}{\partial {\beta }_j}\ast \frac{\partial {\beta }_j}{\partial w_{hj}}$，则有$g_j^k=\frac{\partial E_k}{\partial \widehat{y_j^k}}\ast \frac{\partial \widehat{y_k^k}}{\partial {\beta }_j}={\hat{y}}_j^k(1-{\hat{y}}_j^k)({\hat{y}}_j^k-y_j^k)$，设$w_{hj}$更新后为$w_{hj}^{\prime }$，则有$w_{hj}^{\prime }=w_{hj}-\eta g_j^k{b}_h$

2、对${\theta }_j$进行更新

运用求导的链式法则可得：$\frac{\partial E_k}{\partial {\theta }_j}=\frac{\partial E_k}{\partial \widehat{y_j^k}}\ast \frac{\partial \widehat{y_j^k}}{\partial {\theta }_j}={\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)$，设${\theta }_j$更新后为${\theta }_j^{\prime }$，则有${\theta }_j^{\prime }={\theta }_j-\eta (-g_j^k)$

3、对${\gamma }_h$进行更新

注意到${\gamma }_h$会影响到$(y_1,y_2,....,y_n)$，我们将均方误差展开：

$E_k=\frac{1}{2}[({\hat{y}}_1-y_1{)}^2+({\hat{y}}_2-y_2{)}^2+.....+({\hat{y}}_n-y_n{)}^2]$

假设我们对${\gamma }_1$进行更新，注意到：

${\hat{y}}_i=f({\beta }_i-{\theta }_i)=f({\sum }_{h=1}^q(w_{hi}{b}_h)-{\theta }_i)(i=1,2....,n)$

$b_1=f({\alpha }_1-{\gamma }_1)$

所以对${\gamma }_h$求导会是一个和式:

$\frac{\partial E_k}{\partial {\gamma }_h}=-{\sum }_{j=1}^l({\hat{y}}_j^k-y_j^k){\hat{y}}_j^k(1-{\hat{y}}_j^k)w_{hj}{b}_h(1-b_h)$

设$e_h^k=-{\sum }_{j=1}^l({\hat{y}}_j^k-y_j^k){\hat{y}}_j^k(1-{\hat{y}}_j^k)w_{hj}{b}_h(1-b_h)$

设${\gamma }_h$更新后为${\gamma }_h^{\prime }$，则有${\gamma }_h^{\prime }={\gamma }_h-\eta e_h^k$

4、对$v_{ih}$进行更新

注意到$v_{ih}$会影响到$(y_1,y_2,....,y_n)$，我们将均方误差展开：

$E_k=\frac{1}{2}[({\hat{y}}_1-y_1{)}^2+({\hat{y}}_2-y_2{)}^2+.....+({\hat{y}}_n-y_n{)}^2]$

假设我们对$v_{11}$进行更新，注意到：

${\hat{y}}_i=f({\beta }_i-{\theta }_i)=f({\sum }_{h=1}^q(w_{hi}{b}_h)-{\theta }_i)(i=1,2....,n)$

$b_1=f({\alpha }_1-{\gamma }_1)$

${\alpha }_1={\sum }_{i=1}^d{v}_{i1}{x}_i$

所以对$v_{ih}$求导会是一个和式:

$\frac{\partial E_k}{\partial v_{ih}}={\sum }_{j=1}^l({\hat{y}}_j^k-y_j^k){\hat{y}}_j^k(1-{\hat{y}}_j^k)w_{hj}{b}_h(1-b_h)x_i$

设$v_{ih}$更新后为$v_{ih}^{\prime }$，则有$v_{ih}^{\prime }=v_{ih}-\eta (-e_h^k)x_i$

上述过程是对于单个样例进行推导，假设有m个训练样例，我们需要最小化的是训练集上的累积误差：$E=\frac{1}{m}{\sum }_{k=1}^m{E}_k$，则参数更新公式变为：

$w_{hj}^{\prime }=w_{hj}-\eta \frac{1}{m}{\sum }_{k=1}^m{g}_j^k{b}_h$

${\theta }_j^{\prime }={\theta }_j-\eta \frac{1}{m}{\sum }_{k=1}^m(-g_j^k)$

${\gamma }_h^{\prime }={\gamma }_h-\eta \frac{1}{m}{\sum }_{k=1}^m{e}_h^k$

$v_{ih}^{\prime }=v_{ih}-\eta \frac{1}{m}{\sum }_{k=1}^m(-e_h^k)x_i$

在平常的训练中，训练数据通常非常庞大，我们需要完全读取完训练数据后才能更新参数，这会导致参数的更新速度非常缓慢，因此，我们通常使用SGD或是mini-batch GD进行参数的更新

SGD

概念：每次读取一个训练数据，对参数进行更新
缺点：不同训练样例的更新效果可能会出现抵消现象，但是随机梯度下降法被证明是收敛的

mini-batch GD

概念：读取部分训练数据，运用累计误差对参数进行更新
实践中通常采用mini-batch GD，mini-batch GD也是收敛的

为什么mini-batch GD、SGD是收敛的

本人比较认同以下观点，内容摘自知乎⁵

直观来看，batch GD, mini-batch GD, SGD都可以看成SGD的范畴。因为大家都是在一个真实的分布中得到的样本，对于分布的拟合都是近似的。那这个时候三种方式的梯度下降就都是可以看成用样本来近似分布的过程，都是可以收敛的！

全局最小与局部最小

上述更新过程在梯度为0时便不会在更新参数，但是梯度为0时可能是全局最小点，也可能是局部最小点，我们当然希望我们的模型收敛于累计误差的全局最小点，但有时我们的模型会收敛于局部最小点，为此，我们可以使用某些启发式的方法尝试跳出局部最小点，但不一定能获得全局最小
1、模拟退火算法
2、遗传算法
3、用多组不同参数初始化神经网络，获得误差最小的一组参数作为最终方案
4、使用SGD或mini-batch GD，由于其不是对全局累积误差进行更新，有些样例对参数的更新效果会使全局累计误差往局部最小的方向走，有些样例对参数的更新效果可能使全局累计误差跳出局部最小

正则化

由于神经网络的学习能力很强大，有可能过于好的拟合训练数据，从而失去泛化能力（即对于训练数据的误差不断下降，但是测试数据的误差不断上升），为了防止过拟合的出现，我们通常对累积误差进行正则化，让累积误差加上一个用于描述网络复杂度的部分，即$E=\lambda \frac{1}{m}{\sum }_{k=1}^m{E}_k+(1-\lambda ){\sum }_i{w}_i^2$，$\lambda ϵ(0,1)$，可通过调参进行确定

参考文献

[1] 人工神经网络
[2] 为什么梯度的负方向是局部下降最快的方向?
[3] 《机器学习》 周志华
[4] BP算法
[5] 如何理解随机梯度下降(Stochastic gradient descent，SGD)？