生成对抗网络(GAN)应用于图像分类
近年来,深度学习技术被广泛应用于各类数据处理任务中,比如图像、语音和文本。而生成对抗网络(GAN)和强化学习(RL)已经成为了深度学习框架中的两颗“明珠”。强化学习主要用于决策问题,主要的应用就是游戏,比如deepmind团队的AlphaGo。因为我的研究方向是图像的有监督分类问题,故本文主要讲解生成对抗网络及其在分类问题方面的应用。
生成对抗网络框架
生成对抗网络(Generative adversarial networks,简称为GAN)是2014年由Ian J. Goodfellow首先提出来的一种学习框架,说起Ian J. Goodfellow本人,可能大家印象不深刻,但他的老师正是“深度学习三巨头”之一的Yoshua Bengio(另外两位分别是Hinton和LeCun),值得一提的是,Theano深度学习框架也是由他们团队开发的,开启了符号计算的先河。关于GAN在机器学习领域的地位,在这里引用一段Lecun的评价,
“There are many interesting recent development in deep learning…The most important one, in my opinion, is adversarial training (also called GAN for Generative Adversarial Networks). This, and the variations that are now being proposed is the most interesting idea in the last 10 years in ML, in my opinion.”
传统的生成模型都需要先定义一个概率分布的参数表达式,然后通过最大化似然函数来训练模型,比如深度玻尔兹曼机(RBM)。这些模型的梯度表达式展开式中通常含有期望项,导致很难得到准确解,一般需要近似,比如在RBM中,利用Markov chain 的收敛性,可以得到符合给定分布下的随机样本。为了克服求解准确性和计算复杂性的困难,J牛创造性的提出来了生成对抗网络。GAN模型不需要直接表示数据的似然函数,却可以生成与原始数据有相同分布的样本。
与常规的深度学习模型(比如cnn、dbn、rnn)不同,GAN模型采用了两个独立的神经网络,分别称为“generator”和“discriminator”,生成器用于根据输入噪声信号生成‘看上去和真实样本差不多’的高维样本,判别器用于区分生成器产生的样本和真实的训练样本(属于一个二分类问题)。其模型结构框架如下,
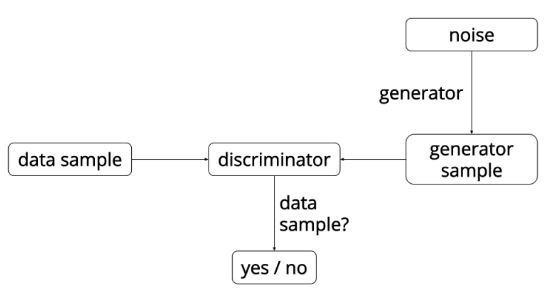 GANs是基于一个minimax机制而不是通常的优化问题,它所定义的损失函数是关于判别器的最大化和生成器的最小化,作者也证明了GAN模型最终能够收敛,此时判别器模型和生成器模型分别取得最优解。记$x$表示样本数据,$p(z)$表示生成器的输入噪声分布,$G(z; \theta_{g})$表示噪声到样本空间的映射,$D(x)$表示$x$属于真实样本而不是生成样本的概率,那么GAN模型可以定义为如下的优化问题, $$\min_{G}\max_{D}V(D, G)=E_{x~p_{data}(x)}[log D(x)]+E_{z~p_{z}(z)}[log(1-D(G(z)))] $$从以上公式可以看出,在模型的训练过程中,一方面需要修正判别器D,使值函数V最大化,也即使得$D(x)$最大化和$D(G(z))$最小化,其数学意义即最大化判别器分类训练样本和生成样本的正确率,另一方面需要修正生成器G,使值函数V最小化,也即使得$D(G(z))$最大化,其数学意义即生成器要尽量生成和训练样本非常相似的样本,这也正是GAN名字中Adversarial的由来。J牛提出了交替优化D和G(对D进行k步优化,对G进行1步优化),具体的训练过程如下,
GANs是基于一个minimax机制而不是通常的优化问题,它所定义的损失函数是关于判别器的最大化和生成器的最小化,作者也证明了GAN模型最终能够收敛,此时判别器模型和生成器模型分别取得最优解。记$x$表示样本数据,$p(z)$表示生成器的输入噪声分布,$G(z; \theta_{g})$表示噪声到样本空间的映射,$D(x)$表示$x$属于真实样本而不是生成样本的概率,那么GAN模型可以定义为如下的优化问题, $$\min_{G}\max_{D}V(D, G)=E_{x~p_{data}(x)}[log D(x)]+E_{z~p_{z}(z)}[log(1-D(G(z)))] $$从以上公式可以看出,在模型的训练过程中,一方面需要修正判别器D,使值函数V最大化,也即使得$D(x)$最大化和$D(G(z))$最小化,其数学意义即最大化判别器分类训练样本和生成样本的正确率,另一方面需要修正生成器G,使值函数V最小化,也即使得$D(G(z))$最大化,其数学意义即生成器要尽量生成和训练样本非常相似的样本,这也正是GAN名字中Adversarial的由来。J牛提出了交替优化D和G(对D进行k步优化,对G进行1步优化),具体的训练过程如下,

GAN在分类问题方面的应用
早期的GAN模型主要应用于无监督学习任务,即生成和训练样本有相同分布的数据,可以为1维信号或者二维图像。将GAN应用于分类问题时,需要对网络做改动,这里简单讲解一下已有的两篇文章中提出的方案,“Improved Techniques for Training GANs”和“Semantic Segmentation using Adversarial Networks”,前者可以归类于半监督分类算法,而后者则属于有监督分类算法。
半监督分类方法
将GAN应用于半监督分类任务时,只需要对最初的GAN的结构做稍微改动,即把discriminator模型的输出层替换成softmax分类器。假设训练数据有c类,那么在训练GAN模型的时候,可以把generator模拟出来的样本归为第c+1类,而softmax分类器也增加一个输出神经元,用于表示discriminator模型的输入为“假数据”的概率,这里的“假数据”具体指generator生成的样本。因为该模型可以利用有标签的训练样本,也可以从无标签的生成数据中学习,所以称之为“半监督”分类。定义损失函数如下,其中 L u n s u p e r v i s e d L_{unsupervised} Lunsupervised是一个标准的GAN优化问题,关于该模型的具体训练方法可以参见原文。
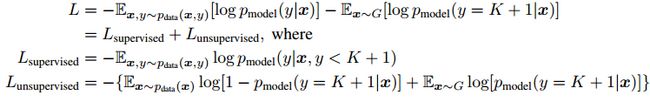
有监督分类方法
可想而知,在应用于基于像素的有监督分类问题时(文章中的训练数据集类似于人脸识别数据集,区别在于单幅图像的标签y和输入人脸图像大小相同),GAN中的生成器模型是没有什么作用的。原作者所提出的网络框架包含了两个分类器模型,其中一个用于对单幅图像进行基于像素的分类,另外一个分类器也称作对抗网络,用于区分标签图和预测出来的概率图,引入对抗网络的目的是使得得到的概率预测图更符合真实的标签图,具体的网络结构如下,
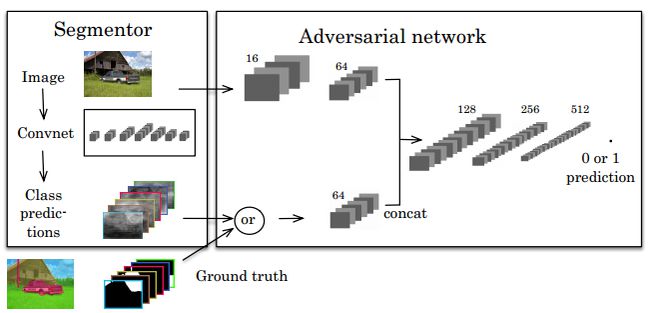 记训练图像为$\{x_{n}, y_{n}, n=1,...,N\}$,$s_{x}$表示预测出来的概率图,$a(x, y)$表示对抗网络预测y是x的真实标签图的概率,$\theta_{s}, \theta_{a}$分别表示segmentation模型和adversarial模型的参数,那么损失函数可以定义如下,$$L(\theta_{s}, \theta_{a})=\sum_{n=1}^{N}L_{mce}(s(x_{n}), y_{n})-\lambda[L_{bce}(a(x_{n}, y_{n}), 1)+L_{bce}(a(x_{n}, s(x_{n})), 0)]$$ 其中,$L_{mce}(y_1, y)$表示预测的概率图$y_1$和真实标签图y之间的multi-class cross entropy损失,而$L_{bce}(z1, z)=-[zln z1+(1-z)ln(1-z1)]$,即表示binary cross entropy 损失。与GAN的训练方法类似,这里的模型训练也是通过迭代训练adversarial模型和segmentation模型来完成的。在训练adversarial模型时,等价于优化如下表达式,其物理意义是使得adversarial模型对概率图和真实标签图的区分能力更强。 $$\sum_{n=1}^{N}L_{bce}(a(x_{n}, y_{n}), 1)+L_{bce}(a(x_{n}, s(x_{n})), 0)$$ 在训练segmentation模型时,等价于优化如下表达式,其物理意义是使得生成的概率图不仅和对应标签图相似,而且adversarial模型很难区分的开。 $$\sum_{n=1}^{N}L_{mce}(s(x_{n}), y_{n})-\lambda L_{bce}(a(x_{n}, s(x_{n})), 0)$$
记训练图像为$\{x_{n}, y_{n}, n=1,...,N\}$,$s_{x}$表示预测出来的概率图,$a(x, y)$表示对抗网络预测y是x的真实标签图的概率,$\theta_{s}, \theta_{a}$分别表示segmentation模型和adversarial模型的参数,那么损失函数可以定义如下,$$L(\theta_{s}, \theta_{a})=\sum_{n=1}^{N}L_{mce}(s(x_{n}), y_{n})-\lambda[L_{bce}(a(x_{n}, y_{n}), 1)+L_{bce}(a(x_{n}, s(x_{n})), 0)]$$ 其中,$L_{mce}(y_1, y)$表示预测的概率图$y_1$和真实标签图y之间的multi-class cross entropy损失,而$L_{bce}(z1, z)=-[zln z1+(1-z)ln(1-z1)]$,即表示binary cross entropy 损失。与GAN的训练方法类似,这里的模型训练也是通过迭代训练adversarial模型和segmentation模型来完成的。在训练adversarial模型时,等价于优化如下表达式,其物理意义是使得adversarial模型对概率图和真实标签图的区分能力更强。 $$\sum_{n=1}^{N}L_{bce}(a(x_{n}, y_{n}), 1)+L_{bce}(a(x_{n}, s(x_{n})), 0)$$ 在训练segmentation模型时,等价于优化如下表达式,其物理意义是使得生成的概率图不仅和对应标签图相似,而且adversarial模型很难区分的开。 $$\sum_{n=1}^{N}L_{mce}(s(x_{n}), y_{n})-\lambda L_{bce}(a(x_{n}, s(x_{n})), 0)$$
参考资料:Generative Adversarial Nets, Ian J. Goodfellow.
Improved Techniques for Training GANs. Tim Salimans, Ian Goodfellow.
Semantic Segmentation using Adversarial Networks. Pauline Luc.