第3章 基于PSO的已知静态路径规划方法

水面无人艇局部危险避障算法研究

Local Risk Obstacle Avoidance Algorithm of USV

博主 的硕士毕业论文

第3章 基于PSO的已知静态路径规划方法

　　水面无人艇在真实海域沿全局规划路径前进期间，由硬件（如AIS、航海雷达等）可探测到在电子海图上没有标示的障碍物信息。在无人艇行进的途中，必须对这些在全局路径规划时没有考虑到的障碍物进行规避，使其能够快速、安全的到达终点或子目标点。本章将针对障碍信息已知的静态障碍物路径规划问题展开研究，首先确定适应度函数和PSO中相关参数的取值，提出建立极坐标下的环境模型；运用启发式知识进行PSO初始化，并加入路径平滑优化处理方法，从而有效的提高了PSO的求解效率。最后通过仿真实验验证了本章提出算法的路径规划效果。

3.1 粒子群优化算法概述

3.1.1 粒子群优化算法的由来

　　粒子群优化算法（PSO, Particle Swarm Optimization），属于进化计算技术（evolutionary computation）领域，是一种集群优化算法，在1995年由Eberhart博士和Kennedy博士发明 [50] 。
　　PSO算法起源于对飞行鸟群觅食行为的研究。在鸟群捕食的时候，当有一只鸟发现不远处的食物后，它将飞向食物地点，这将导致它周围的其它鸟也沿着这个方向寻找食物地点，直到整个鸟群全部降落在此，找到食物。这是一种自然状态下的信息共享机制，在认知和搜寻过程中，个体会记住自身的飞行经验；同时，也向其它优秀个体学习，当它发现其它的某个个体飞行更好的时候，就会向它学习并对自身做出适当的调整，使得自己能朝着更好的方向飞行 [51] 。通过对这种自然现象的研究，可以知道，复杂的全局行为是通过简单规则的相互作用引发的；全局最优解是局部最优通过某种搜索规则，由种群中个体之间的相互协作而得到。同样作为基于群体迭代的一种进化计算技术，与遗传算法的不同之处是，PSO没有交叉、变异和复制等操作算子；而是粒子在空间内追随最优的粒子进行搜索 [35] 。

3.1.2 粒子群优化算法的基本原理

　　在粒子群算法中，把每一个问题所有可能的解都比喻成搜索空间内的一只鸟，然后抽象为没有体积和质量的粒子，并延伸至N维空间，而鸟群则简化为整个粒子群。鸟类彼此之间传递的有用消息相当于进化中的局部最优解，鸟群最终飞往的目的地相当于全局最优解，而鸟群行进的过程则相当于算法中的进化。粒子i在N维空间内的位置和速度分别用矢量来进行表示。
　　在PSO算法中，所有粒子都有一个已经确定的优化函数决定的适应值（Fitness Value），以及一个决定它们飞翔的方向和速度，然后所有的粒子按照自己的飞行经验追随自己发现的最优的粒子在搜索空间内搜索。PSO算法首先是初始化一群随机粒子，即随机解，然后通过迭代、进化找到最优解。在进化过程中，粒子通过两个极值更新自己，第一个是粒子在搜索过程中自己发现的最好位置（pbest），即局部最优值，第二个是粒子群中所有粒子发现的最佳位置（gbest），即全局最优值。每个粒子在不断改变自己的在搜索空间里的速度，来使自己尽量朝着pbest和gbest前进。
　　假设在n维搜索空间内，第i个粒子的位置和速度分别是 Xi=(xi,1xi,2……xi,N) 和 Vi=(vi,1vi,2……vi,N) ，每个粒子当前代数下自己找到的最优解为 Pi,d ，全局最优解为 Pg,d 。当找到这两个最优值时，按照以下公式得到迭代后各自新的位置和速度 [50] ：
　　 vi,d(t+1)=ωvi,d(t)+c1r1(pi,d−xi,d(t))+c2r2(pg,d−xi,d(t)) 　　(3-1)
　　 xi,d(t+1)=xi,d(t)+vi,d(t+1) 其中d=1,2,……,N　　(3-2)
　　其中： ω 为惯性权重；
　　　　　 r1 和 r2 是0-1之间均匀分布的随机数，用来增加种群多样性；
　　　　　 c1 和 c2 是学习因子，用来调控算法的局部收敛性。
　　PSO算法的性能很大程度上取决于粒子数、学习因子、惯性权重等参数的选取和控制，其中，部分参数的选取原则如下：
　　粒子数：粒子数的多少取决于实际问题的复杂程度；
　　粒子维度：由问题解的维度决定；
　　学习因子：该参数是粒子具备自我经验总结和学习能力的体现，通常取 c1 等于 c2 ，且在0-4之间；
　　惯性权重：该参数体现了粒子的继承性能，适当的选取可以保证粒子均衡的发展和具有探索能力。
　　作为一种优化搜索算法，PSO算法操作流程简单，参数简洁，收敛效果较好。从被提出到现在的近20年里，研究者们对算法的结构和性能作出了很多的改善。目前，尽管PSO有很多种变形和改进，但算法的核心依然是基于迭代的进化计算。基本的PSO算法的主要流程可参考图3-1：
　　由图可见，PSO算法步骤非常简单，没有复制、交叉、变异之类的操作算子，其核心就是按照式（1）更新其位置和速度信息，然后由两个“最优值”引导，完成搜索空间内的寻优。这也体现了PSO算法的简洁、容易的特性。

图3-1 基本PSO算法的主要流程图

3.1.3 粒子群算法在路径规划中的应用

　　PSO算法的提出，为很多复杂度较高的问题提供了一个新的思路和方法。近年来，其发展尤为迅速，在许多的领域内，都得到了广泛的应用，也取得了不错的效果。而PSO算法在路径规划中的应用可以说是异军突起，解决了很多复杂的全局路径规划和局部路径规划问题。其中，国内的秦元庆等使用Dijkstra法求得最小路径，再由PSO算法优化调整路径中的节点位置 [52] ；孙波等人提出，路径初始点应在开始—终点连线的若干垂直线上随机生成，并通过PSO算法优化调整路径位置点，其结果也证明了PSO能快速准确求解 [53] 。同时，也有部分学者从改进算法本身的角度出发，或者引入和结合其他算法，来提高全局求解精度和减小只能得到局部最优的可能性，实践结果也表明了多种算法的有效融合能显著提高局部寻优能力。
　　目前，在已有的较为成熟的PSO路径规划算法中，以一个粒子代表一条路径，每一条可能路径由一串路径关键点组成，粒子各个维度的分量则对应着路径上关键点与开始—终点连线的距离，再由算法的优化功能来调整路径点的位置。

3.2 极坐标系下的粒子群路径规划方法

　　本章要解决的问题是：基于环境先验知识的已知局部危险避障（静态障碍物），即无人艇局部危险避障的第一层。
　　无人艇路径规划问题可以描述为：在工作空间中搜索出一条从起始点到终止点的一条最优航线，这条航线不仅要满足无人艇的安全性条件，即不能与障碍物相撞，同时也要满足航线的路程最短，转弯次数最少。可以说，无人艇的已知局部危险避障问题可以归结为在可行区域中的优化搜索问题。

3.2.1 极坐标系下的建模

　　对于水面无人艇来说，基于环境先验知识的已知局部危险避障是一种在线路径规划策略，不仅要求路径最优，最重要的还需要满足较少的规划时间，即保证路径规划的时效性。
　　然而对于真实环境下，障碍物的形状各种各样，通过雷达扫描出来的雷达图像或通过声呐、传感器得到的障碍物形状可能会很复杂，直接对这些未经处理的障碍物形状进行避障，其计算过程往往会代价高昂，导致计算时间增加。为了减少计算消耗，缩短计算时间，在进行路径规划之前，需要对障碍物进行包围体处理，使障碍物形状得到合理的简化。
　　本文对障碍物的包围体处理包括两种方式：对于长宽比较小的障碍物用圆形进行包围，而对于长宽比较大的障碍物用有向包围盒 [42,54] （OBB，即具有方向性的矩形）进行包围。下面分别就两种障碍物处理方式进行说明。

3.2.1.1 障碍物圆形包围体的建模

　　对长宽比较小的障碍物来说，采用圆形进行障碍包围，不会损失太多的可行路径；而且在进行极坐标系下的PSO路径规划时，圆形包围体仅作为粒子中的一维进行处理，极大的简化了计算量，可以有效的缩短计算时长。外包圆具体取值方法为：其直径取障碍物所有顶点连线的最大值，即 r=max{|PiPj|/2} ，其中（i , j∈N， i ≠ j），圆心即为最大连线的中点，如图3-2所示。
　　则障碍圆在极坐标系下形成的曲线表示为：
　　 ρ2−2ρρicos(θ−θi)+ρi2=ri2 　　　(3-3)

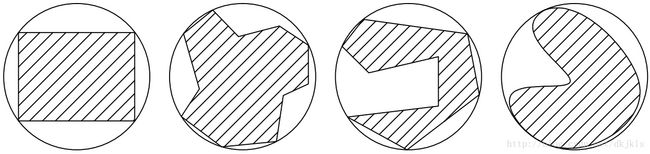
图3-2 障碍物圆形包围体建模示意图
　　其中 ρi 、 θi 、 ri 分别代表第i个障碍圆的极径、极角和直径， ρ 、 θ 则为第i个障碍圆上点的极径和极角。

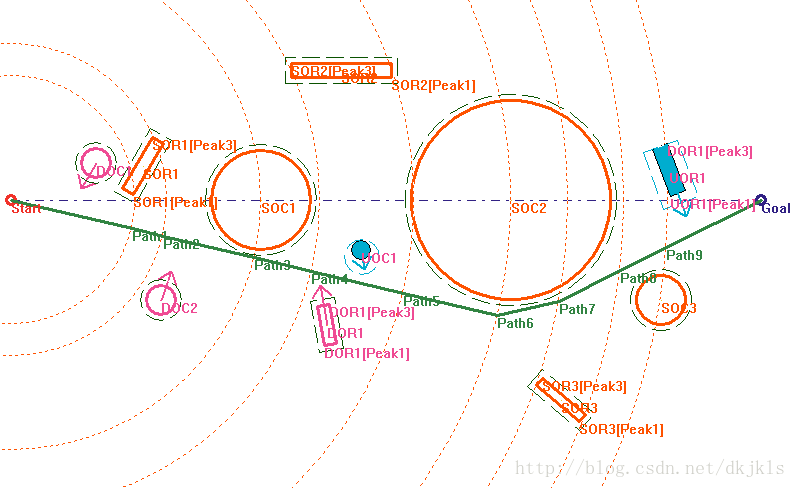
图3-3 极坐标系下环境模型的建立
　　无人艇在海面航行过程中，会存在许多不确定性因素，如障碍物运动的不确定性，无人艇本身运动的不确定性、执行机构运行时的不确定性、无人艇自身定位和对障碍物进行探测的系统也不可避免的存在误差等。由于存在诸多不确定性因素，且在本文的计算中，为了简化计算，将水面无人艇作为一个质心处理，所以需要对障碍物进行膨胀建模。对于障碍物的不确定性建模，本文将障碍物外包圆向外扩充一个安全阈值ε（本文取五倍船长）来进行膨胀处理，见图3-3中障碍圆（SOC1、SOC2、SOC3）各自外围的虚线所示。

3.2.1.2 障碍物有向包围盒的建模

　　在大部分无人艇避障研究中，对障碍物均采用圆形近似处理，且没有考虑到障碍物转向时的转向角度，丢失了大量的可行路径；甚至在多障碍物同时存在时，本可以横穿两障碍物中间区域的可行避障路径，却被判断为无效路径，从而导致无人艇需要花费更多的时间和能耗实现避障，最终导致无人艇宝贵的能源消耗快、续航力降低。如图3-4所示，在通过一处狭小水道时，若障碍物采用外包圆进行处理，则无人艇判断此种情况不可通过；然而，若采用有向包围盒进行障碍物处理，则无人艇可顺利通过此区域。
　　因为在海洋中无论是行驶中的船舶，还是海洋中的大型鱼类等，其长宽比均比较大，若仍采用外包圆进行处理，无疑会损失很多有效航行区域。所以针对长宽比较大的障碍物来说，将障碍物进行更贴合实际形状的模拟（即有向包围盒 [42,54] ，OBB）。虽然在进行极坐标系下的PSO路径规划时，一个有向包围盒作为粒子中的两维进行处理，增大了计算量，但采用此方法，可得到更多的有效路径区间，产生更优的避障路径，使得避障能耗更小、续航力更久。

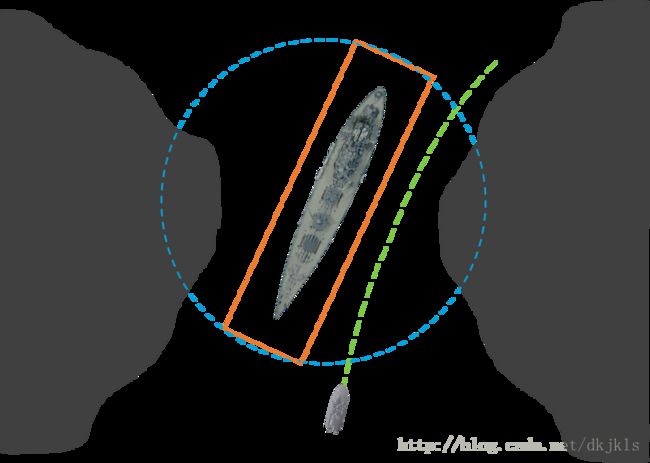
图3-4 障碍物外包圆和有向包围盒对比示意图
　　有向包围盒同样需要考虑诸多不确定性因素，矩形障碍物进行膨胀处理的方式同圆形障碍物，见图3-3中的SOR1、SOR2、SOR3。同时需要说明的是，为了便于计算，对于有向包围盒四个顶点的命名规则为：取极径最小的点为Peak0，剩下的三个点按逆时针进行命名。

3.2.1.3 极坐标系的建立

　　极坐标系的建立如图3-3所示。
　　其中“Start”代表起始点，“Goal”代表目标点。起始点和目标点的连线即为极坐标系的坐标轴，起始点Start为极点，逆时针方向为正。
　　对于基于PSO的已知静态路径规划中，需要确定记录路径节点信息的维度圆如图3-3中的橙色虚线。维度圆为以极点即起始点为圆心，每个障碍物的维度点的极径值为半径，得到的一组同心圆。外包圆的维度点为外包圆的圆心，有向包围盒的维度点有两点，分别为四个顶点中极径值位于中间的两点（有向包围盒维度点的选取详见3.2.3.2）。至此，就得到了一组同心圆，每一个同心圆都代表了粒子群中的一个维度，同心圆越多，环境越复杂。图3-3就是一个集已知、未知静动态障碍物并存的极坐标系下的环境建模图，其中包括3个已知静态圆形障碍物（SOC1，SOC2，SOC3），3个已知静态矩形障碍物（SOR1，SOR2，SOR3），2个已知动态圆形障碍物（DOC1，DOC2），1个已知动态矩形障碍物（DOR1），1个未知动态圆形障碍物（UOC1），1个未知动态矩形障碍物（UOR1）。

3.2.1.4 极坐标系中路径节点的存储方式

　　经过本文所提出的三层避障算法的解算得出的优化路径，是以路径关键点进行表示的，而在极坐标系下，关键点又是以该点的极径和极角表示的。
　　本文中节点的定义包括极径pm、极角pa、以该点为起点路径段的速度v，节点的结构体定义如下：
　　typedef struct { float pm;//极径
　　　　 　　　　　　float pa;//极角
　　　　 　　　　　　float v;//速度
　　　　 　　　　　}PolarCoordinate;
　　本文中路径关键点序列定义为一个路径节点类，该类的定义（只列出类中定义的数据）如下所示：
　　class Pathpoint { ·······························
　　　　 　　　　　　PolarCoordinate GeneralP;
　　　　 　　　　　　PolarCoordinate AdditionP;
　　　　 　　　　　　PolarCoordinate AdditionS;
　　　　 　　　　　　PolarCoordinate AdditionPU[NUM];
　　　　 　　　　　　PolarCoordinate AdditionSU[NUM];
　　　　 　　　　　　PolarCoordinate AdditionPUa[NUM];
　　　　 　　　　　　PolarCoordinate AdditionSUa[NUM];
　　　　 　　　　　};
　　类中的GeneralP为第一层基于PSO的已知静态路径规划所产生的路径常规点。
　　类中的AdditionS，AdditionP为第二层基于PSO并融合海事规则的已知动态路径规划所产生的附加点，其中AdditionS为起始点到一维路径节点之间的附加点，AdditionP为相应路径节点后的附加点。
　　类中的数组AdditionPU[NUM]，AdditionSU[NUM]，AdditionPUa[NUM]，AdditionSUa[NUM]为第三层基于滚动窗口的未知环境下的避障策略所产生的附加点，其中AdditionPU[NUM]为相应动态未知障碍物路径点（若该段无动态已知附加点，则仅有此值；若有动态已知附加点，则此值位于路径上半段），AdditionPUa[NUM]为相应动态未知障碍物路径点（表示此段有动态已知附加点，此值位于路径下半段），AdditionSU[NUM]为开始点到一维路径节点之间的动态未知障碍物路径点（若该段无动态已知附加点，则仅有此值；若有动态已知附加点，则此值位于路径上半段），AdditionSUa[NUM]为开始点到一维路径节点之间的动态未知障碍物路径点（表示此段有动态已知附加点，此值位于路径下半段）。

3.2.2 极坐标系下的PSO路径优化算法参数确定

　　经过大量实际应用验证表明，粒子群优化算法中的相关参数取值在各方面的应用中均起到了关键的作用，甚至直接影响到了算法的效率以及性能。
　　粒子群优化算法中涉及到的相关参数 [55] 有：惯性权值ω、学习因子c1和c2，和适应度函数。
　　（1） 惯性权值ω的取值
　　惯性权值ω作为粒子运动速度的系数，用来控制粒子飞行速度；同时也具有平衡算法全局搜索能力和局部搜索能力的作用。ω取值较小时，粒子速度的变化幅度较小，其局部搜寻能力较强，全局搜寻能力较弱；反之，ω取值较大时，粒子速度的变化幅度较大，其局部搜寻能力较弱，全局搜寻能力较强。所以说一个合适的ω取值可以很好的平衡全局搜索和局部搜索能力，最终可以以较少的迭代次数得到较优的解。
　　较为典型的ω取值方法有：
　　① 随机惯性权值(Random Inertia Weight,RIW)，即ω值在[0,1]取随机值。
　　② 模糊惯性权值(Fuzzy Inertia Weight,FIW)，该方法需要建立专家知识模糊规则，具有较大的实现难度，且对于路径规划问题不适用。
　　③ 线型递减惯性权重(Linearly Decreasing Weight, LDW),目前广泛采用的方法为线型递减权值，即：
　　 ω=ωmax−(ωmax−ωmin)∙runrunmax 　　　(3-4)
　　其中 ωmax 为最大惯性权重， ωmin 为最小惯性权重，run是当前迭代次数， runmax 为算法迭代的总次数。这种迭代方法在初期时全局搜索能力较强，后期局部搜索能力较强。
　　本文的惯性权值ω采取第三种方法，即线型递减惯性权重。
　　（2） 学习因子c1和c2的取值
　　适当的学习因子参数c1和c2可以有效的减少PSO在迭代过程中陷入局部最优解，加快粒子群收敛。较大的c1和c2会使粒子突然飞过目标区域；较小的c1和c2会使得种群在目标区域不断徘徊。而c1和c2通常为相等的常数，取值在0~4之间时，可搜索到较优的解。经过多次试验，本文c1和c2值均取为2.0。
　　（3） 适应度函数的确定
　　粒子群优化算法是通过适应度函数值来确定粒子的好坏的，是引导PSO向最优解逼近的决定性因素。可以说适应度函数选择的好坏，将直接影响算法的性能。
　　本文要求的性能指标，为一条长度最短的可行路径，且不能与障碍物相交。所以本文以路径长度值作为适应度函数值，式（3-5）表示路径长度值，其中 LPiPi+1 表示点i与点i+1之间的距离；适应度评价函数则为式（3-6）所示。
　　
　　 P=LSPi+∑n−1i=1LiLi+1+LPnG=∑ni=0LPiPi+1 　　　(3-5)
　　
　　 Fit(i)={LSG=∑ni=0LPiPi+1　　LPiPi+1∩NFD=∅+∞　　　　　　　　　　LPiPi+1∩NFD≠∅ 　　　(3-6)
　　
　　对于上面所说的适应度函数而言，取值越小说明粒子越优秀。如式（3-6）所示，适应度函数分为两个部分：可行避障路径与不可行避障路径。可行路径的适应度函数值即为最优路径的长度，不可行路径的适应度函数值设为无穷大。

3.2.3 路径可行性的判断

　　本节将对无人艇探测到的已知静态障碍物建立避障模型，进行几何分析。采用PSO进行路径规划过程中，假设已经计算到了第i维的路径点，下一步需要计算第i+1维上的路径点；此时PSO路径优化算法需要判断在第i+1维上有哪些圆弧段，是由于该维之前的障碍物阻碍导致不能进入的，而这些不能进入的圆弧段称之为该维的禁入域。
　　如图3-5所示，该状态为路径优化算法已经计算到了Path3这一点，下一步需要计算Dim4上的路径节点，图中共有F1、F2、F3三段禁入域，其中F1、F2分别为SOC2和SOC1产生的禁入域，F3为SOR1产生的禁入域。为了使计算更加快捷，本文采用动态计算禁入域，即计算到某一维的路径点时，只需计算该维之前障碍物所产生的禁入域，而该维后面的障碍物在本维中无需计算，从而节省了大量的计算量，缩短了计算时间。

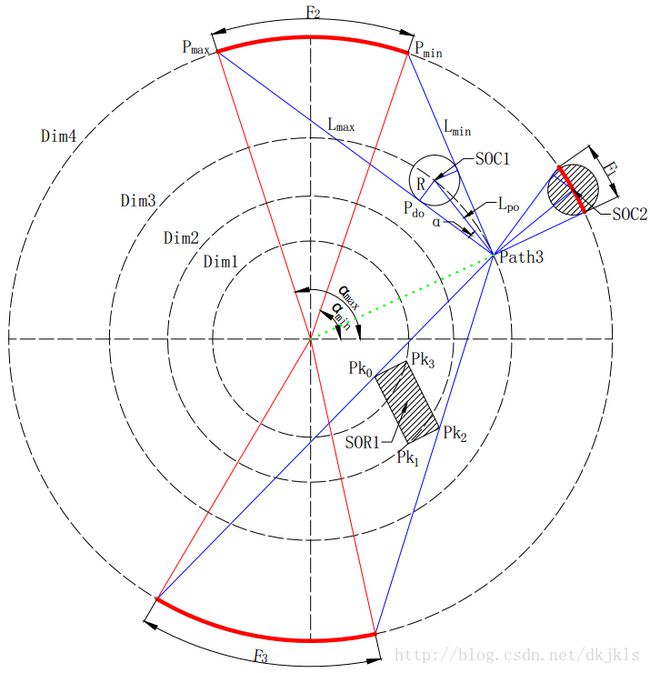
图3-5 障碍物禁入角求解示意图
　　同时为了方便计算路径点的极角，需要将这些禁入域转化为极坐标系下的对应禁入角。下面将就禁入角的求解，分为已知静态圆形障碍物和已知静态矩形障碍物进行说明。

3.2.3.1 已知静态圆形障碍物的禁入角求解

　　对于圆形障碍物禁入角，可分为三个部分进行处理：①本维度之前包括本维度上障碍物禁入角的求解；②若为最后一维，还需要计算最后一维与终止点之间的禁入角。
　　对于第二部分禁入角的求解，因为环境信息确定好之后，这部分的禁入角就已经确定了，而不会随着路径优化算法的进行而改变。所以，这部分禁入角的求解放在路径优化算法的循环之外进行，从而节省了（粒子数×迭代次数）次的计算量。
　　而第一部分禁入角的求解是随着路径优化算法的进行而改变的，所以需要在路径优化算法的循环之内进行。具体的求解方法如下：
　　如图3-5所示，以SOC1（已经过不确定性建模的膨胀处理）的禁入角求解为例进行说明。在路径点、障碍圆圆心、路径点与障碍圆外切切点组成的三角形中，路径点和障碍圆圆心的坐标值都为已知，通过这两点可求得两点之间线段的长度 Lpo ，以及该线段在极坐标系下的角度 θpo 。而两点连线和切线的交角α可通过式（3-7）求得。
　　 α=arcsinRLpo 　　　(3-7)
　　其中R为SOC1的半径加上安全阈值ε。
　　而切线段Lmin和Lmax的极角则可由θpo和α求得：
　　 {θLmin=θpo−αθLmax=θpo+α 　　　(3-8)
　　转换为笛卡尔坐标系下，继而可得到两条切线的斜率，加上线段上的路径点Path3，可得到切线的方程。在笛卡尔坐标系下求切线方程和Dim4圆方程，再通过切点 Pdo 的判断，便可得到禁入域的端点 Pmin 和 Pmax 的坐标值，从而可求得禁入角 αmin 和 αmax 。

3.2.3.2 已知静态矩形障碍物的禁入角求解

　　矩形障碍物也可分为两部分进行处理，处理方法同圆形障碍物禁入角。
　　同圆形障碍物求切线不同的是，矩形障碍物需要确认路径点属于矩形障碍物九个区域中哪个区域，有向包围盒区域划分编码见图3-6。而矩形障碍物禁入域的端点，也是由点处在矩形障碍物的位置决定的。如图3-5中的SOR1，点位于矩形的编码3中，则禁入域的两个端点分别为路径点与0点所确定的直线与本维圆的交点，和路径点与2点所确定的直线与本维圆的交点。具体求解方法详见圆形障碍物禁入域的求解。

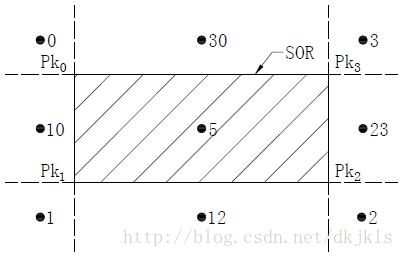
图3-6 有向包围盒区域划分编码示意图
　　对于矩形障碍物，还有一点需要说明的是其维度点的选取。
　　见图3-7所示，维度点的选取有（1）和（2）两种方式。对于（1）来说，虽然这种处理方式，使得Dim2上没有禁入角，减少了求解禁入角的计算量；但是会使得路径点可以取在维度圆上的任意一点，如图3-7（1）所示，从而导致在计算下一维路径点的时候，禁入域会很大，最终导致出现很不合理的路径。而维度点取为极径处于中间两点的方式，如图3-7（2），虽然增大了部分计算量，但会使得求得的最优路径更加合理。

图3-7 有向包围盒维度角选取示意图

3.2.3.3 其它的限制条件

图3-8 本维后面的障碍物覆盖本维维度圆情况示意图
　　（1）本文算法进行禁入域计算时，只计算了该维之前障碍物所产生的禁入域，还有一种情况需要进行考虑：后面的障碍物因过大或与上一维距离较近的情况下，覆盖了本维的维度圆，如图3-8中的SOC2覆盖了SOC1的维度圆，SOC4覆盖了SOC3的维度圆。对于这种情况需要确保路径点不能在障碍物扩展的圆或矩形中，所以在进行完禁入角的判断后，还需要对这种情况进行判断。
　　（2）无人艇最小回转直径的限制。
　　无人艇不能像陆上机器人那样可以快速的转向或改变速度，无人艇要改变其运动状态，需要一定的反应时间，并符合无人艇的最小回转直径的要求。所以对产生的路径节点，先根据无人艇当时运动的速度确定最小回转直径，再根据前后路径段的方向确定该节点最小回转圆形的圆心和回转圆弧段。并对回转圆弧段与障碍物进行相交运算，若与障碍物相交则判为不可行解。

3.2.4 引入启发式知识的初始化路径

　　启发式知识是指用与实际问题相关的知识和经验来指导问题的求解，可很好的提高算法的搜索能力，以及加快算法的收敛速度。
　　基本的粒子群优化算法是在工作区中随机的产生关键点，对于在极坐标系下则是随机的产生(-π~π]之间的角度值。然而对于本文所设立的极坐标系而言（极轴方向即为起点至目标点方向），预期的最优极角无疑应是在0°左右徘徊；若随机产生极角，会产生很多不必要的搜索操作，降低PSO的搜索效率。考虑到上述因素，本文在粒子初始化（即生成路径点极角）时，加入正态分布赋值函数，以期初始化产生相对极轴较小的偏转角度Δαi。本文所设置的正态分布初始化赋值符合正态分布N(0，(π/2) 2 )，并通过函数设置，只产生(-π~π]之间的角度值，Δα i 赋值分布图如图3-9所示。

图3-9 Δα i 初始化赋值分布图
　　加入正态分布初始化的粒子群路径规划算法，可使得初始化生成的路径上下颠簸幅度减少，同时可保证粒子群随机分布在较为合理的搜索空间中。

3.3 加入路径平滑优化处理的路径规划算法

3.3.1 引入启发式知识的基本粒子群优化算法的不足

　　对于本文采用PSO计算最优路径，若仅仅采用引入启发式知识的基本粒子群优化算法进行计算，会发现该方法在路径规划应用上的不足：
　　（1） 对于环境较为复杂的情况下，较多的障碍物会导致粒子群算法中的维数过大，从而会导致计算时间过长，并容易陷入局部最优的陷阱。
　　如图3-10中的情况所示，该环境下包括4个已知静态圆形障碍物和2个已知静态矩形障碍物，起始点和目标点之间的连线路径长度为4400m，每个粒子包括8个维度。设置粒子数为200，迭代次数为800，进行计算，图3-10中路径即为引入启发式知识的基本粒子群优化算法解算出的最优路径，图3-11为本次计算适应度值随迭代次数变化的情况。从图3-11可以看出算法在8代时就已得到了不是最优的收敛，并陷入了局部最优的状态，一直到第794代才得到了相对可行的路径，但确是消耗计算时间为代价的，进行本次计算的耗时为45.615s，显然是很不合理的一组解算。
　　（2） 引入启发式知识的基本粒子群优化算法在计算时，并未考虑过多的路径拐点对无人艇航行性能的要求。若将规划出来的路径直接作为航行路径，无疑会使无人艇在航行时经常改变航向，不仅做了很多没有必要的运动，而且会对无人艇的控制提出较高的机动性要求。
　　如图3-10中的情况所示，该环境为8个维度，在行进到每一个维度时都需要进行转向。

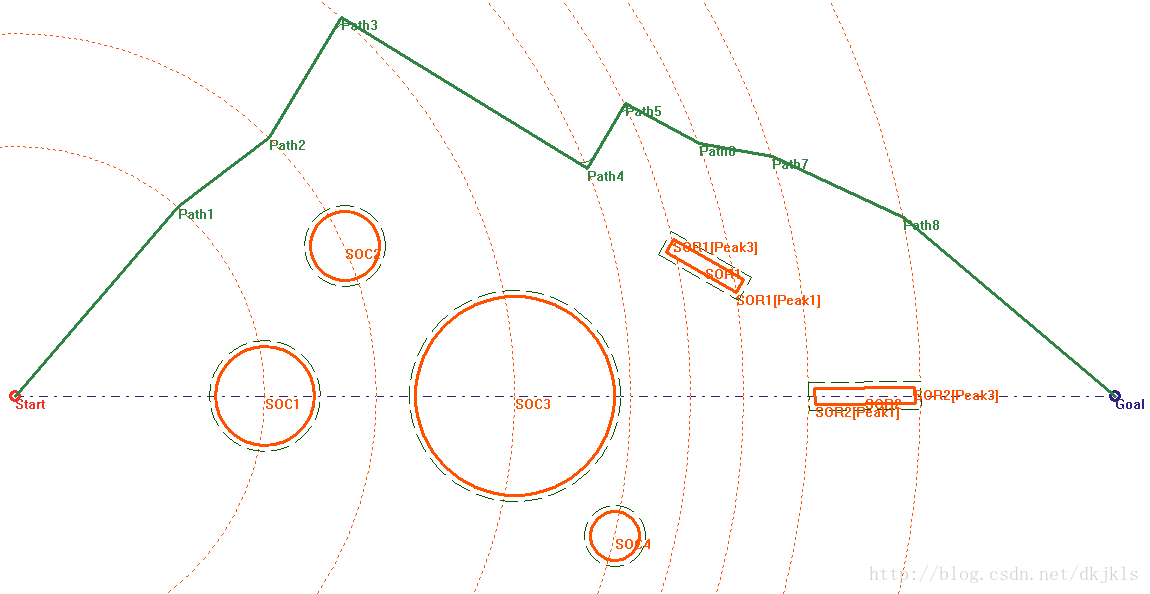
图3-10 引入启发式知识的基本粒子群优化算法解算最优路径示意图

图3-11 PSO适应度值随迭代次数变化情况

3.3.2 路径平滑优化处理方法

　　由于引入启发式知识的基本粒子群优化算法存在上述的不足，所以需要对该算法再引入路径平滑优化处理方法，使得算法得到最优解的耗时缩短、需转弯的次数最少。
　　本文采取的路径平滑优化处理方法为：
　　为了考虑全局最优性，从起始点开始与该点后面的路径点倒序相连，若该段连线不与障碍物相交，则选取这段连线为子路径段，并求出子路径段中间路径点的坐标值并赋予最优路径数组；直到求解到倒数第二个路径点为止。对于环境更为复杂的情况来说，进行一次路径平滑优化处理，还不足以得到最优的路径解，所以需要对优化后的路径多次进行优化，直到适应度函数值不再改变为止。
　　经过大量实验可以得出，采用加入路径平滑优化处理的PSO算法解算路径时，将PSO设置为粒子数100，迭代次数50，可以较好的平衡计算耗时和路径的最优解。
　　采用加入路径平滑优化处理的PSO算法对图3-10所示的情况再次进行计算，得到的最优路径如图3-12所示。该次计算所用耗时为1.576s，最优适应度函数值（即路径长度）为4492.992m；而所需转向的路径点为Path1、Path3、Path4这三处路径点，且从图上可以看出，每个转向点所需转向的角度都不大。

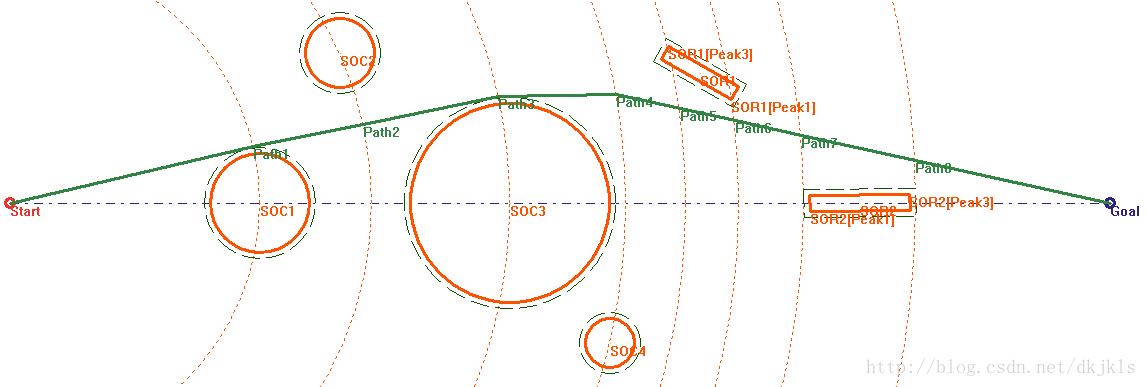
图3-12 采用加入路径平滑优化处理的PSO算法解算最优路径示意图
　　由此可以看出，对采用引入启发式知识的基本粒子群优化算法产生的路径的基础上，进行路径平滑优化处理，可以有效的缩短解算最优解的耗时，得到更优的路径解，减少无人艇航行时间，减少航行转向点数，减轻运动控制的负荷，对水面无人艇的安全高速航行有着重要的意义。

3.4 算法描述

　　结合本章对基于粒子群优化算法的已知静态路径规划方法，给出用于该算法的具体过程，其流程图见图3-13所示：

图3-13 基于PSO的已知静态路径规划方法流程图
　　需要说明的是，为达到降低解算时间，实时快速避障的目的，对粒子群优化算法中需要循环求解可行极角处，设定一个求解判断最大次数，若大于此值，就放弃此粒子在本代的解，以免陷入局部最优。在本算法中，需要设置求解最大次数的迭代处包括两个部分，下面分别来进行描述。
　　第一部分为“引入启发式知识的初始化种群”处，在该部分进行初始化时，需要设置每一维求解判断最大次数；若维数较大，在某一维处求解判断极角超过最大次数，此时需要退回上一维重新求解上一维的极角；同时需要设置进行此种回退方法的最大次数，超过最大次数则将该粒子作废。
　　第二部分为“是否处于可行域”处，该部分在更新粒子极角时，需要判断是否处在可行域，若不在可行域内，则继续求解。对此部分设置求解判断最大次数，若大于此值，就放弃此粒子在本代的解，该粒子的最佳适应度值设为之前代数所求解得到的最佳适应度值，以免陷入局部最优。

3.5 仿真实验结果及分析

　　本节将针对基于PSO的已知静态路径规划方法在Visual C++平台上进行仿真分析。分别对存在跨度较大的障碍物环境，和存在多个已知障碍物这两种环境下进行仿真实验。
　　在本节仿真实验中，均假定水面无人艇的全局最优路径为正东方，“Start”为起始点，“Goal”为终止点，起始点和目标点之间的连线路径长度为4400m，运行速度为40Kn；惯性权重ω采用线型递减策略，且ωmax=0.95，ωmin=0.2；c1=c2=2。

图3-14 基于PSO的已知静态路径规划方法情景一
　　情景一：如图3-14所示，该情景为存在跨度较大的障碍物SOC4，其中包括5个已知静态圆形障碍物和1个已知静态矩形障碍物（相关参数见表3-1和表3-2），每个粒子共七个维度。因环境中障碍物数目较少，设置粒子群迭代次数100，粒子数50；经过本文提出算法的解算，得到最优路径为4811.632m，计算耗时为1.170s，规划的路径节点见表3-3所列。可以得出采用本文提出的算法，计算耗时少，并能很好的穿行于障碍物中较为狭窄的可行通道，得到较为满意的优化路径。

表 3-1 情景一：已知静态矩形障碍物SOR参数

序号	中心点极径(m)	中心点极角(rad)	半长(m)	半宽(m)	方向角(°)
1	2973.214	6.094	200	32	30

表 3-2 情景一：已知静态圆形障碍物SOC参数

序号	极径(m)	极角(rad)	直径(m)
1	1000.00	0.000	400
2	1077.03	5.903	320
3	1969.77	5.865	800
4	2863.56	0.432	2800
5	3813.45	6.199	320

表 3-3 情景一：规划路径节点

路径点	极径(m)	极角(rad)
1	1000.000	5.535
2	1077.032	5.535
3	1969.772	6.171
4	2846.700	6.203
5	2863.564	6.204
6	3111.740	6.223
7	3813.448	6.261

图3-15 基于PSO的已知静态路径规划方法情景二

　　情景二：如图3-15所示，该情景为存在多个已知障碍物，其中包括9个已知静态圆形障碍物和3个已知静态矩形障碍物（相关参数见表3-4和表3-5），每个粒子共15个维度。因环境中障碍物数目较多，为了平衡计算耗时和最优路径之间的矛盾，设置粒子群迭代次数50，粒子数50；经过本文提出算法的解算，得到最优路径为4782.844m，计算耗时为2.449s，规划的路径节点见表3-6所列。可以得出采用本文提出的算法，计算耗时少，最优路径较为合理。

表 3-4 情景二：已知静态矩形障碍物SOR参数

序号	中心点极径(m)	中心点极角(rad)	半长(m)	半宽(m)	方向角(°)
1	517.362	5.969	280	40	90
2	3400.941	0.024	280	40	160
3	3972.908	0.081	280	40	160

表 3-5 情景二：已知静态圆形障碍物SOC参数

序号	极径(m)	极角(rad)	直径(m)
1	1000.000	0.000000	400.000
2	1413.648	5.845000
3	1708.800	0.359000	440.000
4	2000.000	0.000000	800.000
5	2443.932	5.915000	320.000
6	2630.588	6.131000	200.000
7	2891.088	0.252000	280.000
8	3038.156	6.125000	600.000
9	3492.848	0.231000	400.000

表 3-6 情景二：规划路径节点

路径点	极径	极角	路径点	极径	极角	路径点	极径	极角
1	574.344	0.533	6	2000.000	0.457	11	3145.708	0.139
2	631.252	0.533	7	2443.932	0.289	12	3492.848	0.090
3	1000.000	0.533	8	2630.588	0.240	13	3664.744	0.069
4	1413.648	0.533	9	2891.088	0.184	14	3727.792	0.062
5	1708.800	0.533	10	3038.156	0.157	15	4226.652	0.014

　　为了验证本章所设计的基于PSO的已知静态路径规划方法，设立了以上两种情况。仿真实验结果及分析表明，该算法具有较强的环境适应能力，计算速度快，收敛精度较高。
　　本章的研究为下一步处理动态已知、动态未知障碍物的实时在线规划奠定了坚实的基础。

博主 的硕士毕业论文

===========文档信息============
版权声明：非商用自由转载-保持署名-注明出处
署名(BY) ：dkjkls（dkj卡洛斯）
文章出处：http://my.csdn.net/dkjkls