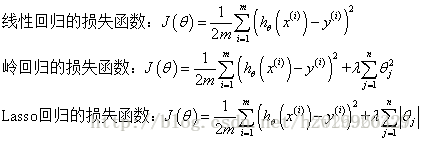机器学习实战第八章 - 预测数值型数据：回归

一，线性回归

1，线性回归的特点

线性回归

• 优点：结果易于理解，计算上不复杂
• 缺点：对非线性的数据拟合不好
• 适用数据类型：数值型和标称型数据

2，线性回归的要素

(1)线性回归模型：

h(xi)=xTi∗w

(2)目标函数：

J(w)=12m∑i=1m(yi−h(xi))

(3)最优化方法：梯度下降法或者正规方程法。

正规方程法：首先对 J(w) 求 w 的偏导，然后令各个偏导为0，，即可求得w。具体过程如下：
J(w) 的向量形式为 （Y−Xw)T(Y−Xw) ，对 w 求导，得到 XT(Y−Xw) ，令其为0，即可得到 w 的值为： w^=(XTX)−1XTy 。

3，Python代码实现(使用正规方程求解w)

from numpy import *
def loadDataSet(filename):
    dataMat = []
    yMat = []
    numFeat = len(open(filename).readline().split('\t'))-1
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        yMat.append(float(curLine[-1]))
    return dataMat,yMat
def standRegress(xArr,yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx)==0.0:
        print('The xTx is singular,cannot do inverse...')
        return
    xTy = xMat.T*yMat
    ws = xTx.I*xTy
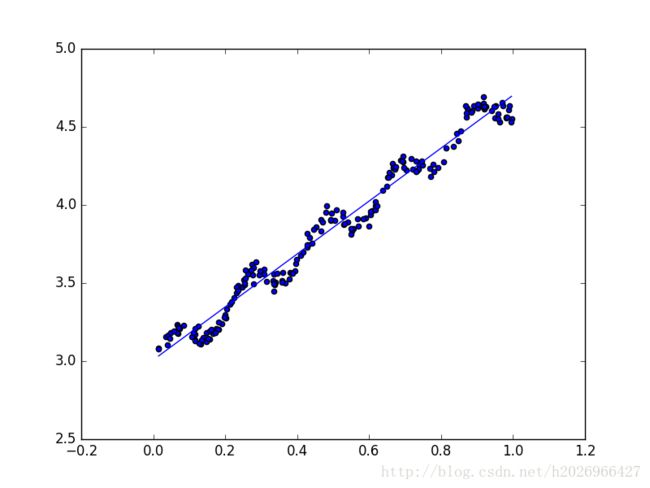
    return ws

图像如下：

并且预测值与真实值之间的相关系数很高，为0.997：

>>> corrcoef(yHat.T,yMat)
array([[ 1. , 0.99658327], [ 0.99658327, 1. ]])

二，局部加权线性回归

1，什么是局部加权线性回归

因为线性回归很可能出现欠拟合现象，因为它求的是具有最小均方误差的无偏估计。所以当模型欠拟合时，不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。

其中一个方法就是局部加权线性回归（Locally Weighted Linear Regression，LWLR）。
该算法中会给待预测点附近的每个点赋予一定的权重，然后再基于最小均方误差来求得：

w^=(XTWX)−1XTWy

其中 W 是一个对角矩阵，用来给每个数据点赋予权重。

该方法主要使用“核函数”来给附近的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下：

w(i,i)=exp(|xi−x|−2k2)

这样就可以构建一个只含对角元素的权重矩阵 W ，并且点 x 与 xi 越近， w(i,i) 就越大。

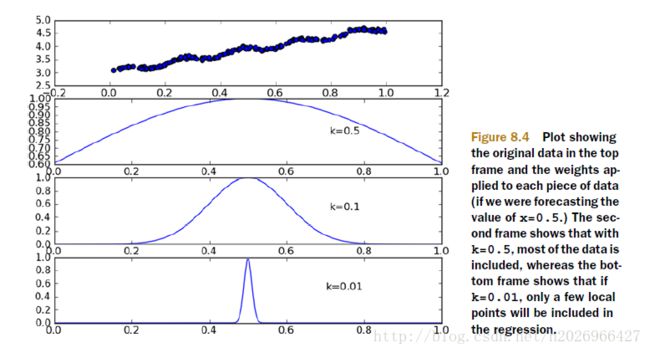
其中参数k决定了对待预测点附近的点赋予多大的权重。
如下图所示参数k与权重的关系：

2，Python代码实现

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye(m))
    for i in range(m):
        diffMat = testPoint - xMat[i,:]
        weights[i,i] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T*weights*xMat
    if linalg.det(xTx) == 0.0:
        print('xTx is singular,cannot do inverse.')
        return
    xTy = xMat.T*(weights*yMat)
    ws = xTx.I*xTy
    return testPoint*ws
def lwlrTest(testArr,xArr,yArr,k=1.0):
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
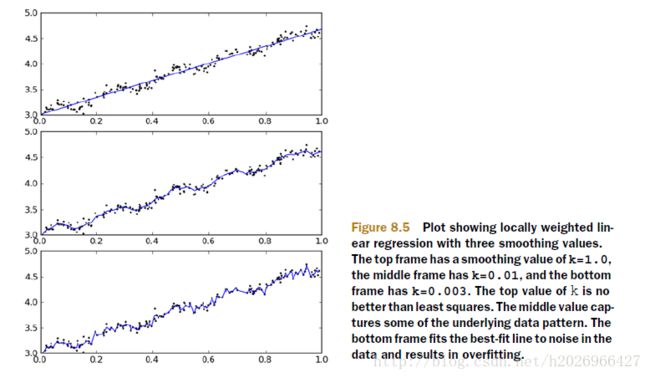
    return yHat

当参数k为0.003时，预测的回归函数如下：

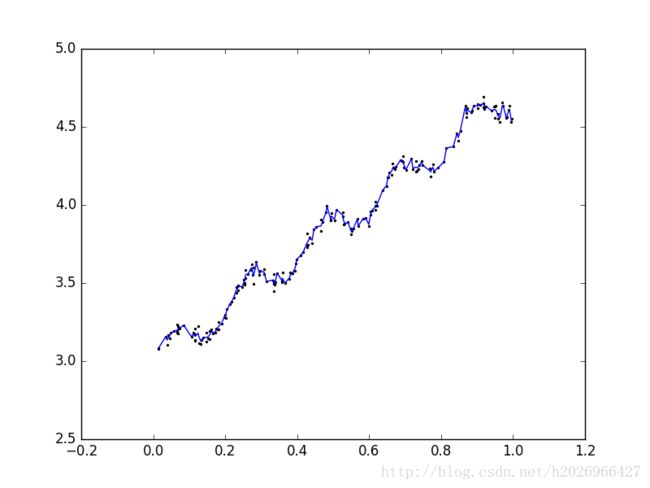
显然有些过拟合！

当设置不同k可得到不同的回归函数的图像如下：

可以看出

• k=1.0时，模型欠拟合
• k=0.003时，模型过拟合
• k=0.01时，模型较准确

3，局部加权线性回归的特点

局部加权线性回归的的主要问题在于它增加了计算量，因为它对每个点预测时都必须使用整个数据集，因为需要用整个数据集计算出数据集中每个点与特定待预测点的相似度（这里相似度用核函数来计算），用来当做每个点的权重。待预测点不同数据集中每个点的权重也不同！

三，缩减系数来理解数据

本质上是加入正则化项，因为正则化项的加入，所以会将一些不重要特征的系数缩减成较小的值或者直接缩减为0。还可以看做是对一个模型增加偏差的同时减小方差。

一般需要先对数据进行标准化处理。

主要方法包括：

• 岭回归（加入L2正则项）
• Lasso回归（加入L1正则项）
• 前向逐步回归

其中Lasso回归会倾向于将一些不重要的特征的回归系数置为0，所以它也可以作为一种特征选择的方法。