小朋友学十大排序算法（1）：冒泡排序

一、基本原理（由小到大）

将相邻两个数比较，将大的调到后头。如果有n个数，则要进行n-1趟比较。
在第1趟中要进行n-1次两两比较，在第j趟比较中要进行n-j次两两比较。

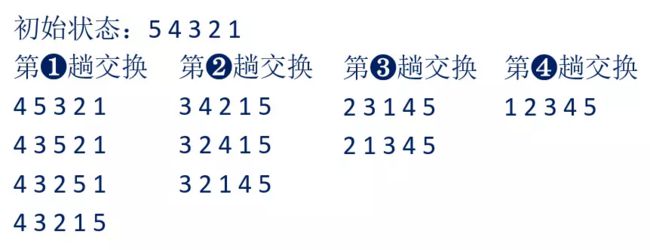
上图中有5个数，要进行5 - 1 = 4趟比较。
第1趟，要进行n - 1 = 4次两两比较；
第2趟，要进行5 - 2 = 3次两两比较；
第3趟，要进行5 - 3 = 2次两两比较；
第4趟，要进行5 - 4 = 1次两两比较。

二、代码实现

#include 

// 打印数组，方便观察结果
void print_array(int a[], int n)
{
	for(int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

// 冒泡排序算法
void bubble_sort(int a[], int n)
{
    // j表示第几轮比较
    for(int j = 0; j < n - 1; j++)
    {
        // i表示待比较的第几个元素
        for(int i = 0; i < n - 1 - j; i++)
        {
            if(a[i] > a[i+1])
            {
                a[i] ^= a[i+1];
                a[i+1] ^= a[i];
                a[i] ^= a[i+1];
            }
			
			// 打印每一轮比较，每次交换后的结果
			print_array(a, n);
        } 
		printf("********************\n");
    }
} 

int main ()
{
    int a[] = {5, 4, 3, 2, 1};
	int count = sizeof(a) / sizeof(int); // 求数组元素个数
    bubble_sort(a, count);
	
    return 0;
}

分析：
bubble_sort函数中，有两层循环。外层用j来自增，内层用i来自增。
外层的循环自增的慢，内层的循环自增的快。
内层的循环i要都自增完，外层的j才会自加1。

执行过程为：
j = 0, i = 0, if(a[0] > a[1])为真，a[0]与a[1]交换，数组变为{4,5,3,2,1}
j = 0, i = 1, if(a[1] > a[2])为真，a[1]与a[2]交换，数组变为{4,3,5,2,1}
j = 0, i = 2, if为真，a[2]与a[3]交换，数组变为{4, 3, 2, 5, 1}
j = 0, i = 3, if为真，a[3]与a[4]交换，数组变为{4, 3, 2, 1, 5}，
此时最大的5已经挪到最后的位置，接下来5就不用再处理。

j = 1, i = 0, if为真，a[0]与a[1]交换，数组变为{3, 4, 2, 1, 5}
j = 1, i = 1, if为真，a[1]与a[2]交换，数组变为{3, 2, 4, 1, 5}
j = 1, i = 2, if为真，a[2]与a[3]交换，数组变为{3, 2, 1, 4, 5}，
此时4已经挪到倒数第二个位置，接下来4和5就不用再处理。

j = 2, i = 0, if为真，a[0]与a[1]交换，数组变为{2, 3, 1, 4, 5}
j = 2, i = 1, if为真，a[1]与a[2]交换，数组变为{2, 1, 3, 4, 5}，
此时3已经挪到倒数第三个位置，接下来3、4和5就不用再处理。

j = 3, i = 0, if为真，a[0]与a[1]交换，数组变为{1, 2, 3, 4, 5}，
此时2已经挪到倒数第四个位置，接下来2、3、4和5就不用再处理。
剩余一个数1，也不用交换了。至此排序完毕。

输出结果：

4 5 3 2 1 
4 3 5 2 1 
4 3 2 5 1 
4 3 2 1 5 
********************
3 4 2 1 5 
3 2 4 1 5 
3 2 1 4 5 
********************
2 3 1 4 5 
2 1 3 4 5 
********************
1 2 3 4 5 
********************

三、时间复杂度

以{5，4，3，2，1}为例。
第1趟，要进行n - 1 = 4次两两比较；
第2趟，要进行5 - 2 = 3次两两比较；
第3趟，要进行5 - 3 = 2次两两比较；
第4趟，要进行5 - 4 = 1次两两比较。
总共比较了4 + 3 + 2 + 1 = 10次。
如果是n个数，比较的次数为(n - 1) + (n - 2) + … + 2 + 1 = n(n - 1) / 2次。所以时间复杂度是O(n2)。

四、稳定性

若排序的过程中，两个相同的数据，其先后顺序不会发生变化，则称这种排序方法是稳定的，否则就是不稳定的。
以对{5，2，2，1}进行冒泡排序为例。这个数列里有两个2，排序过程为：
5，2，2，1
2，5，2，1
2，2，5，1
2，2，1，5
2，2，1，5
2，1，2，5
1，2，2，5
从整个过程可以看出，两个2的相对一直都保持不变，所以，冒泡排序是稳定的排序算法。
后面的课程中，会接触到不稳定的排序算法。

少儿编程QQ群：581357582，少儿英语QQ群：952399366，微信：307591841