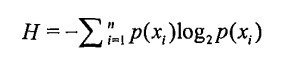机器学习实战_03-决策树

决策树
优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配问题。
适用数据类型：数值型和标称型。

使用：
决策树被经常用于专家系统中。

步骤：
我们需要学习如何从一堆原始数据中构造决策树。
首先我们讨论构造决策树的方法，以及如何编写构造树的python代码；
接着提出一些度量算法成功率的方法；
最后使用递归建立分类器，并且绘制决策树图。

原理：
得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。
第一次划分之后，数据将被向下传递到树分支的下一个节点，在这个节点 上，我们可以再次划分数据。
因此我们可以采用递归的原则处理数据集。
递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。
如果所有实例具有相同的分类，则得到一个叶子节点或者终止块。
任何到达叶子节点的数据必然属于叶子节点的分类

划分数据集的最大原则：
将无序的数据变得更加有序。我们可以使用多种方法划分数据集，但是每种方法都有各自的优缺点。组织杂乱无章数据的一种方法就是使用信息论度量信息， 信息论是量化处理信息的分支科学。我们可以在划分数据之前使用信息论量化度量信息的内容。
在划分数据集之前之后信息发生的变化称为信息增益， 知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

具体实现：
创建分支的伪代码函数createBranch()如下

检测数据集中的每个子项是否属于同一分类：
    If so return 类标签；
    else
        寻找划分数据集的最好特征
        划分数据集 
        创建分支节点
            for 每个划分的子集
                调用函数createBranch并增加返回结果到分支节点中
        return 分支节点

1. 计算香农熵，计算信息增益

计算公式：

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] +=1
        shannotEnt=0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannotEnt -=prob*log(prob,2)
    return shannotEnt

2.根据给定特征划分数据集

def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis]==value:
            reduceFeatVec = featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reduceFeatVec)
    return retDataSet

3.选择最好的数据集划分方式

def chooseBeatFeatureToSplite(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoFain = 0.0; bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoFain):
            bestInfoFain = infoGain
            bestFeature = i
    return bestFeature

辅助函数：
遍历完所有特征时返回出现次数最多的

def majorityCnt(classList):
    classCount ={}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]= 0
        classCount[vote] +=1
    sortedClassCount = sorted(classCount.iteritems(),key = operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

4. 递归构建决策树

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0])==1:
        return majorityCnt(classList)
    bestFeat = chooseBeatFeatureToSplite(dataSet)
    beatFeatureLabel = labels[bestFeat]
    myTree = {beatFeatureLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[beatFeatureLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

5. 自己构建数据集

def creatDataSet():
    dataSet = [[1,1,'yes'],[1,0,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
    labels = ['no surfacing','flippers']
    return dataSet,labels

使用案例：

myDat ,labels =creatDataSet() myTree = createTree(myDat ,labels)