聚类分析

  聚类常用于数据探索或挖掘前期，在没有做先验经验的背景下做的探索性分析，也适用于样本量较大情况下的数据预处理工作。例如针对企业整体的用户特征，在未得到相关只是或经验之前先根据数据本身特点进行用户分群，然后针对不同群体做进一步分析；例如对连续数据做离散化，便于后续做分类分析应用。

  常用的聚类算法分为基于划分，层次，密度，网格，统计学，模型等类型的算法，典型算法包括K均值（经典的聚类算法），DBSCAN，两步聚类，BIRCH，谱聚类等。

  聚类分析能解决的问题包括：数据集可以分位几类，每个类别有多少样本量，不同类别中各个变量的强弱关系如何，不同类别的典型特征是什么等；除了划分类别外，聚类还能用于基于类别划分的其他应用，例如图片压缩等。但是，聚类无法提供明确的行动指向，聚类结果更多是为后期挖掘和分析工作提供预处理和参考，无法回答“为什么”和“怎么办”的问题。

数据异常对聚类结果的影响

  K均值（K-Means）是聚类中最常用的方法之一，它基于点与点距离的相似度来计算最佳类别归属，但K均值在应用之前一定要注意两种数据异常：

1. 数据的异常值。数据中的异常值能明显改变不同点之间的距离相似度，并且这种影响是非常显著的。因此基于距离相似度的判别模式下，异常值的处理必不可少。
2. 数据的异常量纲。不同的维度和变量之间，如果存在数值规模或量纲的差异，那么在做距离之前需要先将变量归一化或标准化。例如跳出率的数值分布区间是[0,1],订单金额可能是[0,10 000 000],而订单数量则是[0,1000],如果没有归一化或标准化操作，那么相似度将主要受订单金额的影响。

超大数据量时应该放弃K均值算法

  K均值在算法稳定性，效率和准确率（相对于真实标签的判别）上表现非常好，并且在应对大量数据时依然如此。它的算法时间复杂度上界为O(nkt)，其中n是样本量，k是划分的聚类数，t是迭代次数。当聚类数和迭代次数不变时，K均值的算法消耗时间只跟样本量有关，因此会呈线性增长趋势。

应对高维数据的聚类

  在做高位数据聚类时，传统的在低维空间通用的聚类方法运用到高维度空间时，通常不能取得令人满意的聚类效果，这主要表现在聚类计算耗时太长，聚类结果相对于真实标签分类的准确性和稳定性都大大降低。问什么在高维空间下聚类会出现这种问题呢？

• 在面对高维数据时，基于距离的相似度计算效率极低；
• 高维空间的大量属性特征使得在所有维上存在簇的可能性非常低；
• 由于稀疏性及近邻特性，基于距离的相似度几乎为0，导致高维的空间中很难存在数据簇。

在应对高维数据的聚类主要有2种方法：降维，子空间聚类。

• 降维是应对高维数据的有效办法，通过特征选择法或维度转化法将高维空间降低或映射到低维空间，直接解决了高维问题。
• 子空间聚类算法是在高维数据空间中对传统聚类算法的一种扩展，其思路是选取与给定簇密切相关的维，然后在对应的子空间进行聚类。比如谱聚类就是一种子空间聚类方法。由于选择相关维的方法以及评估子空间的方法需要自定义，因此这种方法对操作者的要求较高。

如何选择聚类分析算法

聚类算法有几十种之多，聚类算法的选择，主要参考以下因素：

• 如果数据集是高维度的，那么选择谱聚类，它是子空间划分的一种。
• 如果数据量为中小规模，例如在100W条以内，那么K均值将是比较好的选择；如果数据量超过100W条，那么可以考虑使用Mini Batch KMeans。
• 如果数据集中有噪点（离群点），那么使用基于密度DBSCAN可以有效应对这个问题。
• 如果追求更高的分类准确度，那么选择谱聚类将比K均值准确度更好。

Python 聚类分析

import numpy as np 
import matplotlib.pyplot as plt


# 数据准备
raw_data = np.loadtxt('/Users/nxcjh/learn/python-yunying/python_book/chapter4/cluster.txt') # 导入数据文件
X = raw_data[:, :-1] # 分割要聚类的数据
y_true = raw_data[:, -1] 

print(X)

[[ 0.58057881  0.43199283]
 [ 1.70562094  1.16006288]
 [ 0.8016818  -0.51336891]
 ...
 [-0.75715533 -1.41926816]
 [-0.34736103 -0.84889633]
 [ 0.61103884 -0.46151157]]

训练聚类模型

训练聚类模型。先设置聚类数量为3，并建立聚类模型对象，然后通过fit方法训练模型，通过predict方法做聚类应用得到原始训练集的聚类标签集y_pre(也可以在应用fit方法后直接从聚类对象的labels_属性获得训练集的聚类标签)；从得到的聚类模型中，通过其cluster_centers_ 属性和inertia_属性得到各类别中心以及样本距离最近的聚类中心的总和。

from sklearn.cluster import KMeans # 导入Sklearn聚类模块

n_clusters = 3 # 设置聚类数量
model_kmeans = KMeans(n_clusters=n_clusters, random_state=0) # 建立聚类模型对象

知识点：将算法保存到硬盘

Python 内置标准库cPickle是实现这一过程的有效方法库。cPickle可以将任意一种类型的Python将对象进行序列化/持久化操作，算法模型对象也不例外。cPickle的主要应用方法是dump和load。

• dump: 将Python对象序列化保存到本地的文件
• load: 从本地文件读取Python对象并恢复实例对象

注意：在python3中使用pickle，python2中使用cPickle

import pickle
pickle.dump(model_kmeans, open("my_model_object.pkl","wb"))
model_kmeans2 = pickle.load(open("my_model_object.pkl","rb"))

model_kmeans2.fit(X) # 训练聚类模型
y_pre = model_kmeans2.predict(X) # 预测聚类模型
print(y_pre)

[1 1 2 0 2 0 1 1 0 0 0 1 2 1 2 1 0 2 2 2 2 2 1 2 1 0 0 1 1 0 0 2 2 2 0 0 2
 0 1 2 2 2 1 1 2 2 2 1 1 0 0 1 1 1 0 2 0 2 1 0 1 0 1 1 0 2 2 2 1 1 1 0 1 1
 0 1 1 2 1 1 1 0 2 1 2 0 0 1 0 1 2 0 0 1 1 1 2 0 0 1 2 1 1 0 2 1 0 2 1 1 2
 1 2 1 2 2 0 0 1 1 2 2 1 1 0 1 1 1 2 1 1 0 2 2 1 2 0 1 2 1 0 2 2 1 2 2 2 1
 2 1 1 0 1 1 0 0 2 1 1 1 1 1 2 2 1 1 0 0 1 0 2 2 1 2 0 1 0 1 1 1 0 0 0 2 0
 1 0 0 2 0 1 2 0 1 0 0 0 1 2 0 2 1 2 0 2 1 1 2 1 1 1 1 1 1 2 2 0 2 0 1 0 1
 1 1 2 2 2 0 1 2 0 0 2 2 1 0 2 2 1 1 2 2 1 2 2 0 2 2 2 1 0 1 2 2 2 1 2 0 0
 1 2 2 2 0 1 2 2 2 2 2 0 0 1 0 0 1 1 0 0 1 2 0 2 0 1 2 2 0 0 1 1 0 1 2 2 0
 0 2 1 1 0 1 1 1 2 1 2 1 2 0 2 0 1 0 1 0 0 1 2 0 2 2 1 0 0 0 2 0 1 0 1 0 1
 2 1 2 2 0 0 1 0 1 2 2 1 2 0 2 2 1 1 1 1 2 2 2 2 2 2 1 2 1 0 2 2 0 1 2 0 2
 1 2 2 1 2 2 2 2 2 2 0 2 0 0 2 0 1 2 2 2 0 2 0 0 1 2 1 0 0 1 2 0 2 1 1 0 1
 0 0 0 0 0 2 1 2 0 1 1 0 2 2 2 1 2 1 2 2 0 2 2 2 0 1 0 1 1 1 0 0 1 0 0 2 0
 1 0 1 1 1 2 0 2 2 2 0 1 0 1 1 1 1 1 1 0 1 2 1 1 1 2 2 2 2 2 2 0 0 2 0 0 1
 0 1 2 1 0 0 0 2 1 2 1 2 2 0 0 0 0 1 1 1 0 2 0 0 1 0 2 0 2 0 1 1 2 1 1 2 0
 1 0 1 0 0 0 0 0 2 2 0 1 2 0 0 1 1 1 0 1 2 2 0 1 2 1 2 2 2 1 2 0 1 1 1 2 0
 0 1 1 0 2 0 2 2 2 1 0 2 0 0 0 1 0 1 1 0 2 2 0 1 1 1 2 2 1 2 1 2 1 0 0 2 0
 2 2 0 0 1 0 1 2 2 1 0 1 2 2 1 0 0 0 1 1 1 0 2 2 0 2 2 2 0 1 2 2 2 0 2 1 1
 0 0 0 0 0 0 1 2 1 1 1 2 2 2 1 0 1 2 2 1 0 2 1 2 2 0 1 0 1 0 0 2 1 2 0 0 1
 0 2 0 2 1 0 2 1 1 1 0 0 1 2 2 1 2 2 0 0 1 1 0 2 0 1 1 2 0 2 1 0 0 2 2 1 1
 1 0 0 2 1 0 1 2 0 0 2 0 2 0 1 2 1 0 0 1 1 2 1 1 1 0 0 1 2 2 0 0 2 0 2 0 1
 1 0 0 0 1 0 0 0 1 0 1 2 2 0 0 2 2 1 0 0 0 2 1 0 1 0 1 2 2 0 0 1 2 2 1 0 2
 2 1 0 2 1 2 2 1 2 1 2 2 0 0 0 0 2 2 1 1 2 1 1 1 0 1 0 2 1 0 2 1 2 1 2 0 2
 0 1 0 1 1 1 0 2 2 0 0 1 0 0 0 0 0 0 0 2 0 2 0 2 2 0 1 0 2 1 2 1 2 1 2 0 2
 1 2 1 2 2 2 0 2 0 0 0 0 2 0 0 1 1 0 0 2 1 1 0 2 0 1 2 0 2 2 1 1 1 1 0 2 1
 1 0 0 1 0 2 2 1 2 1 0 2 0 1 1 2 0 1 2 0 1 0 1 1 1 1 0 1 2 0 1 0 2 0 0 0 0
 0 1 1 2 0 0 0 1 2 0 1 2 2 2 0 1 0 2 2 2 2 1 2 0 1 2 0 0 0 0 0 0 1 0 0 0 0
 2 0 2 2 2 2 2 2 0 2 1 0 0 2 2 2 2 0 2 0 2 0 2 1 1 2 1 2 1 1 1 2 2 0 0 0 0
 2]

模型效果指标评估

from sklearn import metrics # 导入sklearn效果评估模块

n_samples, n_features = X.shape # 总样本量，总特征数
print ('samples: %d \t features: %d' % (n_samples, n_features))  # 打印输出样本量和特征数量

samples: 1000 	 features: 2

评估指标1: inertias

inertias是K均值模型对象的属性，表示样本距离最近的聚类中心的总和，它是作为在没有真实分类结果标签下的非监督式评估指标。该值越小越好，值越小证明样本在类间的分布越集中，即类内的距离越小。

inertias = model_kmeans.inertia_  # 样本距离最近的聚类中心的总和
print(inertias)

300.1262936093466

评估指标2: adjusted_rand_s:，调整后的兰德指数（Adjusted Rand Index）

兰德指数通过考虑在预测和真实聚类中在相同或不同聚类中分配的所有样本对和计数对来计算两个聚类之间的相似性度量。调整后的兰德指数通过对兰德指数的调整得到独立于样本量和类别的接近于0的值，其取值范围为[-1,1]，负数代表结果不好，越接近于1越好，意味着聚类结果与真实情况越吻合。

adjusted_rand_s = metrics.adjusted_rand_score(y_true, y_pre)  # 调整后的兰德指数
print(adjusted_rand_s)

0.9642890803276076

评估指标3: mutual_info_s，互信息（Mutual Information, MI）

互信息是一个随机变量中包含的关于另一个随机变量的信息量，在这里指的是相同数据的两个标签之间的相似度的量度，结果是非负值。

mutual_info_s = metrics.mutual_info_score(y_true, y_pre)  # 互信息
print(mutual_info_s)

1.0310595406681184

评估指标4: adjusted_mutual_info_s，调整后的互信息（Adjusted Mutual Information, AMI）

调整后的互信息是对互信息评分的调整得分。它考虑到对于具有更大数量的聚类群，通常MI较高，而不管实际上是否有更多的信息共享，它通过调整聚类群的概率来纠正这种影响。当两个聚类集相同（即完全匹配）时，AMI返回值为1；随机分区（独立标签）平均预期AMI约为0，也可能为负数。

adjusted_mutual_info_s = metrics.adjusted_mutual_info_score(y_true, y_pre)  # 调整后的互信息
print(adjusted_mutual_info_s)

0.938399249349474


/anaconda3/lib/python3.6/site-packages/sklearn/metrics/cluster/supervised.py:732: FutureWarning: The behavior of AMI will change in version 0.22. To match the behavior of 'v_measure_score', AMI will use average_method='arithmetic' by default.
  FutureWarning)

评估指标5: homogeneity_s，同质化得分（Homogeneity）

如果所有的聚类都只包含属于单个类的成员的数据点，则聚类结果将满足同质性。其取值范围[0,1]值越大意味着聚类结果与真实情况越吻合。

homogeneity_s = metrics.homogeneity_score(y_true, y_pre)  # 同质化得分
print(homogeneity_s)

0.9385116928897981

评估指标6: comleteness_s，完整性得分（Completeness）

如果作为给定类的成员的所有数据点是相同集群的元素，则聚类结果满足完整性。其取值范围[0,1]值越大意味着聚类结果与真实情况越吻合。

completeness_s = metrics.completeness_score(y_true, y_pre)  # 完整性得分
print(completeness_s)

0.9385372785555511

评估指标7: v_measure_s，V-measure得分

它是同质化和完整性之间的谐波平均值，v=2*(均匀性 * 完整性)/（均匀性 + 完整性）。其取值范围[0,1],值越大意味着聚类结果与真实情况越吻合。

v_measure_s = metrics.v_measure_score(y_true, y_pre)  # V-measure得分
print(v_measure_s)

0.938524485548298

评估指标8: silhouette_s，轮廓系数（Silhouette）

它用来计算所有样本的平均轮廓系数，使用平均群内距离和每个样本的平均最近簇群距离来计算，它是一种非监督式评估指标。其最高值为1，最差值为-1，0附近的值表示重叠的聚类，负值通常表示已被分配到错误的集群。

silhouette_s = metrics.silhouette_score(X, y_pre, metric='euclidean')  # 平均轮廓系数
print(silhouette_s)

0.6342086134083013

评估指标9: calinski_harabaz_s，Calinski和Harabaz得分

该分数定义为群内离散与簇间离散的比值，它是一种非监督式评估指标。

calinski_harabaz_s = metrics.calinski_harabaz_score(X, y_pre)  # Calinski和Harabaz得分
print(calinski_harabaz_s)

2860.8215946947635

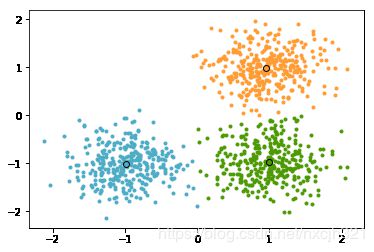
模型效果可视化

centers= model_kmeans.cluster_centers_ # 各类别中心
colors = ['#4EACC5', '#FF9C34', '#4E9A06']  # 设置不同类别的颜色
plt.figure() # 建立画布
for i in range(n_clusters):  # 循环读类别
    index_sets = np.where(y_pre == i)  # 找到相同类的索引集合
    cluster = X[index_sets]  # 将相同类的数据划分为一个聚类子集
    plt.scatter(cluster[:, 0], cluster[:, 1], c=colors[i], marker='.')  # 展示聚类子集内的样本点
    plt.plot(centers[i][0], centers[i][1], 'o', markerfacecolor=colors[i], markeredgecolor='k',
             markersize=6)  # 展示各聚类子集的中心
plt.show() # 展示图像

    

模型应用

new_X = [[1,3.6]]
cluster_label = model_kmeans.predict(new_X)
print('cluster of new data point is: %d' % cluster_label)

cluster of new data point is:  1