吴恩达机器学习-编程练习-ex2.2

1.实现sigmoid function
在开始练习实际的代价函数之前，我们先回顾一下logistic的基本假设和Sigmoid函数：

函数G即Sigmoid函数，这个Sigmoid函数的形式是：

然后我们在python中实现一下这个算法，令这个算法对单值和矩阵都生效

python中实现sigmoid函数：

import numpy as np

def sigmoid(x):
    y = 1/(1+np.exp(-x))
    return y

if __name__ == '__main__':
    # x = 0
    x = np.array([1,3,2,0])
    s = sigmoid(x)
    print(s)

输出

[0.73105858 0.95257413 0.88079708 0.5 ]

2.代价函数和梯度

我们先回顾一下代价函数的形式：

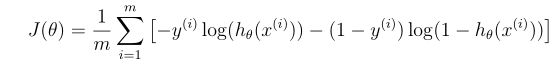
而代价函数的梯度是一个有相同θ的向量：

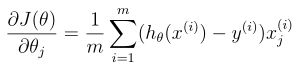
接下来我们在python中实现这两个函数，先上结果代码

import numpy as np
import sigmoid

def costFunction(theta,x,y):
    m = len(y)
    #直接用*连接两个矩阵会报错，所以我们使用numpy中的矩阵乘法函数matmul
    matmul = np.matmul(x,theta)
    h = sigmoid.sigmoid(matmul)
    #代价函数的python翻译，注意，这里原式是级数求和，但矩阵乘法的本质就是对应元素求和，所以这里矩阵相乘就相当于是矩阵求和
    #另外，注意matlab中y'相当于是y求转置，所以翻译成python就是y.T
    J = (1/m)*((np.matmul(-y.T,np.log(h))-np.matmul((1-y).T,np.log(1-h))))
    grad = (1 / m) * np.matmul(x.T,h-y)
    return J,grad

#调用数据进行验证
if __name__ == '__main__':
    path = 'C:\\Users\Administrator\PycharmProjects\Clear\ml\ex2\ex2data1.txt'
    df = np.genfromtxt(path,delimiter=',')
    #这里注意，在array中取某列采用的形式是0：2或者2：3，如果只用2取一列的话会出问题（取的是1维矩阵，另一种方法取的是2维矩阵）
    x = df[:,0:2]
    y = df[:,2:3]
    #给出矩阵的大小
    [m, n] = np.shape(x)
    #生成全1矩阵
    ones = np.ones((m,1))
    #横向拼接矩阵
    x = np.hstack((ones,x))
    #生成全0矩阵
    theta = np.zeros((3,1))
    [cost, grad] = costFunction(theta, x, y)
    print(cost,grad)

将matlab中的代码在python中实现，可以说是踩了不少坑。

需要注意的是，import sigmoid是我们刚刚写好的sigmoid function，在这里被调用。

3.模拟matlab中的fminunc优化函数

Octave / MATLAB的fminunc是一个优化求解器，可以找到无约束函数的最小值。 对于逻辑回归，我们希望使用参数θ优化成本函数J（θ）

这里偷了个懒，直接在网上找到前人的足迹，说scipy中的minimize可以进行替代。同时，该函数的参数theta一定需要是一个一维数组，引用他的描述就是

需要注意的是fun关键词参数里面的函数，需要把优化的theta放在第一个位置，X,y，放到后面。并且，theta在传入的时候一定要是一个一维shape（n,）的数组，不然会出错。
然后jac是梯度，这里的有两个地方要注意，第一个是传入的theta依然要是一个一维shape(n,)，第二个是返回的梯度也要是一个一维shape(n,)的数组。
总之，关键在于传入的theta一定要是一个1D shape(n,)的，不然就不行。我之前为了方便已经把theta塑造成了一个（n,1）的列向量，导致使用minimize时会报错。所以，学会用help看说明可谓是相当重要啊~

然后贴出实现函数的源码

import numpy as np
import pandas as pd
import scipy.optimize as op


def LoadData(filename):
    data = pd.read_csv(filename, header=None)
    data = np.array(data)
    return data


def ReshapeData(data):
    m = np.size(data, 0)
    X = data[:, 0:2]
    Y = data[:, 2]
    Y = Y.reshape((m, 1))
    return X, Y


def InitData(X):
    m, n = X.shape
    initial_theta = np.zeros(n + 1)
    VecOnes = np.ones((m, 1))
    X = np.column_stack((VecOnes, X))
    return X, initial_theta


def sigmoid(x):
    z = 1 / (1 + np.exp(-x))
    return z


def costFunction(theta, X, Y):
    m = X.shape[0]
    J = (-np.dot(Y.T, np.log(sigmoid(X.dot(theta)))) - np.dot((1 - Y).T, np.log(1 - sigmoid(X.dot(theta))))) / m
    return J


def gradient(theta, X, Y):
    m, n = X.shape
    theta = theta.reshape((n, 1))
    grad = np.dot(X.T, sigmoid(X.dot(theta)) - Y) / m
    return grad.flatten()


if __name__ == '__main__':
    data = LoadData('C:\\Users\Administrator\PycharmProjects\Clear\ml\ex2\ex2data1.txt')
    X, Y = ReshapeData(data)
    X, initial_theta = InitData(X)
    result = op.minimize(fun=costFunction, x0=initial_theta, args=(X, Y), method='TNC', jac=gradient)
    print(result)

最后结果如下，符合MATLAB里面用fminunc优化的结果（fminunc:cost:0.203,theta:-25.161,0.206,0.201）

fun: array([0.2034977])
     jac: array([8.95038682e-09, 8.16149951e-08, 4.74505693e-07])
 message: 'Local minimum reached (|pg| ~= 0)'
    nfev: 36
     nit: 17
  status: 0
 success: True
       x: array([-25.16131858,   0.20623159,   0.20147149])

4.绘制决策边界

使用优化函数计算出的theta就是决策边界的参数

#绘制决策边界
#matlab中取列1，输入1；python取列1，输入0，因为array从0开始取值
#绘制决策边界只需要两个端点
plot_x = [min(x[:,1])-2,  max(x[:,1])+2]
plot_y = (-1/theta[2])*(theta[1]*plot_x + theta[0])
scatter(X,Y,marker = '*',color = 'r')
scatter(X2,Y2,marker = '+',color = 'y')
plot(plot_x,plot_y)
show()

结果展示

符合预期的输出