曼哈顿距离最小生成树

转载请注明出处，谢谢http://blog.csdn.net/ACM_cxlove?viewmode=contents    by---cxlove

二维平面中有一些点，两点之间的距离为曼哈顿距离，求最小生成树。

朴素的n个点，只能做到O(n^3)或者O(n^2 lgn)。

但是针对这种曼哈顿距离的MST。

其中有个性质是：对于某个点，以他为中心的区域分为8个象限，对于每一个象限，只会取距离最近的一个点连边。

这样的话，由于边是双向的，所以对于每个点只需要考虑4个方向，边的数目最多为O(4*n)，再使用kruskal就可以做到O(nlgn)了。

至于证明：

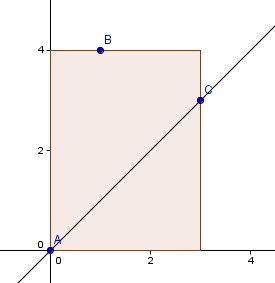
这个结论可以证明如下：假设我们以点A为原点建系，考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2)，不妨设|AB|≤|AC|（这里的距离为曼哈顿距离），如下图：

|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。下面我们分情况讨论：

1.      x1>x2且y1>y2。这与|AB|≤|AC|矛盾；

2.      x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；

3.      x1>x2且y1≤y2。与2同理；

4.      x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。

综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。

转自： http://blog.csdn.net/huzecong/article/details/8576908 

那么如果有了结论之后，怎么样筛选出每个区域最近的点

首先是8个方向，由于边的双向性，我们只需要针对一个点考虑4个方向即可。这4个方向（比如说Y轴右侧），那么都可以通过坐标变换到某一个区域，（比如说y>x）。关于y=x或者y=0对称就可以实现。

对于y>x这个区域，如果对于点A(x0,y0) 在这个区域中有个点B(x1,y1)。

那么x1>x0&&y1-x1>y0-x0。而dist(A,B)=x1-x0+y1-y0=x1+y1-(x0+y0)，那么对于点A，则是找在这个区域内x1+y1最小的点。

那么什么样的点满足在这个区域内呢，（X1>X0&&Y1-X1>Y0-X0）便 是条件

我们将坐标按X排序，将Y-X离散化，用BIT来维护，查询对于某一个X0，查询比(Y0-X0)大的中X1+Y1最小的点。

将这条边加上，重复4个区域之后，就是kruskal了。

资料：

http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=lineSweep 

题目：POJ 3241    http://poj.org/problem?id=3241

           icpcarchive 3662 https://icpcarchive.ecs.baylor.edu/index.php? option=com_onlinejudge&Itemid=8&page=show_problem&problem=1663

POJ 3241：求曼哈顿最小生成树上第K大边长度 。

#include 
#include 
#include 
#define lowbit(x) (x&(-x))
using namespace std;
const int N = 100005;
struct Point{
    int x,y,id;
    bool operator<(const Point p)const{
        return x!=p.x?x=1;i-=lowbit(i))
        if(val=0;i--){
            int pos=lower_bound(b,b+m,a[i])-b+1;   //BIT中从1开始
            int ans=ask(pos,m);
            if(ans!=-1)
                addedge(p[i].id,p[ans].id,dist(i,ans));
            update(pos,p[i].x+p[i].y,i);
        }
    }
    sort(e,e+tot);
    int cnt=n-k;
    for(int i=0;i