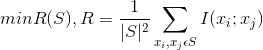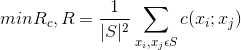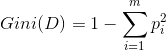【机器学习】特征选择之最小冗余最大相关性(mRMR)与随机森林(RF)

特征选择之最小冗余最大相关性(mRMR)

最小冗余最大相关性(mRMR)是一种滤波式的特征选择方法，由Peng et.al提出。主要用途有机器学习，图像识别等。

一种常用的特征选择方法是最大化特征与分类变量之间的相关度，就是选择与分类变量拥有最高相关度的前k个变量。但是，在特征选择中，单个好的特征的组合并不能增加分类器的性能，因为有可能特征之间是高度相关的，这就导致了特征变量的冗余。这就是Peng et.al说的“the m best features are not the best m features”。因此最终有了mRMR，即最大化特征与分类变量之间的相关性，而最小化特征与特征之间的相关性。这就是mRMR的核心思想。

最大相关最小冗余（mRMR），顾名思义，它不仅考虑到了特征和label之间的相关性，还考虑到了特征和特征之间的相关性。度量标准使用的是互信息(Mutual information)。对于mRMR方法，特征子集与类别的相关性通过各个特征与类别的信息增益的均值来计算，而特征与特征的冗余使用的是特征和特征之间的互信息加和再除以子集中特征个数的平方，因为I(xi,xj)计算了两次。

互信息：给定两个随机变量x和y，它们的概率密度函数（对应于连续变量）为。则互信息为

mRMR算法：找出含有个特征的特征子集S

1.离散变量

(1)最大相关性

为第i个特征，c为类别变量，S为特征子集

(2)最小冗余度

2.连续变量

(1)最大相关性

为F统计量

(2)最小冗余度

为相关函数

对于这些目标函数，还可以换成其他的函数，如信息增益、基尼系数等，然后整合最大相关性和最小冗余度：

加法整合：

乘法整合：

在实践中，用增量搜索方法寻找近似最优的特征。假设已有特征集，任务就是从剩下的特征中找到第m个特征，通过选择特征使得最大。增量算法优化下面的条件：

其算法复杂度为

mRMR算法的实现，参考github链接：https://github.com/csuldw/MachineLearning/tree/master/mRMR

算法的优点：

• 速度快
• 估计结果有较好的鲁棒性
• 是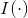的一阶最优估计

使用mRMR进行特征选择后，会得到一个重要性排名。接下来通常需要结合交叉验证来选择结果性能最好的特征子集。比较原始的方法就是，根据排名对特征子集从top1-topn一个个进行交叉验证测试，然后选择结果最好的一组特征即可。

参考资料：

1. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy
2. Feature Selection for High-Dimensional Data

特征选择之随机森林(RF)

Random Forest ：随机森林，使用的CART算法的方法增长树，也就是使用Gini指数来划分。Gini指数度量的是数据分区或训练集D的不纯度（注意，这里是不纯度，跟熵有点不同）。基尼不纯度表示的是一个随机选中的样本在子集中被分错的可能性。基尼不纯度为这个样本被选中的概率乘上它被分错的概率。当一个节点中所有样本都是一个类时，基尼不纯度为零。 定义为：

当考虑二元划分裂时，计算每个结果分区的不纯度加权和。比如A有两个值，则特征D被划分成D1和D2,这时Gini指数为：

Gini指数偏向于多值属性，并且当类的数量很大时会有困难，而且它还倾向于导致相等大小的分区和纯度。但实践效果不错。

互信息：是条件概率与后验概率的比值，化简之后就可以得到信息增益。所以说互信息其实就是信息增益。计算方法【互信息=熵-条件熵】。熵描述的是不确定性。熵越大，不确定性就越大，条件熵H（B|A）描述的是在A给定的条件下B的不确定性，如果条件熵越小，表示不确定性就越小，那么B就越容易确定结果。所以使用熵减去条件熵，就得到了信息增益，它描述的不确定性的降低程度，可以用来度量两个变量的相关性。比如，在给定一个变量的条件下，另一个变量它的不确定性能够降低多少，如果不确定性降低得越多，那么它的确定性就越大，就越容易区分，两者就越相关。

随机森林对于每一棵决策树，首先对列（特征）进行采样，然后计算当前的Gini指数，随后进行全分裂过程，每棵树的非叶节点都有一个Gini指数，一棵树建立之后可以得到该树各个节点的重要性，通过对其按照Gini指数作为特征相关性来排序，接着一次建立多棵决策树，并且生成多个特征相关性排名，最后对这些特征选平均值，得到最终排好序的特征重要性排名。

随机森林OOB特征选择：

1. 首先建立m棵决策树，然后分别计算每棵树的OOB袋外误差errOOBj。
2. 计算特征的重要性。随机的修改OOB中的每个特征的值，再次计算它的袋外误差errOOBi；
3. 按照特征的重要性排序，然后剔除后面不重要的特征；
4. 然后重复以上步骤，直到选出m个特征。

在scikit-learn中封装了random forest特征选择方法：

# -*- coding: utf-8 -*-
"""
Created on Thu Dec 13 11:35:01 2018

@author: PANG
"""

from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
import numpy as np

# load boston housing dataset as an example
boston = load_boston()
X=boston['data']
Y=boston['target']
names=boston['feature_names']
rf = RandomForestRegressor()
rf.fit(X,Y)
print("Features sorted by their score:")
print(sorted(zip(map(lambda x:round(x,4),rf.feature_importances_),names),reverse=True))

最后输出的是：