分布式游戏服务器全服匹配玩法设计
-
背景
如今的社交类游戏,大多采用分布式服务器架构,也就是说所有区服的数据存储在一个集群中,玩家可以无阻碍交互,一同游玩。
再谈游戏中的匹配,多数匹配玩法都属于在线匹配,属于非常实时的一种匹配,匹配节点会根据玩家的操作(开始匹配,报名, 匹配完成等) 动态插入删除。这也就保证了匹配池的节点数量会维持在可控的范围内。
而如果游戏中有海量的小团体, 要求每隔一定周期为全服所有团体分配一个实力相近的对手, 应该如何高效实现这个需求呢?
-
需求分析
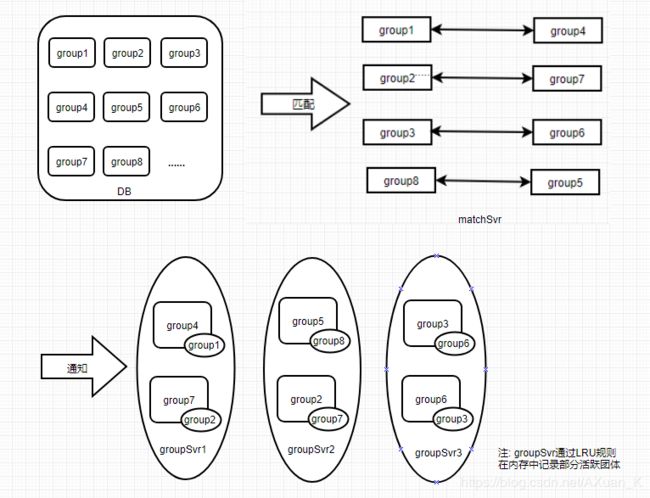
根据需求描述,结合现有的团体功能在服务器中的架构,系统所需要完成的功能如下图所示:
简而言之,我们需要通过一定的规则把游戏中的所有团体两两匹配在一起,然后逐一通知自己的匹配结果。
对于海量数据节点的匹配,很显然内存中已经无法存下所有节点了。最直观的解决方案就是将所有匹配节点的关键信息存储在DB中,到达匹配开始时间后再每次获取一批匹配节点分批进行匹配。
确定好大致方向,接下来需要解决如下五个问题:
- 如何维护匹配节点
- 如何分批匹配
- 在何处进行匹配
- 匹配规则的具体实现
- 如何分发匹配信息
-
数据维护
匹配节点的维护很简单:因为匹配的范围是全服所有团体,很容易想到匹配节点的生命周期和对应团体是绑定在一起的,即
- 团体达到玩法开启等级插入一条匹配节点记录;
- 团体解散删除这条记录;
- 节点中关键字段变化更新记录;
值得一提的是,匹配节点的更新可以通过增加脏标记的方式,控制频率固定时间间隔更新, 这样可以避免其他业务代码影响到匹配系统的整体压力。
-
分批匹配
分批匹配,最重要的就是解决分批获取表格中全量数据问题,常见的做法有两种:
1. 遍历表格,按固定顺序固定数量获取数据依次匹配。
2.自定义哈希规则为每个团体分配一个额外的值随机的key, 对这个key建立索引,最后每批选择其中一部分key进行拉取。
表格遍历是最简单有效的方案,可以完成基本需求,但会面临两个小问题:由于是固定顺序固定数量下的分批匹配,每轮匹配的分组大致是固定的,这也就意味着极限情况下,可能出现多轮匹配到相同对手的情况。
另外,表格遍历数据返回的方式是单向通知,而不是主动拉取的。考虑到匹配是一个非常占用CPU时间的操作,在匹配节点非常多的情况下,前一批节点还在占用CPU进行匹配中而后面几批节点已经返回,从而导致缓冲区占满而丢失部分消息。
第二种方法实际上就是通过part key进行批量拉取,先不谈BatchGetByPartKey这个操作本身很低效,虽然解决了遍历表格出现的两种问题,但极度依赖哈希算法,随着节点数量的增加,key的数量也需要随之增加,也就是说哈希算法需要做到随着节点数量的增加动态变更,流程代码实现也将变得复杂,整体很不灵活而且低效。
那么有没有一种分批拉取策略既可以结合两者优势呢,又可以避免两者已存在的坑呢?
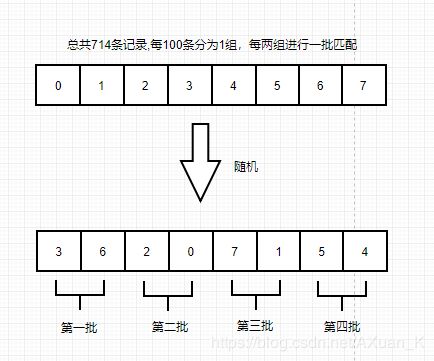
仔细斟酌,实际上我们需要的是一种可以随机顺序主动拉取的遍历表格方式。如果可以打乱整张匹配节点表格,再进行遍历拉取一切就很好办了,但如果想在内存中存下整张表格随机后的顺序则需要耗费大量的空间。 考虑一个折中的方案: 将整张表格的所有节点分成固定数量的X组,再将这些分组采用O(N)洗牌算法打乱, 最后每批拉取Y组进行匹配。这样,在内存中我们仅需存下分组的顺序以及当前拉取的进度即可。
有一点值得注意的是, 因为采用的是设置下标的分批拉取,在拉取期间如果发生了节点删除,拉取后续节点可能出现遗漏的情况;故如果在匹配期间发生了团体解散,我们需要记录并延迟删除。
至于具体的实现: 我们可以给所有匹配节点分配一个额外的值相同的key,在每组数据拉取的时候采用TCAPLUS_API_GET_BY_PARTKEY_REQ接口, 根据组号设置offset和limit,本批所有分组拉取完成则开始匹配。
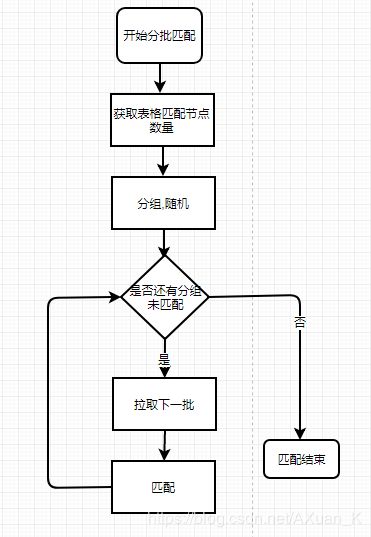
整个分批匹配的流程如下:
-
系统容灾
在何处匹配,本质上就是解决匹配系统的容灾问题。
选择在何处匹配,最简单直观的方案,就是为其增加一个负责匹配的单点进程,伴随而来的问题也非常明显:代码工程量加大,其次添加单点进程并不符合分布式系统功能设计的基本思想,增加单点匹配进程的方案先被否决。
那么我们能否用现有的团体服务器groupSvr进行匹配呢?团体服务器本身是支持动态增删的, 且服务器本身存在机器故障,进程宕机的可能性,选择某个固定的团体服务器进程进行匹配并不合理。
那么如何动态选择某个团体服务器进行匹配呢? 这里我们可以采用多个进程抢占乐观锁的方式争夺匹配权,保证同一时间只有其中一个进程进行全服匹配;同时需要增加超时处理机制,当某个进程正在匹配中,发生了宕机导致匹配超时,会有其他进程继续抢占乐观锁将匹配流程进行下去。进程抢占匹配权流程如下:
由于匹配进程存在中途宕机的可能,分批匹配的过程中我们需要在<分组,随机>步骤和<匹配>步骤完成后及时将分组顺序,匹配进度,上批匹配完成时间等信息存入DB,保证异常情况匹配流程能够顺利进行下去。
-
规则实现
接下来需要思考的是匹配系统最核心的部分,如何在每批匹配节点中,撮合尽可能多的实力相近的对手。
首先简单转化/翻译一下策划定义的匹配规则:
- 匹配节点包含多个字段,当两个节点相同字段差值在某指定范围内的话,则定义为实力相近的对手,允许匹配在一起。
- 当一轮匹配执行完后,如果仍剩下未匹配的节点,则对差值范围进行扩大,继续下一轮匹配。
- 多轮阔段匹配后仍有剩余节点,将剩余节点再按综合能力值排序,进行保底匹配。
如何实现上述规则呢? 我们仍然从最简单最直观的方案出发:
- 每轮遍历所有节点,当发现两个节点可匹配的话,则将这两个节点从匹配池中删除;
- 对于多轮匹配,它们的区别仅仅是字段的差值范围不同(保底匹配的差值范围为无限大);
这样, 我们可以将一批节点进行匹配的流程抽象如下:
struct MatchNode{};
struct MatchGap;
class CGroupMatchProcessor
{
public:
//开始本批匹配
void StartMatch()
{
std::sort(nodeList.begin(), nodeList.end());
//step1
MatchProcess(MatchConfig::GetBaseGap());
//step2
for(int i = 0; i < MatchConfig::GetExpandCnt(); ++i)
{
MatchProcess(MatchConfig::GetExpandGap(i));
}
//step3
MatchProcess(MatchConfig::GetFinalGap());
}
private:
void OnMatchDone(const MatchNode& stNode1, const MatchNode& stNode2);
bool IsMatch(const MatchNode& stNode1, const MatchNode& stNode2, const MatchGap& stGap);
//进行一轮匹配
void MatchProcess(const MatchGap& stGap)
{
for(size_t i = 0; i < nodeList.size(); ++i)
{
for(size_t j = i + 1; j< nodeList.size(); ++j)
{
if(IsMatch(nodeList[i], nodeList[j], stGap))
{
OnMatchDone(nodeList[i], nodeList[j]);
OnMatchDone(nodeList[j], nodeList[i]);
nodeList.erase(nodeList.begin() + j);
nodeList.erase(nodeList.begin() + i);
i -= 1;
break;
}
}
}
}
private:
std::vector nodeList;
};
匹配过程的核心代码为MatchProcess函数,整体实现比较简单。但测试过几组数据之后,发现这个算法并不能完成"撮合尽可能多的实力相近的对手"这一要求,而且因为存在频繁的内存移动,匹配效率也令人堪忧。
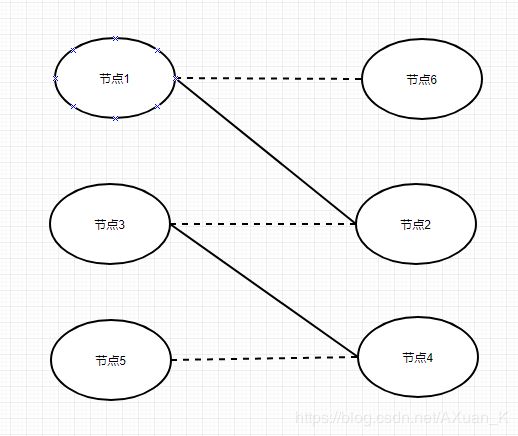
无法完成要求的例子见下图, 其中虚线代表两节点允许相互匹配,实线代表已完成的匹配:
图中的例子,最理想的情况是能撮合出三组匹配,但由于<节点1,节点2>, <节点3,节点4>已完成匹配并删除,所以导致最终只撮合了其中两组。究其原因,还是因为算法的本质仅仅是一种非常"短视"的不考虑全局其他节点的贪心选择。
那么有没有可以解决这一问题并且效率也足够高的算法呢?
大学学过图论的同学可能听说过,匈牙利数学家曾经提出过一种在多项式时间内求解任务分配问题的组合优化算法,该算法可以解决二分图的最大匹配问题,这不刚好就是我们需要的吗,于是参考算法思路改进后代码如下:
class CGroupMatchProcessor
{
public:
void StartMatch();
private:
void OnMatchDone(const MatchNode& stNode1, const MatchNode& stNode2);
bool IsMatch(const MatchNode& stNode1, const MatchNode& stNode2, const MatchGap& stGap);
//构建邻接表
void BuildGraph(const MatchGap& stGap)
{
edgeList.resize(nodeList.size());
edgeList.clear();
for(size_t i = 0; i < nodeList.size(); ++i)
{
for(size_t j = i + 1; j< nodeList.size(); ++j)
{
if(IsMatch(nodeList[i], nodeList[j], stGap))
{
edgeList[i].push_back(j);
edgeList[j].push_back(i);
}
}
}
}
//寻找增广路
bool FindPath(int u)
{
std::vector& edgeTo = edgeList[u];
for(size_t i = 0; i remainList;
remainList.clear();
for(size_t i = 0; i < nodeList.size(); ++i)
{
if(matchPeer[i] == -1)
{
remainList.push_back(nodeList[i]);
}
else
{
OnMatchDone(nodeList[i], nodeList[matchPeer[i]]);
}
}
nodeList.swap(remainList);
}
private:
std::vector nodeList;
std::vector matchPeer;
std::set visitNodeSet;
std::vector< std::vector > edgeList;
};
如果说遍历删除属于一种短视的贪心算法,那么匈牙利算法则是一种更有远见的可以补救短视的贪心算法。
在介绍匈牙利算法之前,首先介绍两个重要的名词:
- 交错路 :从一个未匹配点出发,依次遍历未匹配边、匹配边、未匹配边,这样交替下去,这条路径称为交错路。
- 增广路 :从一个未匹配点出发,依次遍历未匹配边、匹配边、未匹配边,这样交替下去,如果最后一个点是未匹配点,这条路径称为增广路。换句话说,起点和终点都为未匹配点的交错路为增广路。
匈牙利算法的核心思想就是为图中每个未匹配节点寻找一次增广路,然后再对已有匹配关系进行替换。我们仍以上一张图举例:
- <节点1,节点2>, <节点3,节点4>这两组节点已经建立匹配关系,节点5开始寻找增广路。
- (5)首先找到(4), 而(4)已有匹配关系,然后尝试为(4)的匹配节点(3)寻找新的匹配节点,从而让(5)和(4)匹配。
- (3)找到新的可匹配节点(2),但(2)已有匹配关系,为(2)的匹配节点(1)寻找新的匹配节点,从而让(3)和(2)匹配。
- (1)找到可匹配但是未被匹配的(6),至此,增广路寻找完成。
- 最后,更换匹配关系, 即上图中的实线变为虚线, 虚线变为实线,完成三组匹配。
对于匹配规则的更高效实现,可以自行了解一下Hopcroft-Carp算法,本质是可以同时寻找出多条增广路,在这里不展开讲。
-
匹配分发
匹配的最终目标,就是需要告知每个团体自己本轮的匹配结果,将匹配结果写入团体数据中。 为了保证数据一致性,写某团体数据必须在指定的为其分配的团体服务器上进行。当一个团体服务器进程分配满后, 收到一条未在内存中团体的写请求,这时进程会触发LRU,淘汰掉其中一个并将本团体导入内存执行写操作。
考虑到全服匹配会为全服所有团体分配一个对手,这样每个团体都需要在匹配期间写一次匹配信息,而内存中只会存部分活跃团体,当大量非活跃团体匹配完成需要写匹配信息时,会造成进程的频繁LRU影响性能。
为了避免这种性能消耗,我们在匹配分发时采用写增量事件机制(eventlog)。 即匹配完成,为对应团体写一份增量事件,写入成功,通知对应团体拉取增量事件, 接下来可能会出现两种情况:
- 团体在内存中, 直接拉取增量事件;
- 团体不在内存中,忽略本次通知,等待团体导入内存再拉取增量事件;
经过改动后,成功分散了匹配分发过程中的系统压力,同时 匹配完成->收到匹配信息 不再具有连续性(可能时间差非常大),因此我们需要在增量事件中记录一个匹配完成时间,当匹配完成时间属于本轮匹配才允许记录匹配信息,否则丢弃。 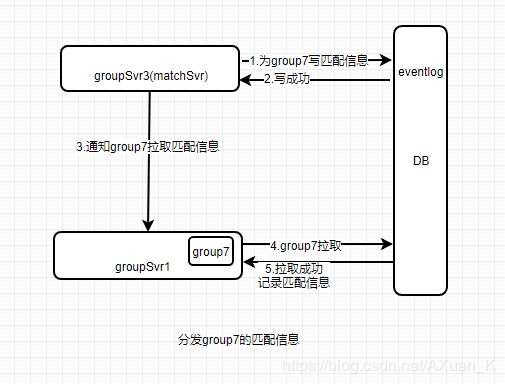
至此, 全服匹配的所有设计细节已经介绍完毕。
-
结语
受限于随机分组分批进行匹配,每批最后完成的几组匹配存在不确定性。
对于整体匹配度要求更高的匹配,可以根据匹配节点综合能力值在DB中构建一张持久化排行榜,在每期开始匹配之前生成一份排行榜快照,最后再根据快照顺序依次分批拉取分批匹配。另外,针对多期匹配节点相同的情况,我们可以将前几期的对手信息记录在匹配节点中,在构建邻接表的时候进行过滤,从而避免重复匹配到相同节点。