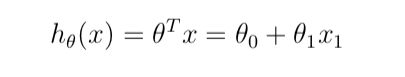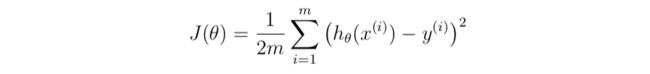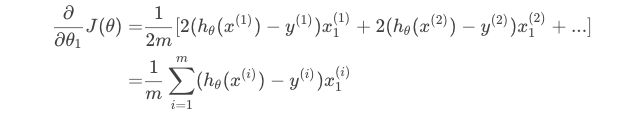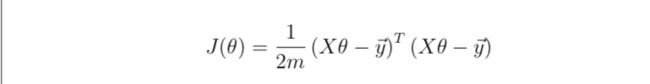吴恩达机器学习第一次编程作业----LinearRegression
1:Simple Octave/MATLAB function
第一个任务是输出一个5*5的单位矩阵,这个只需要在warmUpExercise.m文件里面添加 A = eye(5) 即可。 输出结果如下图:
A = eye(5)
1.1 Submitting Solutions
这个是讲如何提交文件的,如果是在coursea上面看课程的同学就可以提交,如果在网易云课堂里面看的应该就不行。具体略。
2:Linear regression with one variable
1:首先需要读取作业里面已经准备好的数据集(确保你的 Octave 运行在 ex1 目录下):
data = load('ex1data1.txt') % 读取ex1data1里面的数据,数据的第一列是X的值,第二列是Y的值;
X = data(:,1); y = data(:,2);
m = length(X);
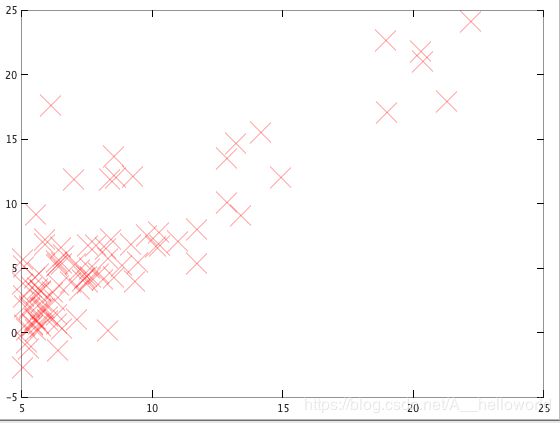
接下来,把X,Y以图像的形式表示出来:
plot(x, y, 'rx', 'MarkerSize', 10); % ‘rx’ 这里的r代表红色,x代表cross,也就是叉
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
如下图:
2.2 Gradient Descent
在作业中,我们使用的预测函数如下:
linear regression 的 cost function表示如下:
这里是用平方法来表示误差,误差越小,代表线拟合得越好,所以我们得求出使得J最小的theta的值。用梯度下降法来解决。
首先对该式子分别对 theta0 和 theta1求偏导:
对theta0:
对theta1:
对微积分知识不太熟的同学还是去看看高数书。
所以:
对于 theta0: (这里的J = 0)
对于 theta1: (这里的J = 1)
接下来是具体的实现:
X = [ones(m, 1), data(:,1)]; % X 的第一列之所以设置为1,是因为theta0没有与x相乘,所以设置为1,让矩阵相乘之后还是等于 theta0;
theta = zeros(2, 1); % initialize fitting parameters,这里可以随意设置 theta 的初始值
iterations = 1500;
alpha = 0.01;
然后打开computeCost.m文件
完成计算 cost 的代码:
J = sum((X*theta-y).^2)/(2*m);
再接下来,完成gradientDescent.m 文件里面的代码:
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s = theta;
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
theta(1) = theta(1) - alpha*sum(X*theta_s-y)/m;
theta(2) = theta(2) - alpha*sum((X*theta_s-y).*X(:,2))/m;
theta_s = theta;
注意:theta的在计算过程中会变化,所以需要用一个 theta_s = theta 来暂存上一次的计算结果。
之所以是 theta(1)和 theta(2) 而不是 theta(0)和 theta(1) 是因为 Octave 的下标是从1开始的。
然后在Octave里面调用 gradientDescent.m里面的函数:
[theta, J_history] = gradientDescent(X,y,theta,alpha,iterations)
输出J_history可以看到J的值不断变小。大家可以增加迭代的次数试试看,后面就会趋向一个稳定值。
接下来输出预测的直线:
hold on;
plot(X(:,2), X*theta, '-')
hold off
2.4 Visualizing J(θ)
下面是在一个3D的空间可视化J,下面代码不难看懂,就不再解释了。
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
J vals = zeros(length(theta0 vals), length(theta1 vals));
% Fill out J vals
for i = 1:length(theta0 vals)
for j = 1:length(theta1 vals)
t = [theta0 vals(i); theta1 vals(j)];
J vals(i,j) = computeCost(x, y, t);
end end
J_vals = J_vals';
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
获得的图像如下:
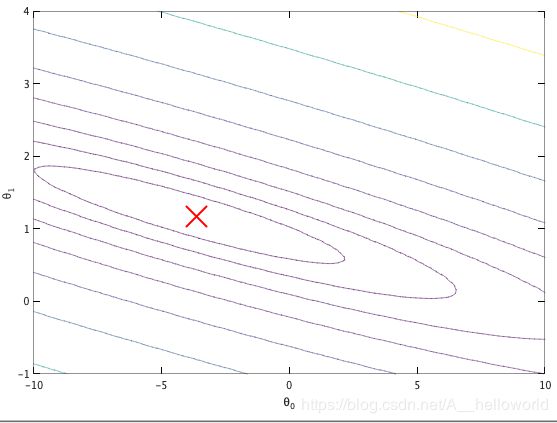
再下来获得等高线的图:
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
结果如图所示:
3 Linear regression with multiple variables
首先还是先读取数据:
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
这里看一下X,可以发现两个feature的数量级差距有点大,这样会导致在做梯度下降的时候,需要很多次的迭代才能找到最优解,所以这里最好先对数据特性归一化处理。公式如下:
PS:其中,μ是平均数,在octave里面可以通过 mean()函数求得;
σ是代表数据的标准偏移量,可以使用 std()函数求得,具体的公式可以通过 help std去查看下;
3.1 Feature Normalization
下面开始完成featureNormalize.m文件:
mu = mean(X);
sigma = std(X);
X_norm = (X - repmat(mu, size(X,1), 1)) ./ repmat(sigma, size(X,1), 1);
PS: repmat() 函数可以去help一下。
下面继续:
[X mu sigma] = featureNormalize(X);
X = [ones(m,1) X] % theta0的对应的x(i)为1,也可以理解成没有x(i),这里为了计算,所以加上去
alpha = 0.01;
iterations = 400;
theta = zeros(3, 1);
另外,也要完成代价函数里面的代码,这里有两种方法,一种还是跟上面一样,另外一种是通过矩阵的运算去计算,公式如下:
J = (X*theta - y)'*(X*theta -y)/(2*m)
熟悉线性代数的理解起来不难。
3.2 Gradient Descent
接下来就是完成梯度下降函数了,这里跟上面单变量有点不太一样,上面是列举的方法计算,这里使用矩阵运算,熟悉线性代数理解起来也是不难。
theta = theta -alpha / m * X' * (X * theta -y);
接下来就是使用梯度下降来计算最优解了,然后画图:
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
%然后画图
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
3.3 Normal Equations
最后一种解法,就是使用正规方程去解,公式如下:
theta = (pinv(X'*X))*X'*y;