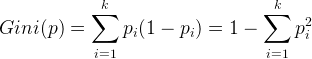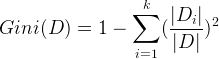决策树—分类

核心：特征选择+剪枝。

1 概述

决策树采取了“分而治之”的思想，是一种基本的分类方法，也可以用于回归。包括3个步骤：特征选择、决策树的生成和决策树的修剪。主要有ID3、C4.5和CART三种算法。

从形式上，决策树就是一棵按照各个特征建立的树形结构，叶节点表示对于的类别，特征选择的顺序不同，得到的树的形状也不同。我们追求的是模型简单、效果好，直观上也就是建立的决策树深度越小越好。

[例]（来自：李航《统计学习方法》）

下表是一个贷款统计数据（训练数据），数据中贷款申请人有4个特征：年龄、是否有工作、是否有自己的房子、信贷情况。现要通过此数据表建立一个决策树模型，用以对新的贷款申请人进行分类，来决定是否同意其贷款。        

编 号	年 龄	有工作	有自己的房子	信贷情况	是否同意(类别)
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

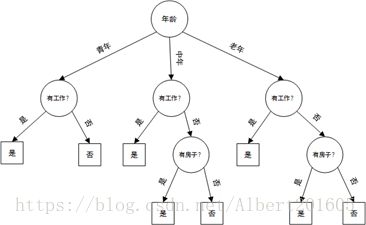
可以这样做：先看年龄（根节点），再看工作-房子-信贷，得到的决策树为

                                       

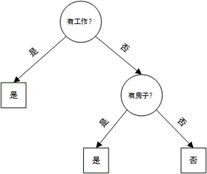
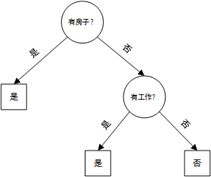
也可以这样做：按照工作-房子-年龄-信贷的顺序来看，得到的决策树如下

                                                         

可以看到，选择不同的特征顺序会得到不同的树形结构，显然第二种方法得到的决策树更简单，分类效率更高。那么到底该怎样选择特征更好呢？直观上，如果一个特征在当前条件下具有最好的分类能力，那么就应该选择这个特征。这一准则如何定量描述呢？有三种方式：信息增益、信息增益率、基尼指数，分别对应的决策树分类算法为ID3、C4.5、CART（三者的不同之处就是特征选择准则，算法思路没有差异）。

2 划分特征选择

2.1 信息增益

特征A对训练数据集D的信息增益定义为D的信息熵与A条件下的条件熵之差，即

                                                             

其中，为类别数，，为特征A的取值个数。

（信息熵参考：https://blog.csdn.net/Albert201605/article/details/81427658）

熵是随机变量不确定性的度量，根据上式，信息增益表示的是给定一个特征条件下，原数据集不确定度的缩减量，也就是特征A对数据集不确定性的消除程度，反映了其分类能力（其实也就是D与A的互信息，即数据集D中含有的特征A的信息量）。信息增益准则偏向于选择取值较多的特征（如上例中以编号作为选取特征，则g(D,编号)=H(D)有最大值）。

2.2 信息增益率

特征A对训练数据集D的信息增益率定义为其信息增益与数据集D关于特征A的取值的熵之比，即

                                                          

其中，为特征的取值个数。

2.3 基尼指数

(I). 分类问题中，假设有k个类，样本点属于第i类的概率为，则概率分布的基尼指数定义为

                                                   

对于二类分类问题，若样本点属于第1个类的概率是p，则概率分布的基尼指数为

(II). 对于给定的样本集合D，其基尼指数为

                                                  

其中，是D中属于第i类的样本集合，是类的个数。

(III) 如果样本集合D根据特征A是否取某一可能值被分割成 和 两部分，即

                                          

则在特征A的条件下，集合D的基尼指数定义为

                                   

基尼指数表示集合D的不确定性，基尼指数表示经 分割后集合D的不确定性。基尼指数越大，集合样本的不确定性也就越大，这点与熵相似。

[例]

以ID3算法对上例数据建立决策树，也就是以信息增益作为特征选择准则，做法如下：

1) 根节点选择：

                             

                            

                           

                同理，， 

由于特征的信息增益最大，所以选择作为根节点，易知取“是”时(子集)只有同一类样本点，为叶节点。

2)接着对取“否”时(子集)计算信息增益，选择第二层节点：

                           

                           

                           

选择信息增益最大的特征(有工作) 为特征节点，易知当取“是”或“否”时，样本都属于同一类，所以就是两个叶节点。

这样，生成的一棵决策树为

                                                  

3 剪枝

上面的例子中只有树的生成，对训练数据有很精确的分类效果，但分支太多了就容易过拟合，所以需要进行剪枝(pruning)处理。剪枝策略有“预剪枝”和“后剪枝”。

a. 预剪枝

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点。

至于性能的判断有不同的评估方法，如采用留出法（预留一部分数据作验证集），就是每划分一个结点前都计算划分前划分后的验证集准确率，如果准确率提高了就划分，否则就不划分。

• 优点：降低了过拟合风险，减少了训练时间和测试时间开销。
• 缺点：欠拟合风险。

b. 后剪枝

后剪枝是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

如性能评估采用留出法，就是对一棵已建立的决策树，自底向上对每棵子树进行判断：将该结点替换为叶结点（归为训练集中样本最多的类别），在验证集上的准确率是否提升？若提升则剪之；反之不剪。

后剪枝更一般化的评估方法是极小化决策树整体损失函数，其中表示模型对训练数据的预测误差，表示模型复杂度，参数控制两者之间的影响。较大偏向于使模型简化；较小则偏向于使训练集误差减小，即和训练集拟合程度高，模型越复杂（李航《统计学习方法》）。

• 优点：欠拟合风险小，泛化能力优于预剪枝。

• 缺点：训练时间开销大。

4 连续值与缺失值处理

4.1 连续值处理：二分法

前面的例子中各属性都是离散的，在一些其他问题中可能会出现连续的属性，即该特征取值为连续型随机变量，一种简单的处理方法是二分法。顾名思义，二分法就是在该连续属性中找一个点一分为二，大的一个分支，小的一个分支。

在训练集D中，假定连续属性a共有n个不同的取值，将这些值从小到大进行排序，记为.一个划分点t可将D分为两部分，一部分是不大于t的样本，记为；一部分是大于t的样本，记为. 我们把每个小区间的中位点作为候选划分点，只要在这n-1个点中找到一个最优的即可，也就是要找到一个使得信息增益最大的划分点，需满足：

              

其中是训练集D基于划分点t二分后的信息增益，即。

需注意的是，与离散属性不同，若当前结点划分属性为连续属性，该属性仍可作为其后代结点的划分属性（如父结点使用“密度>0.381”，子结点也可能使用“密度>0.563”）.

4.2 缺失值处理

为有效利用现有的数据样本，需要对一些属性缺失的样本进行处理。显然对要建立的决策树，面临的两个问题是(1)如何进行划分特征的选择？(2)若属性缺失，如何对样本划分？这里先对训练集中每个样本赋予一个权重，并全部初始化为1.

a. 特征选择：信息增益加权

既然有的样本属性缺失，那我们就按那些不缺失的计算出信息增益，再按样本比例赋上一个权重。可描述为：在训练集D中，D’为属性a上没有缺失值的样本子集，则该属性的信息增益为，其中.

b. 样本划分：加权划分

若样本x在该属性不缺失，则将其划入对应的子结点，且样本权值在子结点中保持为不变。若样本x在该属性缺失，则将其以权值同时划分到所有子结点。其中比值表示无缺失值样本中取某一属性值的样本所占比例.

pdf下载

参考

1. 李航. 《统计学习方法》
2. 周志华. 《机器学习》
3. 郑捷. 《机器学习算法原理与编程实践》
4. Thomas M.Cover. 《信息论基础》.